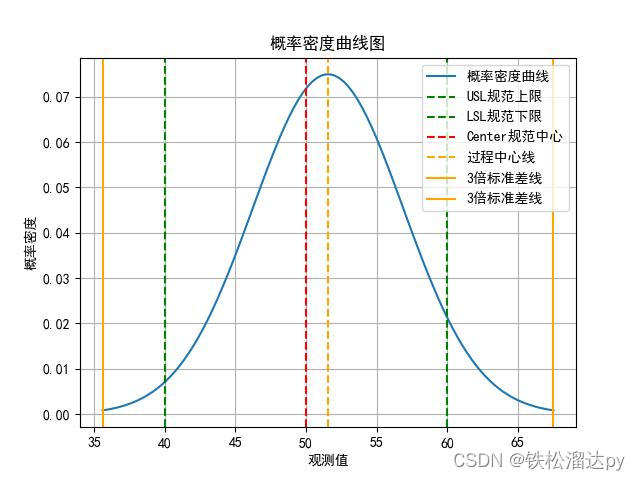
CPK（过程能力指数）是一个用于衡量一个过程的稳定性和一致性的统计指标，特别用于制造业和质量管理中。它衡量了一个过程的变异性与规范界限的关系，帮助确定过程是否能够产生合格的产品或服务。

正态分布假设：CPK的计算通常基于正态分布（或近似正态分布）的假设。这意味着过程数据应该呈现出类似正态分布的特征。如果数据不服从正态分布，可能需要进行转换或采用其他方法来处理。 

CPK 的计算涉及以下步骤：

1. 确定规范上限（USL）和规范下限（LSL）：这是产品或过程的规范要求。USL 表示规范上限，LSL 表示规范下限。

2. 计算过程的标准偏差（σ）：标准偏差是过程数据的统计度量，它表示数据的离散程度。你需要收集足够的过程数据样本，然后计算标准偏差。

3. 计算 CPK：CPK 的计算公式如下：

   CPK = min((USL - μ) / (3σ), (μ - LSL) / (3σ))

   其中：

   • USL 是规范上限
   • LSL 是规范下限
   • μ 是过程的均值
   • σ 是过程的标准偏差

CPK 值的计算结合了过程的均值、标准偏差以及规范上限（USL）和规范下限（LSL），它用于标准化地衡量一个过程的能力以产生在规格要求范围内的产品。以下是对CPK的解释的详细说明：

1. 过程均值（Mean）：CPK 考虑了过程的均值，即过程数据的平均值。均值反映了过程的中心位置，即过程在规格要求范围内的对准程度。如果均值与规格中心接近，CPK 值可能较高，表示过程接近规格要求。

2. 标准偏差（Standard Deviation）：标准偏差衡量了过程数据的变异性。它表示了过程的离散程度，即数据点在均值周围的分布程度。CPK 考虑了标准偏差，因为过程的变异性直接影响产品是否在规格要求范围内。

3. 规范上限（USL）和规范下限（LSL）：USL 表示产品在某个方面的最大允许值，LSL 表示最小允许值。CPK 的计算将这两个规格限制与过程均值和标准偏差相结合，以确定过程能否生产满足规格要求的产品。

4. 标准化度量：CPK 的计算通过将 (USL - Mean) 和 (Mean - LSL) 分别除以 (3 * Standard Deviation)，将这两个偏差标准化为标准偏差的单位。这个标准化过程允许将不同过程的能力进行比较，并且以一种标准化的方式表示。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.integrate import quad  # Import the quad function for integration

plt.rcParams['font.sans-serif'] = ['SimHei']  # 防止中文标签乱码
plt.rcParams['axes.unicode_minus'] = False
# 生成一个示例数据集，这里使用随机数据
np.random.seed(0)
data = np.random.normal(loc=50, scale=5, size=40)  # 均值=50，标准差=5

# 规范上限和规范下限，这里只是示例值，你需要根据实际情况提供
USL = 60  # 规范上限
LSL = 40  # 规范下限

# 计算均值和标准偏差
mean = np.mean(data)
std_dev = np.std(data)
Us_Ls_Center = (USL+LSL)/2

# 计算 CPK
cpk = min((USL - mean) / (3 * std_dev), (mean - LSL) / (3 * std_dev))
print("均值:", mean)
print("标准偏差:", std_dev)
print("CPK:", cpk)
# 计算规范上限和规范下限之间的合格率
acceptance_rate = norm.cdf(USL, loc=mean, scale=std_dev) - norm.cdf(LSL, loc=mean, scale=std_dev)
print("合格率:", acceptance_rate)

cp= (USL-LSL) / (6*std_dev) # 规格范围相对于过程的变异性有多宽
print("CP:", cp)

# 创建概率密度曲线的 x 值范围
x = np.linspace(mean - 3 * std_dev, mean + 3 * std_dev, 100)

# 计算概率密度函数的值
pdf = norm.pdf(x, loc=mean, scale=std_dev)


# 计算规范上限和规范下限之间的合格率
def pdf_function(x):
    return norm.pdf(x, loc=mean, scale=std_dev)
def calculate_acceptance_rate(pdf_func, LSL, USL):
    area, _ = quad(pdf_func, LSL, USL)
    return area
acceptance_rate = calculate_acceptance_rate(pdf_function, LSL, USL)
print("合格率:", acceptance_rate)


# 绘制概率密度曲线图
plt.plot(x, pdf, label='概率密度曲线')
plt.xlabel('观测值')
plt.ylabel('概率密度')
plt.title('概率密度曲线图')

# 添加规范上限、规范下限、规格中心线和3倍标准差线
plt.axvline(x=USL, color='g', linestyle='--', label='USL规范上限')
plt.axvline(x=LSL, color='g', linestyle='--', label='LSL规范下限')
plt.axvline(x=Us_Ls_Center, color='r', linestyle='--', label='Center规范中心')
plt.axvline(x=mean, color='orange', linestyle='--', label='过程中心线')
plt.axvline(x=mean + 3 * std_dev, color='orange', linestyle='-', label='3倍标准差线')
plt.axvline(x=mean - 3 * std_dev, color='orange', linestyle='-',label='3倍标准差线')

plt.legend()
plt.grid(True)

# 显示图形
plt.show()

 

CPK 和 CP 都是用于衡量过程能力的指标，它们在质量管理和质量控制领域经常被使用，但它们有不同的计算方法和用途：

1. CP（过程能力指数）：

   • CP 表示过程能力指数，它用于衡量一个过程的能力，以产生在规格上限（USL）和规格下限（LSL）之间的产品。
   • CP 的计算公式为：CP = (USL - LSL) / (6σ)，其中 USL 表示规格上限，LSL 表示规格下限，σ 表示过程的标准偏差。
   • CP 的值告诉我们规格范围相对于过程的变异性有多宽，但它不考虑过程的偏差（均值与规格中心的偏离）。

2. CPK（过程能力指数修正版）：

   • CPK 也用于衡量过程的能力，但相对于 CP，它考虑了过程的偏差。
   • CPK 的计算公式为：CPK = min((USL - Mean) / (3σ), (Mean - LSL) / (3σ))，其中 USL 表示规格上限，LSL 表示规格下限，σ 表示过程的标准偏差，Mean 表示过程的均值。
   • CPK 考虑了过程的偏差，并告诉我们过程的能力，以产生在规格上限和规格下限之间的产品。CPK 值越大，表示过程的能力越高，因为它同时考虑了规格要求和过程的变异性。

要点总结：

• CP 衡量规格范围相对于过程变异性的宽度。
• CPK 同时考虑规格范围、过程变异性和过程偏差。
• CPK 是更全面和常用的过程能力指数，因为它提供了更多信息，特别是对于那些偏差较大的过程。在质量管理中，通常更关注 CPK 值。

 绘制X-bar图

import numpy as np
import matplotlib.pyplot as plt

# 示例数据，包含10个子组的样本数据，每个子组有5个样本
data = np.array([
    [10, 12, 11, 9, 17],
    [14, 15, 13, 11, 12],
    [10, 9, 11, 12, 10],
    [12, 11, 10, 12, 11],
    [9, 11, 22, 4, 12],
    [11, 10, 15, 10, 11],
    [13, 12, 11, 12, 14],
    [10, 9, 11, 12, 10],
    [12, 4, 34, 12, 11],
    [9, 11, 10, 9, 12]
])

# 计算每个子组的平均值和范围
subgroup_Xmeans = np.mean(data, axis=1)  # 计算每个子组的平均值
subgroup_Rranges = np.ptp(data, axis=1)  # 计算每个子组的范围（即极差）

# 计算总体平均值
overall_Xmean = np.mean(subgroup_Xmeans)  # 所有子组平均值的平均值，表示整体过程的中心位置。它是X-bar图中的中心线。
overall_Rmean = np.mean(subgroup_Rranges)  # 所有子组的极差的平均值，表示整体过程的离散程度

# 计算A2、D3和D4常数（这里假设样本大小为5，您可以根据实际情况修改）
A2 = 0.577
D3 = 0
D4 = 2.114

# 计算控制限
UCL_X = overall_Xmean + A2 * overall_Rmean
LCL_X = overall_Xmean - A2 * overall_Rmean

UCLR = D4 * overall_Rmean
LCLR = D3 * overall_Rmean

# 计算R控制图的控制限（使用D4常数）
UCL_R = UCLR
LCL_R = LCLR

# 计算每个子组的Z分数
z_scores = (subgroup_Xmeans - overall_Xmean) / (overall_Rmean / np.sqrt(data.shape[1]))

# 设置阈值，通常选择2或3作为阈值
threshold = 3

# 异常检测并标记异常点
plt.figure(figsize=(6, 9))
plt.subplot(2, 1, 1)
plt.plot(subgroup_Xmeans, marker='o', linestyle='-')
plt.axhline(y=overall_Xmean, color='r', linestyle='--', label='Overall Xmean')
plt.axhline(y=UCL_X, color='g', linestyle='--', label='UCL')
plt.axhline(y=LCL_X, color='g', linestyle='--', label='LCL')
plt.legend()
plt.title('X-bar')
plt.xlabel('Subgroup')
plt.ylabel('Subgroup Mean')

# 异常检测 - 使用Z分数
outliers = np.where(np.abs(z_scores) > threshold)[0]
for o in outliers:
    plt.annotate(f'Outlier (Subgroup {o+1})', (o, subgroup_Xmeans[o]), textcoords="offset points", xytext=(0,10), ha='center')

# 绘制R控制图
plt.subplot(2, 1, 2)
plt.plot(subgroup_Rranges, marker='o', linestyle='-')
plt.axhline(y=overall_Rmean, color='r', linestyle='--', label='Overall Rmean')
plt.axhline(y=UCL_R, color='g', linestyle='--', label='UCL')
plt.axhline(y=LCL_R, color='g', linestyle='--', label='LCL')
plt.legend()
plt.title('R Chart')
plt.xlabel('Subgroup')
plt.ylabel('Subgroup Range')

plt.tight_layout()
plt.show()