Hi, 你好。我是茶桁。

咱们之前的课程就给大家讲了什么是人工智能，也说了每个人的定义都不太一样。关于人工智能的不同观点和方法，其实是一个很复杂的领域，我们无法用一个或者两个概念确定什么是人工智能，无法具体化。

我也是要给大家讲两个重要的概念，要成为一个良好的AI工作者，需要了解两个概念，一个是什么是优化问题，第二个呢就是什么是继续学习。

这一节开始，我们要开始进入机器学习的入门，这一部分只是机器学习的初级部分，我将其分成了三个部分，分别是：

1. 如何衡量向量的相似性（metric for tensor)
2. k-means算法进行聚类
3. 线性回归与梯度下降

但是整体课程的排程并不是严格按照这三个部分来排的，所以大家能看到，我本篇课程的标题也并不是「如何衡量向量的相似性（metric for tensor)」。以上三个部分仅仅是我们当前这一部分会讲到的内容，但是也是拆散了放入课程中的。

从一个案例开始

那这节课最初，让我们从一个实际案例来引入，开始我们的深度学习初级之旅。

那要给大家讲的第一个问题，我们叫做optimization, 也叫做优化问题。那这里，我们拿一个实际的项目来。

我们所在的城市，可能很多人会经常看到运钞车。这个运钞车其实也是银行花钱雇的，运钞车其实也不是银行的。

每次要使用运钞车的时候是需需要花钱，还比较贵。这样就会带来一个结果，专门有人来策划运钞车的运行路径。为什么要策划计划运钞车的运行路径呢？因为如果我们有一台ATM机，ATM机满了，那么面对的一个问题就是别人存不进去钱了，

另外很重要一点是，如果一个ATM机满了而且没有把钱取出来，那这个钱就相当于是浪费了。加入一个ATM机能存一百万，那晚拿出来一天、两天，对银行来说损失就比较大。

还有一种情况就是这个ATM机空了，那客户去取钱的时候也取不到钱，也就起不到ATM机的作用。而银行对ATM机所在地的房租也就相当于白费了。

试想一下，如果同时有两张卡，一张农行卡，一张工行的卡，在农行准备想取钱的时候取不出来，就到工行去取了。而每次农行都取不出来，那之后就用工行用的多了。

在这样的情况下, 一个城市有很多个点, 就需要有很多个运钞车。

比方说在城市中有很多个ATM机的站点，现在我们有k个运钞车。

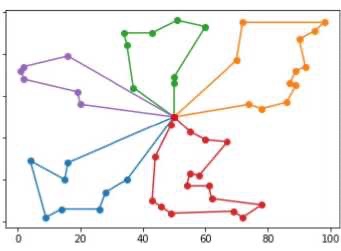
我们要策划一条线路，这个线路要使得所有的车，每个车每个点只走一遍，还要回到他出发的地方，而且这k个车运行的时间加起来是最小的。

那怎么样计划出这样一条路径呢？就这是一个非常典型的优化问题。对于此类的问题其实还有很多很相似的。

比如对于一家公司而言，手里的钱是有限的。如何把这些金额分配到不同的项目组中；

另外一个比方就是，对于一个公司来说如何选取合理的仓库的存货点，还有哪些仓库放哪些商品，能够让运输的车辆花的时间最少，能快速的去把这货物运输到不同的地方；这种物流问题是我最喜欢的问题之一。

或者我们制造一部手机，我们能花的钱就这么多，那怎么样能够在我们可以花的这个金额的范围内，如何选取最合理的元器件成本，让我们的手机达到最大的利润；

有很多约束条件，很多约束我们做决策的东西，总量不能大于多少。比方电的成本，水的成本等等，都要满足一定的关系才可以。这种东西我们就把它叫做约束条件。

要解决在约束条件下达成目标的这个问题，我们就把它叫做优化问题。

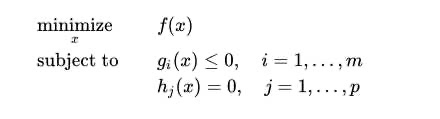
优化问题就是，我们可能会有不少的函数，这些函数去限定了之间的一种关系，也就是函数之间可能会有一些约束条件。比如图中的g_i(x)。

假设我们要造很多仓库，仓库加起来所花费的成本是什么样的, 花费的人力是什么样的。

最后要优化出来一个最小值就是我们的最小花费，或者所需要最少的时间。这种问题其实广泛存在于我们各个地方。

你点外卖每天在地图上做一个地图的规划，公司里做一笔投资，其实都是使用了类似这样的东西。

动态规划

我们要解决优化问题，其实有比较多的方法，今天来介绍最著名的一种，也是可以说是最重要的一种，动态规划的思想。

动态规划是一个什么样的情况？以这个问题引入一下。

想象一下有这么一个工厂，这个工厂是卖木头的，长度是一米的木头卖一块钱，长度2米的卖5块钱。

那么所以除非拿了一个一米的木头，否则不会有一个人像傻子一样说：把这个两米的木头截成两段。

图中我们可以看到，3米的就卖8块等等，到后面10米的卖30，11米的卖33。

那么现在你拿到了一个长度为8的一个木头，那你想想这个8米的木头是该直接卖，还是它切分掉去卖。切分掉去卖的话，如果用1和7，加起来就是18块钱，
2和6加起来就22块钱了，比8是不是就多了？

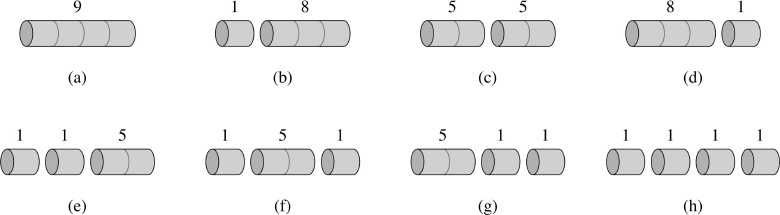
给你任意的一个长度n，然后我们要得出来这个n到底该怎么切分能够使得价格最大。怎么样能够让卖出去的价格最大。

思考一下咱们怎么解决这个问题。计算机有一个很很简单的方法，就是计算机有一个非常好的优点就是它可以做穷举。你可以让他去找什么，让他把所有东西全部都运行一遍就可以了。这是计算机的一个好处。

我们来思考一下咱们怎么样能够解决这个问题呢？

我们现在输入了一个长度是n的一个木头。它可以变成n和0，就是不切分。可以变成1和n-1, 变成2和n-2。一直截断到多少呢？可以变成n-n/2。

(0,n),(1, n-1),(2, n-2)…(n-n/2, n-n/2)

在这个情况下, 它分成1和n-1, n-1也面临了类似的问题。n-1是你直接返回n-1呢, 还是变成(1, n-2)，变成(2, n-3)。对于2，其实也有也会面临这样一个问题，是返回2呢，还是(2-1, 2-1)。如果我们要遍历的话，遍历的就应该是一个树。把这个树里面所有情况都找一遍，然后返回那个最大值就可以了。

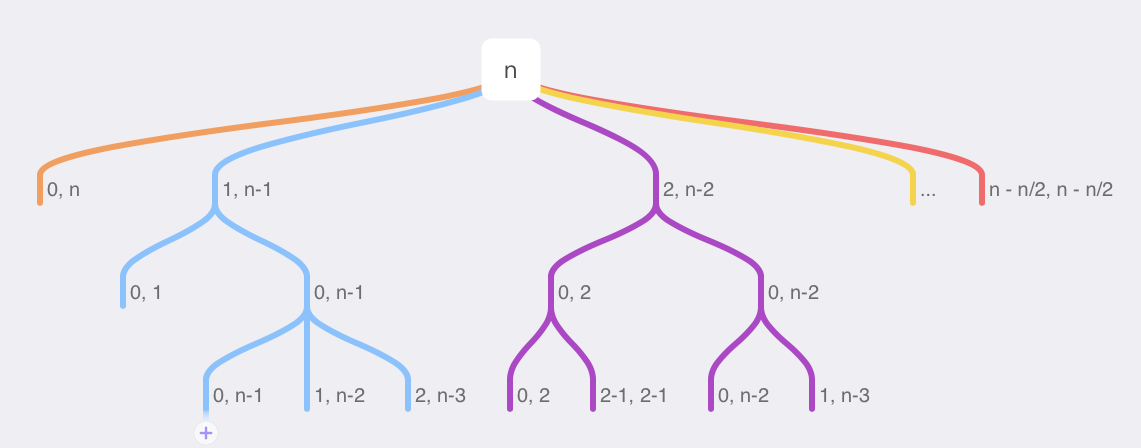
我们可以把所有的情况循环一遍，那我们现在来实现一下，你会发现其实一点也不难。

让我们来先定义一下所有的价格：

prices = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30 , 33]

我们要知道它的每一个商品直接的价钱，就是complete，我们来定义一个complete_price,

complete_price = { i+1: p for i, p in enumerate(prices)}
print(complete_price[9])

---
24

那如果这个时候是30，就会出问题。

print(complete_price[30])

---
KeyError: 30

遇到这种问题的时候不要非要去判断这个在不在里边,可以直接用detaultdict, 它是是一个带有默认值的Dictionary，如果这个值不存在的话，给它赋予一个默认值。

from collections import defaultdict

complete_price = defaultdict(int)

for i, p in enumerate(prices): complete_price[i+1] = p

print(complete_price[9])
print(complete_price[30])

这个时候如果是30, 它就有一个结果了。现在有了这样的一个基础数据，我们假如要写一个revenue,revenue就是营收，输入长度是n。

现在做一个很简单的方法：

def r(n):
    candidates = [complete_price[n]]

candidates等于价钱完全不切割是多少钱。然后我们写一个for循环：

for i in range(1, n):
    pass

接下来我们做个拆分，拆分左边就等于i, right就等于n-i:

left = i
right = n-i

这个时候整体的价格就等于complete_price[left], 再加完整的右边, complete_price[right]。

total_r = complete_price[left] + complete_price[right]

这里其实是有问题的, 如果我们在这里假设n现在是100, 假设运行到i是50, 那么complete_price[50] 其实是一个没有值的, 值是0。

就是数据里没有50的长度的价格，所以这个左边和右边其实是需要变成一个递归问题。

total_r = r(left) + r(right)
candidates.append(total_r)

现在写法写的稍微巧妙一些，这个就是我们刚才所说的遍历一遍，把所有的情况给拿出来,找到最大的返回出来。目前为止这个方法完整的代码如下：

def r(n):
    candidates = [complete_price[n]]

    for i in range(1, n):
        left = i
        right = n-i

        total_r = r(left) + r(right)
        candidates.append(total_r)
    return max(candidates)

这个时候我们来调用一下：

print(r(8))

---
22

这个22是怎么来的呢? 我们来看一下上面这段代码, 首先8进方法之后， 第2行告诉我们8完全不切割的话是多少，并赋值给candidates。

紧接着把它变成了1和7，2和6，3和5，4和4这样的问题。

假如到6的时候，又会去求一下这个6。右边是要变成6，那么6最大应该是多少。

这个代码其实可以写成更加Python化的方式，我先写一遍上面的，是希望能让大家知道这个代码是怎么来的，现在让我们来用Python的方式来解决：

# 优化为Python向
def r(n):
    return max([complete_price[n]] + [r(i) + r(n-i) for i in range(1, n)])

print(r(8))

---
22

也就是，以上方法里定义的内容，完全可以压缩成一句话解决。你们可以仔细的研究一下这两段的相同点和差别。

现在的问题就是我们缺了一个记录他中间分割步骤的内容，这个也简单，我们稍微改变一下代码，将return改为赋值，然后给他加一个分割方法：

candidates = [(complete_price[n], (n, 0))] + [(r(i) + r(n-i), (i, n-i)) for i in range(1, n)]

其中我们添加了(n, 0), 还有(i,n-i)。

然后我们还要给他加上最优值：

optimal_price, split = max(candidates)

如果这其中你要是看不出逻辑过程，那你需要一些更多的练习。好好的再去回去看看我之前写的AI秘籍中的Python基础教程篇。

对于熟练的Python的工程师来说，应该熟悉这种方式才对。第一次咱们实现的方法，其实是C和Java的一种方法。如果是Python的话，你需要熟悉Python，直接会写成这个样子。

我们定义了一个candidates, 后面将风格方式定义进去并赋值给它。

然后我们使用optimal_price来接收它的最优价格。

接着，我们添加一个solution变量，solution是n的时候就找到了它的分割过程。

# 在方法外定义一个solution
solution = {}

# 在方法内赋值solution[n]

def r(n):
    ...
    solution[n]  = split

最后，我们还是将最优价格给返回出去。

return optimal_price

来看一下solution[8]

print(solution[8])

---
(6, 2)

我们如果在这里debug一下这个solution，运行完之后solution如下：

是8的情况下变成6和2，现在就要看一下6的时候怎么切分？6的时候变成6和0。

好，现在我们来看一个更复杂的问题，我们将它变成33, 33你会发现他运行的时间很久。刚刚我们运行8，或者我们重新运行9的时候，速度都还可以，很快就能得到结果。但是运行33的时候就会非常的缓慢。知道这是为什么吗？

在这段代码中，现在有一个n，n接下来会拆分成了n-1个问题，其实是要进行n-1个循环。那每个n-1的循环里面又有两个调用了这个运算。所以在整个计算的次数的复杂性，对于一个n来说，它整个的运行时间应该是：2 * (n-1) * 2 * (n-2) * … = 2^n * n!，就等于2的n次方再乘上n的阶乘。

这样的话，结果就是它的运行时间会非常非常的久。那我们就需要对代码进行优化了。

如果现在仔细分析一下的话，会发现之所以运行的慢，问题在于很多重复的值其实被重复运算了。同样是n-3这个事，不仅在n-1向下分支中会计算一次，在其他的分支也会再计算很多次。有很多的值是被重复运算了。

为了解决重复运算的问题，我们可以做一个非常简单的方法。既然很多计算是重复的，那我定义一个变量去记录这些曾经计算过的，再遇到的时候就不要去计算不就完了：

cache = {}

def r(n):
    if n in cache: return cache[n]
    ...
    cache[n]  = optimal_price

    return optimal_price

print(r(33))

---
99

如果n在cache里面, 直接return cache[n], 如果它不在里边的话就往下继续运行，每次求完解的之后，我们让cache[n]等于optimal_price。这样就简单多了。

我们最后求了一下33，瞬间就得到了99的答案。

这个cache其实是很简单的一个东西，但是它其实是很重要的一种思想。在一九二几年、三几年的时候，当时有一个数学家叫Richard Bellman。Bellman发现在整个数学计算中有相当的一类问题，都牵扯到了一个相似的问题：over-lapping sub-problem，就是子问题的重复。

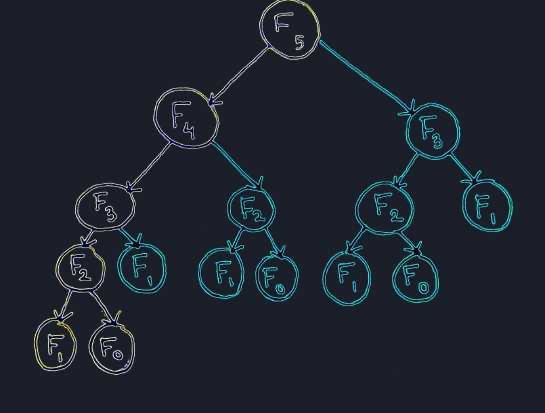
Bellman就提出来了一种方法，他就说我们解决这种问题其实有一个很简单的方法，用一张表格，不断地记录不断地查表，就是不断地写表查表。

就把值和结果都一一对应的写入表中，我们发现问题的时候，在这个表里面重新查一遍，看一下有没有这个值，存不存在。

当时Bellman把这种方法叫做Dynamic，不断地、持续地、变化的、动态的。programming在我们现在意思是编程，在一九二几、一九三几年的时候，是指把东西写到表格里以及从表格里面拿出来。

那为什么后来演化成编程的意思，因为早些时候，冯诺伊曼当年制作的那个机器写的是纸带，就是给你一个一个的纸带，这个纸带每一行会打八个洞，就是当时冯诺伊曼最早的计算机。这8个洞里边有一些是透光的，有一些是不透光的，其实就是一条一条计算机命令。

这其实也是一个写表读表的过程，后来programming就有了编程的意思。但是Bellman当年提出来的这个意思，Dandep programming就是不断地写表和查表。它针对的是所有一切有这个over-lapping sub-problem的问题，都可以用这种简单的方法，可以大幅度的减少计算性。

在很多地方学动态规划的时候，很多书上教动态规划的时候往往是直接给一个解法。不知道您有没有看过那些算法的书，在动态规划里往往会有一个表，这个表格很重要。

如果不用动态规划的话，这个问题也是能解决的。世界上几乎所有的这种优化问题不用动态规划都是可以解决的。但是理论上是要给你一个运算能力无限强，存储空间无限大的计算设备。

显然不太可能，所以我们就需要这样写到一个表格里边，记一个记录表格。这个就是我们动态规划的核心思想。

关于「动态规划的详解」之后有机会我去专门写个算法的相关课程，在这里就把动态规划的核心思想给大家介绍了。

我们现在来继续看代码，刚才我们算了一下33这个值，得到了99。但现在我们知道了能卖多少钱，但是我们还不知道到底怎么个拆分法。

要拆分的话我们就要把这个solution给它parse一下，再继续定义一个方法：

def parse_solution(n, cut_solution):
    left, right = cut_solution[n]

    if left == 0 or right == 0: return [left+right, ]

    else:
        return parse_solution(left, cut_solution) + parse_solution(right, cut_solution)

print(r(18))
print(parse_solution(18, solution))

---
52
[10, 6, 2]

我们看一下left和right，将分割分别传进来，那如果left和right是0的话，比如10， 写成(10, 0)， 其实意思就是10就不用切分了，直接返回left和right就可以了。

那如果说它里边不是0，假如说是37，切分17和20，我们就要知道17该怎么分，20该怎么分。所以就返回:

return parse_solution(left, cut_solution) + parse_solution(right, cut_solution)

最后我们看到了18的切分结果，就被切分成[10, 6, 2]。

具体的切割过程也可以获得。

在Python里边呢这个是一个非常非常经典的动态规划问题。经过一个比较简单的方法，把重复问题给解决了。

再跟大家普及一个知识，在Python里面有一个好处就是它把很多常见的功能其实都已经想到，做了切分了。

比方说Python自带的库里面就有一个functools, 它有一个lru_cache，就是least recent used, 最近最少使用。

我们如果在直接写一个cache，它会存在一个问题。当n特别大的时候，那么cache的size也会变得特别的大。这个时候我们就需要一种机制，来让cache保留最需要保留的东西，保留那些最重要的东西，不要把所有的信息全部弄进去。

这个lru_cache帮我们实现了这个功能,它会把最近最少使用过的这些值删去, cache的这个size会保持在一个比较固定的范围内。

这个函数是一个装饰器，小伙伴们是否还记得我在Python课程中介绍过装饰器以及其使用？

我们来使用一下这个装饰器:

@lru_cache(maxsize=2**10)

这里定义了一下maxsize等于2的10次方，就是最多可以存2的10次方个值。

那这里和我们方法里的这一段内容其实是一摸一样：

if n in cache: return cache[n]
...
cache[n] = optimal_price

当我们调用这个函数的时候, 如果函数的参数曾经被计算过，那么就直接返回这个值。如果没有被计算过，就计算一遍，再把这个值写下来。

那我们使用了这个装饰器之后，我们对cache的使用的这两句代码就可以删掉了。

lru_cache的作用都懂了吧？以后遇到一个程序很慢的时候，就可以用它来做优化。

那其实今天这节课程把这个函数看懂，几乎所有的动态规划的问题的主体思路就都懂了。因为所有的动态规划的问题都包含了以下几个问题：

1. 识别子问题 sub-problems dividing
2. 识别子问题中的重叠特点 over-lapping sub-problem
3. 存储子问题的答案 cache sub-solutions
4. 合并问题答案 combine solutions
5. 解析答案 parse solutions

这是所有的动态规划的特点，当你发现一个问题可以被分解成子问题，而且子问题有重复的时候，就可以用这种方法去优化它。

以后大家面试，大概率会遇到这种问题。只要按照这个方法来思考的话问题基本上就不大了。

但是动态规划其实也是有一个极限，曾经有一段时间人们以为动态规划可以解决很多问题，几乎可以解决所有常见的问题。但是后来人们发现，当限制条件特别多，或者问题已经复杂到非常难的去识别此问题了。可能它是包含了子问题的关系，但是因为这个问题太复杂了，所以我们没办法去把它分割出来，我们没有办法去识别它。

动态规划是一种思维方法，一种思维类型。比方计算机里面的图论问题，并不是只能把它变成图论问题，不用图论完全可以解决，但是不太好弄。

所以，动态规划其实也有它的局限性，人们为了解决更多问题就提出了更多的方法，其中一种方法就叫做机器学习。

好，我们下节课，就好好的来讲讲机器学习。本节课的最后，我将之前咱们写的那段代码完整版贴在这里：

from collections import defaultdict
from functools import lru_cache

prices = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30 , 33]
complete_price = defaultdict(int)

for i, p in enumerate(prices): complete_price[i+1] = p

solution = {}
cache = {}

@lru_cache(maxsize=2**10)
def r(n):

    candidates = [(complete_price[n], (n, 0))] + [(r(i) + r(n-i), (i, n-i)) for i in range(1, n)]
    optimal_price, split = max(candidates)

    solution[n] = split
    return optimal_price

def parse_solution(n, cut_solution):
    left, right = cut_solution[n]

    if left == 0 or right == 0: return [left+right, ]

    else:
        return parse_solution(left, cut_solution) + parse_solution(right, cut_solution)

print(r(18))
print(parse_solution(18, solution))