目录链接:
力扣编程题-解法汇总_分享+记录-CSDN博客
GitHub同步刷题项目:
https://github.com/September26/java-algorithms
原题链接:力扣
描述:
给你一个以 (radius, xCenter, yCenter) 表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2) ,其中 (x1, y1) 是矩形左下角的坐标,而 (x2, y2) 是右上角的坐标。
如果圆和矩形有重叠的部分,请你返回 true ,否则返回 false 。
换句话说,请你检测是否 存在 点 (xi, yi) ,它既在圆上也在矩形上(两者都包括点落在边界上的情况)。
示例 1 :
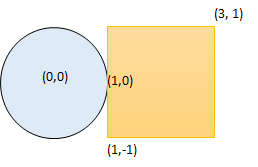
输入:radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1 输出:true 解释:圆和矩形存在公共点 (1,0) 。
示例 2 :
输入:radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1 输出:false
示例 3 :
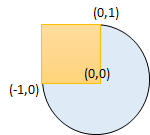
输入:radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1 输出:true
提示:
1 <= radius <= 2000-104 <= xCenter, yCenter <= 104-104 <= x1 < x2 <= 104-104 <= y1 < y2 <= 104
解题思路:
/**
* 1401. 圆和矩形是否有重叠
* 解题思路:
* 首先,如果圆心在矩形内,则直接返回true即可。
* 其它情况,我们就要找圆心距离矩形的最近距离了。
* 如果x轴在x1到x2的范围内,则最近的距离就是min(abs(yCenter - y1), abs(yCenter - y2))。同理,min(abs(xCenter - x1), abs(xCenter - x2))也符合,取两者较小值。
* 如果都不符合,则最小值就是距离4个顶点的最近值。
* 为了方便运算,所以我们求平方之后的值进行计算。distance <= pow(radius, 2)就是在范围内。
*/
代码:
class Solution1401
{
public:
int getDistance(int xCenter, int yCenter, int x, int y)
{
return pow(xCenter - x, 2) + pow(yCenter - y, 2);
}
bool checkOverlap(int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2)
{
if (((xCenter >= x1 && xCenter <= x2) || (xCenter >= x2 && xCenter <= x1)) && ((yCenter >= y1 && yCenter <= y2) || (yCenter >= y2 && yCenter <= y1)))
{
return true;
}
int distance = 20000;
if ((xCenter >= x1 && xCenter <= x2) || (xCenter >= x2 && xCenter <= x1))
{
distance = min(abs(yCenter - y1), abs(yCenter - y2));
}
if ((yCenter >= y1 && yCenter <= y2) || (yCenter >= y2 && yCenter <= y1))
{
distance = min(distance, min(abs(xCenter - x1), abs(xCenter - x2)));
}
distance = pow(distance, 2);
distance = min(distance, getDistance(xCenter, yCenter, x1, y1));
distance = min(distance, getDistance(xCenter, yCenter, x1, y2));
distance = min(distance, getDistance(xCenter, yCenter, x2, y1));
distance = min(distance, getDistance(xCenter, yCenter, x2, y2));
return distance <= pow(radius, 2);
}
};