一、说明

DBSCAN 代表基于密度的带噪声应用程序空间聚类。它是一种流行的聚类算法，用于机器学习和数据挖掘，根据数据集中紧密排列在一起的点与其他点的距离对点进行分组。

二、DBSCAN的算法原理

DBSCAN 的工作原理是将数据划分为由密度较低的区域分隔的点的密集区域。它将聚类定义为数据集中有许多点彼此靠近的区域，而远离任何聚类的点被视为异常值或噪声。

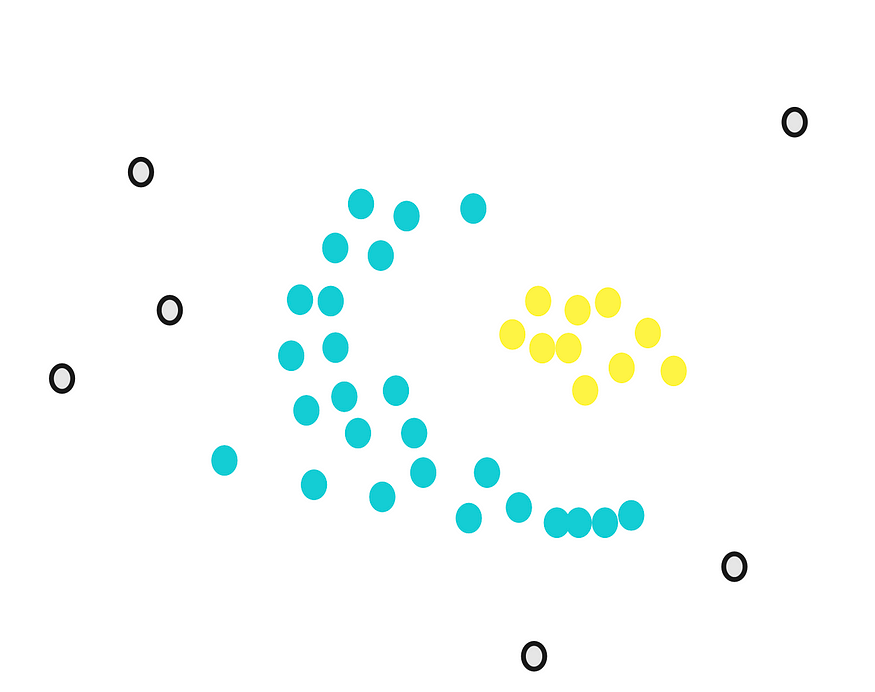
为了理解算法的工作原理，我们将通过一个简单的示例。假设我们有一个如下所示的点数据集：

我们的目标是将这些点聚集成密集的组。首先，我们计算接近每个点的点数。例如，如果我们从绿点开始，我们在它周围画一个圆。

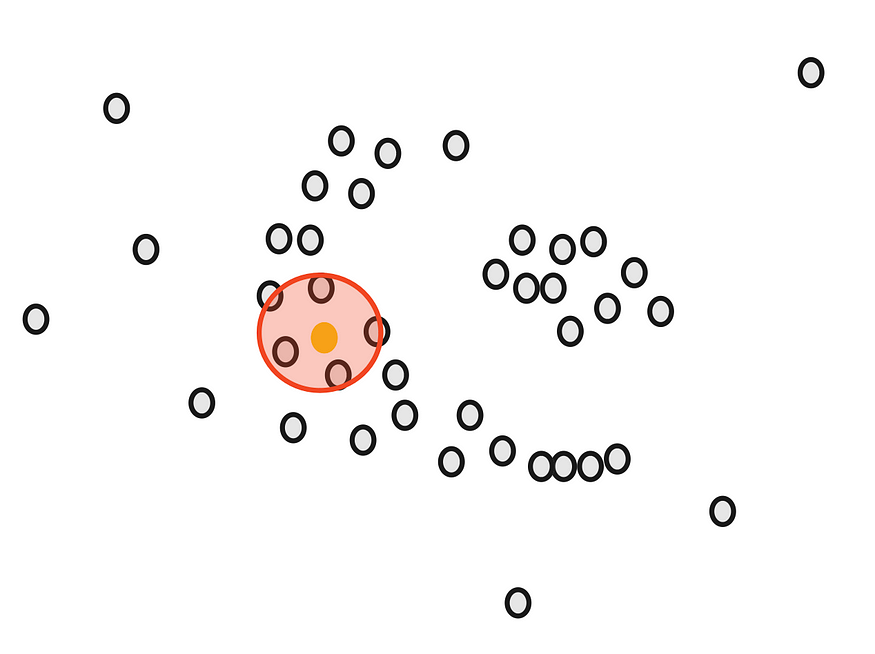
图片由作者提供。

圆的半径ε（epsilon）是我们在使用DBSCAN时必须确定的第一个参数。

画完圆后，我们计算重叠。例如，对于我们的黄点，有 5 个接近点。

同样，我们计算所有剩余点的关闭点数。

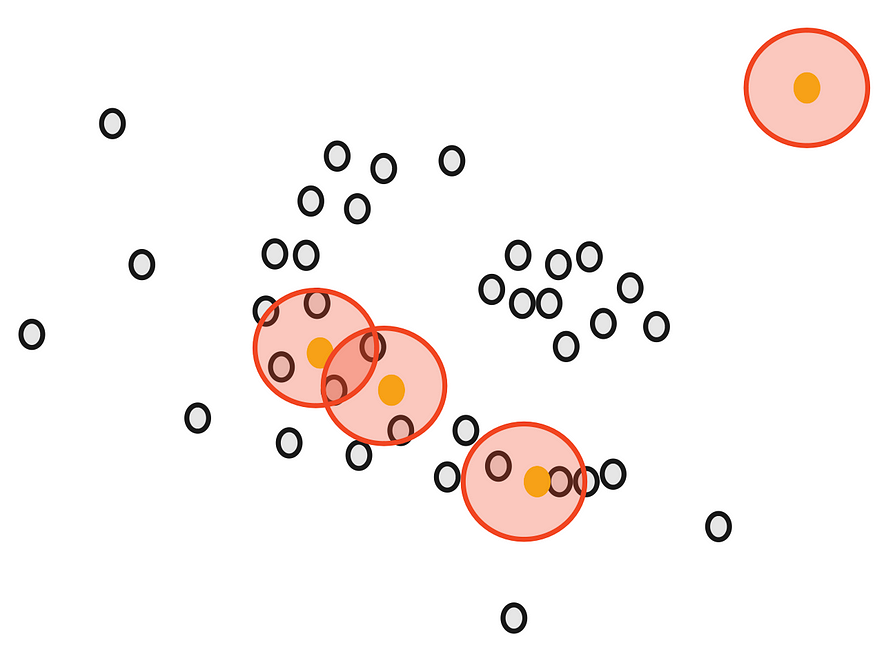
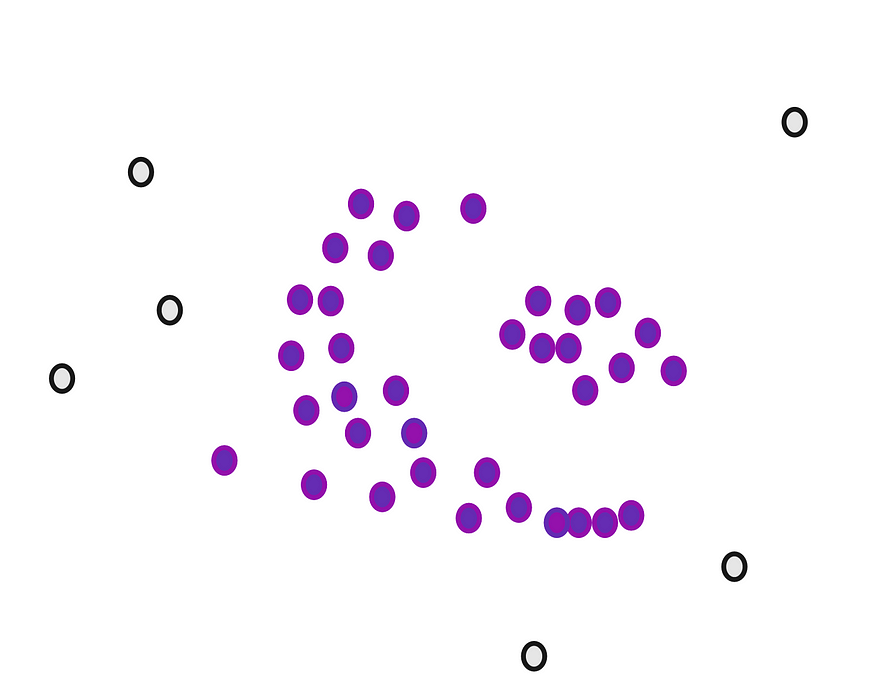
接下来，我们将确定另一个参数，最小点数 m。如果每个点至少接近 m 个其他点，则将其视为核心点。例如，如果我们以 m 为 3，那么紫色点被视为核心点，但黄色点不是，因为它周围没有任何接近点。

然后，我们随机选择一个核心点并将其分配为第一个聚类中的第一个点。接近该点的其他点也分配给同一聚类（即，在所选点的圆内）。

然后，我们将其扩展到其他接近的点。

当我们无法为第一个集群分配更多核心点时，我们会停止。一些核心要点即使接近第一组，也无法指定。我们画出这些点的圆圈，看看第一个聚类是否靠近核心点。如果有重叠，我们把它们放在第一个集群中。

但是，我们不能分配任何非核心点。它们被视为异常值。

现在，我们仍然有核心点没有分配。我们从中随机选择另一个点并重新开始。

DBSCAN 按顺序工作，因此请务必注意，非核心点将分配给满足接近度要求的第一个集群。

三、python实现

我们可以从中使用类。在实现任何模型之前，让我们更好地了解该类。我们可以将一些参数传递给对象。DBSCANsklearnDBSCAN

eps：将它们视为相邻点的两个点之间的最大距离。彼此相距不远的点被视为同一聚类的一部分。eps
min_samples：将一个点视为核心点所需的最小点数。小于相邻点的点被标记为噪点。min_samples
metric：用于测量点之间距离的距离度量。默认情况下，使用欧氏距离，但可以使用其他指标，例如曼哈顿距离或余弦距离。
algorithm：用于计算每个点的最近邻的算法。默认值为，它根据数据的大小和维度选择最合适的算法。其他选项包括、和。"auto""ball_tree""kd_tree""brute"
leaf_size：或算法中使用的叶节点的大小。较小的叶子尺寸导致更准确但更慢的树木构造。ball_treekd_tree
p：闵可夫斯基距离度量的功率参数。当，这相当于曼哈顿距离，当，这相当于欧几里得距离。p=1p=2
n_jobs：用于并行计算的 CPU 内核数。设置为使用所有可用内核。-1

现在，让我们先生成一些虚拟数据。

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# generation of nested dummy data
X, y = make_blobs(n_samples=1000, centers=[[0, 0], [0, 5], [5, 5]], cluster_std=[1.0, 0.5, 1.0])

plt.scatter(X[:,0], X[:,1], color='blue')
plt.show()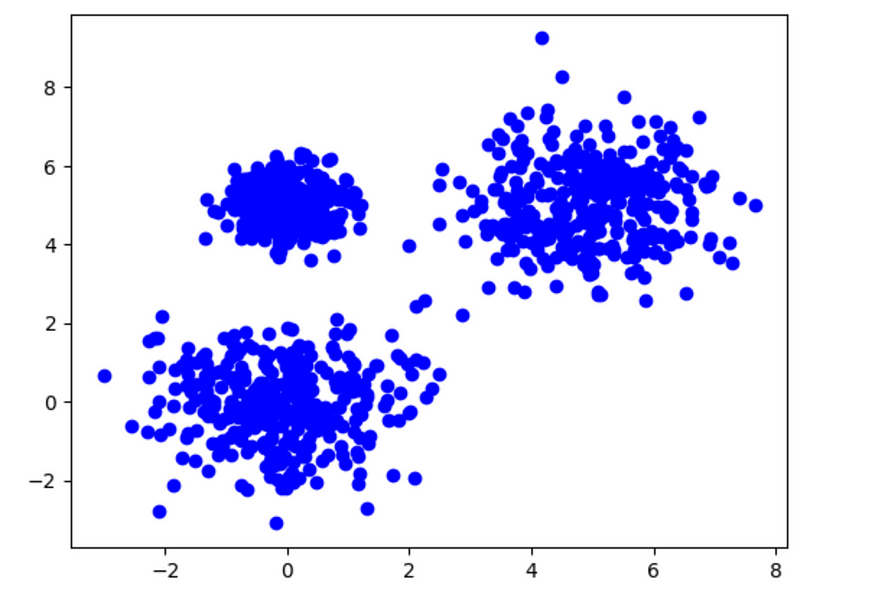

数据。图片由作者提供。

并且，模型：

from sklearn.cluster import DBSCAN

# model
dbscan = DBSCAN(eps=0.5, min_samples=5)
labels = dbscan.fit_predict(X)

# the number of clusters found by DBSCAN
n_clusters = len(set(labels)) - (1 if -1 in labels else 0)
print(f"Number of clusters found by DBSCAN: {n_clusters}")
# Number of clusters found by DBSCAN: 3

现在，让我们绘制聚类。

import numpy as np

unique_labels = set(labels)
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):
    if k == -1:
        col = [0, 0, 0, 1]  # Black color for noise points (label=-1)
    class_member_mask = (labels == k)
    xy = X[class_member_mask]
    plt.scatter(xy[:, 0], xy[:, 1], s=50, c=[col], marker='o', alpha=0.5)

plt.title('DBSCAN Clustering')
plt.show()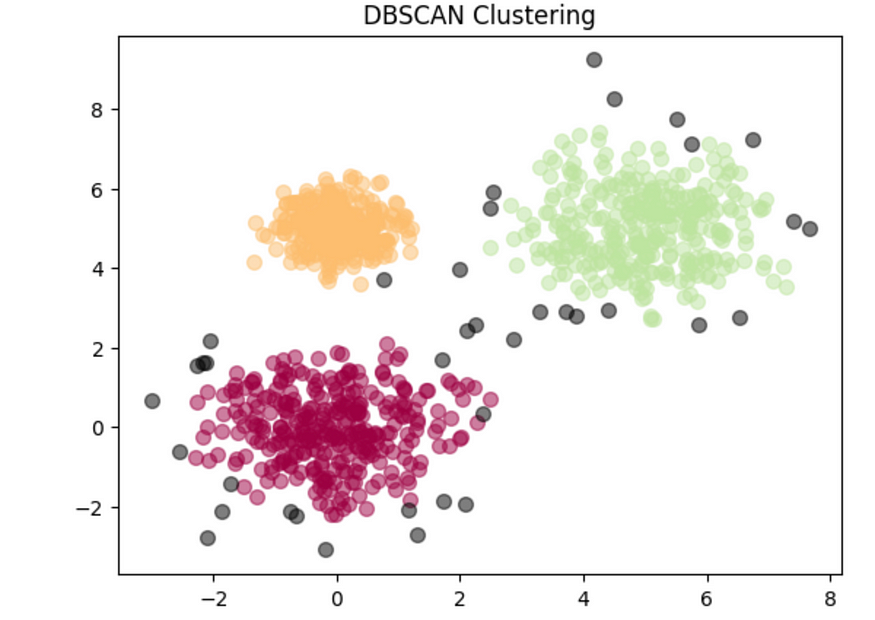

DBSCAN 集群。图片由作者提供。

# attributes of the dbscan object
print("Indices of core samples: ", dbscan.core_sample_indices_)
print("Copy of each core sample found by training: ", dbscan.components_)
print("Labels: ", dbscan.labels_)
print("Number of features seen during fit: ", dbscan.n_features_in_)