机器学习——K最近邻算法(KNN)
文章目录
- 前言
- 一、原理
- 二、距离度量方法
- 2.1. 欧氏距离
- 2.2. 曼哈顿距离
- 2.3. 闵可夫斯基距离
- 2.4. 余弦相似度
- 2.5. 切比雪夫距离
- 2.6. 马哈拉诺比斯距离
- 2.7. 汉明距离
- 三、在MD编辑器中输入数学公式(额外)
- 四、代码实现
- 2.1. 用KNN算法进行分类
- 2.2. 用KNN算法进行回归
- 五、模型的保存和加载
- 总结
前言
在传统机器学习中,KNN算法是一种基于实例的学习算法,能解决分类和回归问题,而本文将介绍一下KNN即K最近邻算法。
一、原理
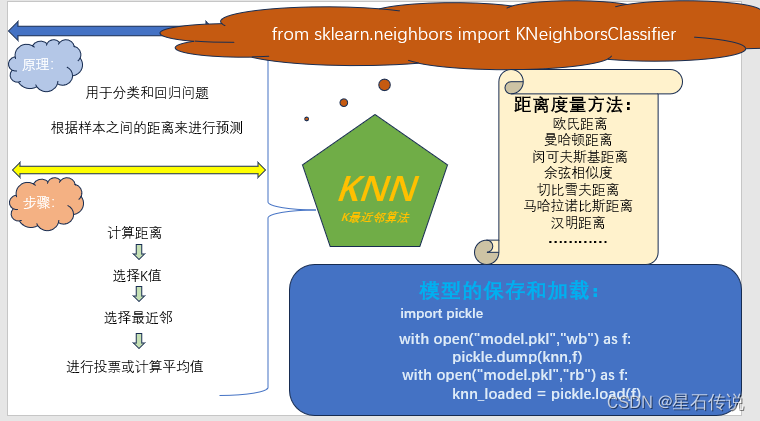
K最近邻(KNN)算法是一种基于实例的学习算法,用于分类和回归问题。它的原理是根据样本之间的距离来进行预测。
核心思想是通过找到与待分类样本最相似的K个训练样本,来确定待分类样本的类别或者预测其数值。
假设存在一个样本数据集(训练集),并且样本集中每个数据都存在标签(即知道样本集中数据的分类情况)
KNN算法的步骤如下:
-
计算距离:对于给定的未知样本(没有标签值的测试集),计算它与训练集中每个样本的距离。常用的距离度量方法有欧氏距离、曼哈顿距离等。
-
选择K值:选择一个合适的K值,即要考虑的最近邻的数量。
-
选择最近邻:从训练集中选择K个距离最近的样本。
-
进行投票或计算平均值:对于分类问题,根据最近邻的标签进行投票,选取票数最多的标签作为预测结果。对于回归问题,根据最近邻的值计算平均值作为预测结果。
按我的理解其实就是将待分类的样本与训练集中的每个样本去计算距离,然后从训练集中选择K个与待分类样本最靠近的几个样本,然后再根据选取得最靠近的几个样本得标签值进行投票来分类。
对于回归问题,则统计K个最近邻样本的数值,然后通过平均或加权平均的方式计算出待分类样本的数值。
如图所示(可看出K值的选择对结果有很大的影响):
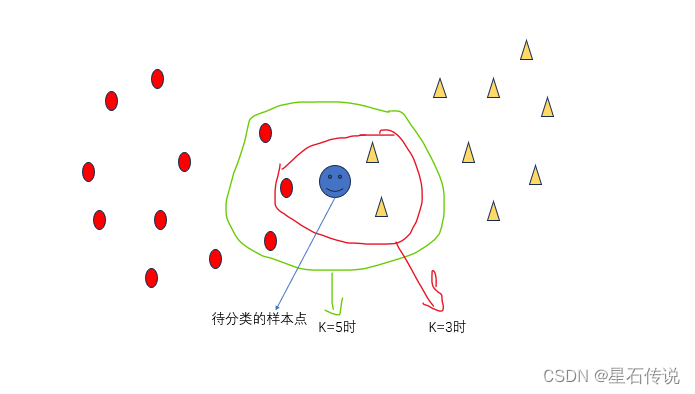
当K=3时,根据距离计算,待分类的样本点被划为黄色那一类;(因为2>1)
当K=5时, 根据距离计算,待分类的样本点被划为红色那一类;(因为3>2)
二、距离度量方法
参考文献
https://zhuanlan.zhihu.com/p/354289511
以下是一些常见的距离度量方法:
2.1. 欧氏距离
欧氏距离(Euclidean Distance):欧氏距离是最常见的距离度量方法,它是两个向量之间的直线距离。对于两个n维向量x和y,欧氏距离的计算公式为:
d ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 d(x,y) = \sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}} d(x,y)=i=1∑n(xi−yi)2
其中,xi和yi分别表示向量x和y的第i个元素。
例如当n = 2 时,这就是中学学的二维平面中两点之间距离公式的计算了。
2.2. 曼哈顿距离
曼哈顿距离(Manhattan Distance):曼哈顿距离是两个向量之间的城市街区距离,也称为L1距离。对于两个n维向量x和y,曼哈顿距离的计算公式为:
d
(
x
,
y
)
=
∑
i
=
1
n
∣
x
i
−
y
i
∣
d(x,y) = \sum_{i=1}^{n} |x_{i} -y_{i}|
d(x,y)=i=1∑n∣xi−yi∣
2.3. 闵可夫斯基距离
闵可夫斯基距离(Minkowski Distance):闵可夫斯基距离是欧氏距离和曼哈顿距离的一般化形式,它可以根据参数p的不同取值变化为不同的距离度量方法。对于两个n维向量x和y,闵可夫斯基距离的计算公式为:
d
(
x
,
y
)
=
∑
i
=
1
n
∣
x
i
−
y
i
∣
p
p
d(x,y) = \sqrt[p]{\sum_{i=1}^{n}|x_{i}-y_{i}|^{p}}
d(x,y)=pi=1∑n∣xi−yi∣p
其中,xi和yi分别表示向量x和y的第i个元素,p为参数,当p=2时,闵可夫斯基距离等价于欧氏距离;当p=1时,闵可夫斯基距离等价于曼哈顿距离。
2.4. 余弦相似度
余弦相似度(Cosine Similarity):余弦相似度是衡量两个向量方向相似程度的度量方法,它计算两个向量之间的夹角余弦值。对于两个n维向量x和y,余弦相似度的计算公式为:
c o s ( θ ) = ∑ i = 1 n ( x i ∗ y i ) ∑ i = 1 n ( x i ) 2 ∗ ∑ i = 1 n ( y i ) 2 cos(\theta ) = \frac{\sum_{i=1}^{n}(x_{i} * y_{i})}{\sqrt{\sum_{i=1}^{n}(x_{i})^{2}}*\sqrt{\sum_{i=1}^{n}(y_{i})^{2}}} cos(θ)=∑i=1n(xi)2∗∑i=1n(yi)2∑i=1n(xi∗yi)
2.5. 切比雪夫距离
切比雪夫距离(Chebyshev Distance):切比雪夫距离是两个向量之间的最大绝对差距。对于两个n维向量x和y,切比雪夫距离的计算公式为:
d
(
x
,
y
)
=
m
a
x
i
(
∣
p
i
−
q
i
∣
)
d(x,y) = \underset{i}{max}(|p_{i} -q_{i}|)
d(x,y)=imax(∣pi−qi∣)
2.6. 马哈拉诺比斯距离
马哈拉诺比斯距离(Mahalanobis Distance):马哈拉诺比斯距离是一种考虑特征之间相关性的距离度量方法。它首先通过计算协方差矩阵来衡量特征之间的相关性,然后计算两个向量在经过协方差矩阵变换后的空间中的欧氏距离。对于两个n维向量x和y,马哈拉诺比斯距离的计算公式为:
d = ( x ⃗ − y ⃗ ) T S − 1 ( x ⃗ − y ⃗ ) d = \sqrt{(\vec{x}-\vec{y})^{T}S^{-1}(\vec{x}-\vec{y})} d=(x−y)TS−1(x−y)
其中,x和y分别表示向量x和y,S为x和y的协方差矩阵。
2.7. 汉明距离
汉明距离(Hamming Distance):汉明距离是用于比较两个等长字符串之间的差异的度量方法。对于两个等长字符串x和y,汉明距离的计算公式为:
d
=
1
N
∑
i
=
1
n
1
x
i
≠
y
i
d = \frac{1}{N}\sum_{i=1}^{n}1_{x_{i}\neq y_{i}}
d=N1i=1∑n1xi=yi
三、在MD编辑器中输入数学公式(额外)
在使用markdown文本编辑器时,对于数学公式的书写一般是使用到LaTeX这个排版系统,基于latex语法构建数学公式。
这对我这种刚开始接触的初学者是不友好的(在这之前还要学习LateX语法…)。
$$
$$
在这之间填入数学公式对应的LaTeX语法,就能获得对应的数学公式
对应的LaTeX语法可以从另一个编辑器——富文本编辑器 中获得:
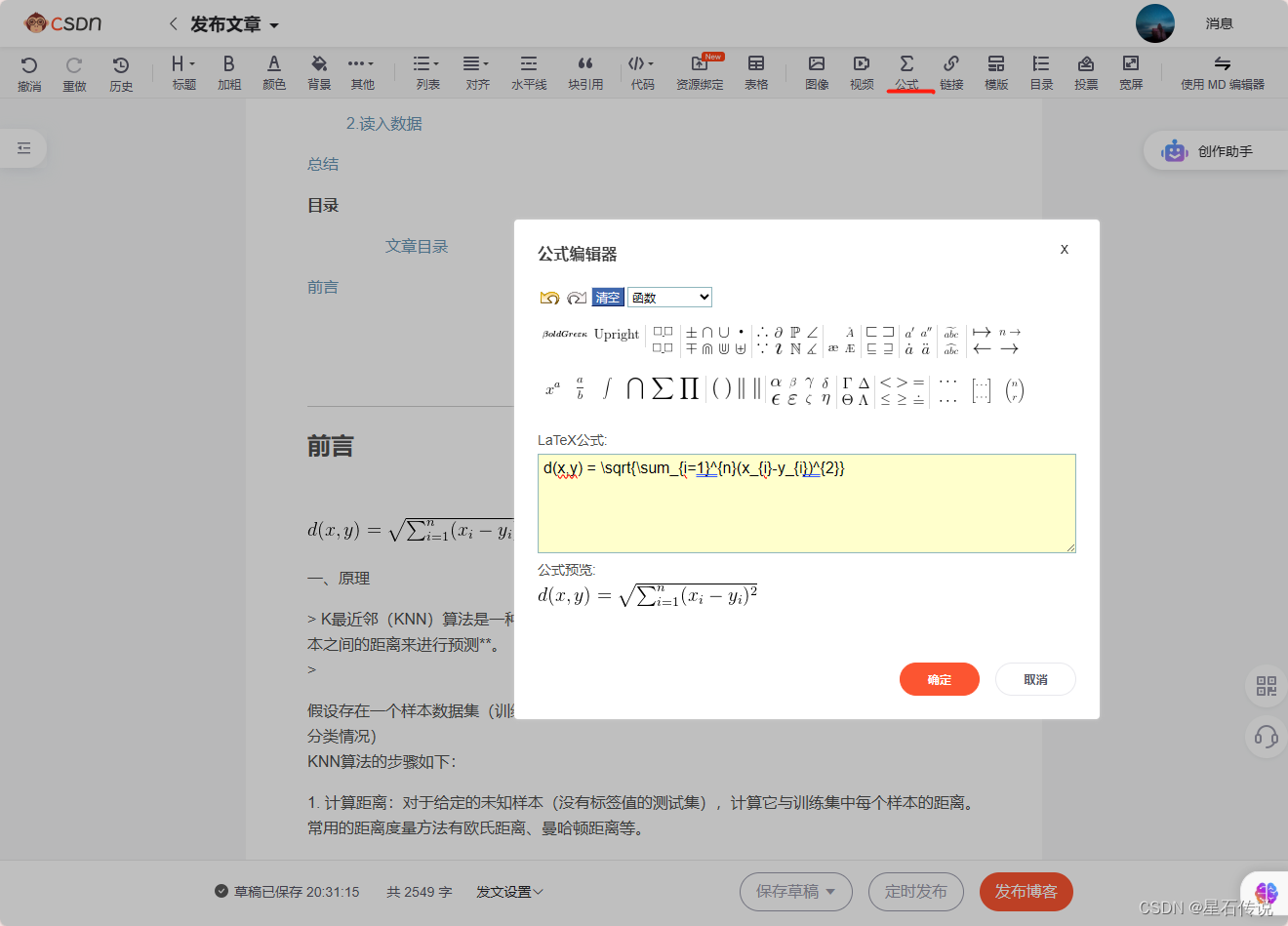
将LaTeX公式复制过来,d(x,y) = \sqrt{\sum_{i=1}{n}(x_{i}-y_{i}){2}}
$$
$$
放于这两个之间,可以得到对应公式:
d ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 d(x,y) = \sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}} d(x,y)=i=1∑n(xi−yi)2
嗯…,其实我也不太清楚为何我的Mardown编辑器中没有像富文本编辑器中那样的公式编辑器,(或许是要下载插件吗?),不用管这么多,能用就行。
四、代码实现
2.1. 用KNN算法进行分类
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42)
# 创建KNN分类器
knn = KNeighborsClassifier(n_neighbors=3)
#metric= "minkowski",距离度量默认是闵可夫斯基距离
# 拟合模型
knn.fit(X_train, y_train)
# 预测
y_pred = knn.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
Accuracy: 0.9833333333333333
2.2. 用KNN算法进行回归
from sklearn.neighbors import KNeighborsRegressor
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建KNN回归器
knn = KNeighborsRegressor(n_neighbors=3)
# 拟合模型
knn.fit(X_train, y_train)
# 预测
y_pred = knn.predict(X_test)
# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print("MSE:", mse)
MSE: 21.65955337690632
#计算R方值
print(knn.score(X_test,y_test))
0.7046442656646525
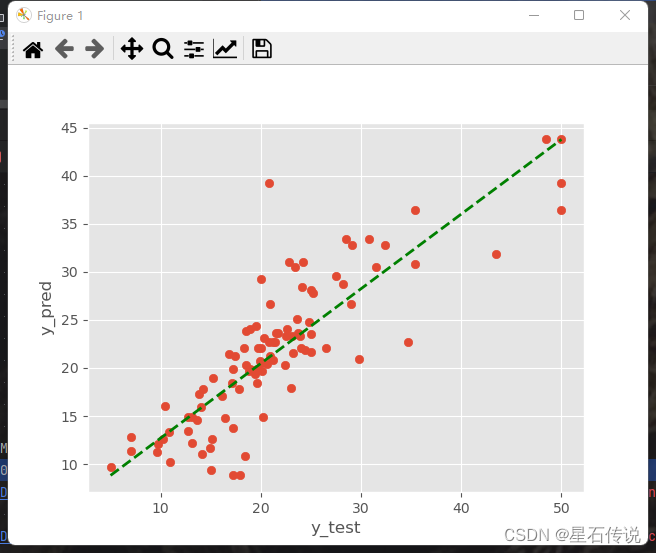
#绘图展示
import matplotlib.pyplot as plt
plt.style.use("ggplot")
plt.scatter(y_test,y_pred)
plt.plot([min(y_test),max(y_test)],[min(y_pred),max(y_pred)],"k--",color = "green", lw = 2,)
plt.xlabel("y_test")
plt.ylabel("y_pred")
plt.show()
均方误差:
M S E = ∑ i = 1 n ( y t − y p ) 2 n MSE = \frac{\sum_{i=1}^{n}(y_t - y_p)^{2}}{n} MSE=n∑i=1n(yt−yp)2
再用线性回归试一下:
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
coefficients = model.coef_
intercept = model.intercept_
# 构建回归公式
equation = f"y = {intercept} + {coefficients[0]}*x1 + {coefficients[1]}*x2 + ..."
# 计算R^2值
r2_score = model.score(X_test, y_test)
print("R^2值:", r2_score)
R^2值: 0.6687594935356289
这些模型都是十分简单的模型,还未经过参数的调优和算法的优化。
五、模型的保存和加载
#模型的保存和加载
import pickle
with open("model.pkl","wb") as f:
pickle.dump(knn,f)
with open("model.pkl","rb") as f:
knn_loaded = pickle.load(f)
print(knn_loaded.score(X_test,y_test))
0.7046442656646525
总结
本文从KNN算法的原理:(根据样本之间的距离来预测)出发,介绍了一些常见的距离度量方法,另外也介绍了一下在Markdown编辑器中输入数学公式,最后就是KNN算法在python中的分类和回归代码的实现。最后的最后就是模型的保存和加载。
道可道,非常道;名可名,非常名。
–2023-9-10 筑基篇