前言

之前看 PRML 时碰到了 变分相关的问题，所以找了一本书特地来学习一下

1 第一章 变分法基础

1.1 泛函 与 一些简单的变分问题

该节引出泛函的定义 ，介绍一个基本的泛函问题 并且 沿用经典的微积分有限元分析，对泛函做出类似的分析

变化量（variable quantities）被称为 泛函,指的是 自变量本身是一个函数的函数

例如 $J[y]={\int }_a^b{y}^{\prime 2}(x)dx$ 定义了一个泛函

一个更加一般的情形是
$$J[y]={\int }_a^{b}F\left[x,y(x),y^{\prime }(x)\right]dx$$

涉及泛函概念的问题的特定实例在三百多年前就被考虑过了，事实上，这一领域的第一个重要结果要归功于欧拉(1707 - 1783)。然而，迄今为止，"函数微积分 "仍不具备可与经典分析方法（即普通的 “函数微积分”）相媲美的通用方法。

要理解变分问题和方法的基本含义 要理解变分微积分的问题和方法的基本含义，很重要的一点是要了解它们与经典微分析的关系，即与 n个变量函数的关系。 因此，考虑一个形式为
$$J[y]={\int }_a^{b}F\left(x,y,y^{\prime }\right)dx,y(a)=A,y(b)=B$$
的泛函。

沿用经典微积分理论，我们可以切分 $[a,b]$ 区间 进行求和
$$a=x_0,x_1,\dots ,x_n,x_{n+1}=b,$$
$$J\left(y_1,\dots ,y_n\right)=\sum _{i=1}^{n+1}F\left(x_i,y_i,\frac{y_i-y_{i-1}}{h}\right)h$$
where
$$y_i=y\left(x_i\right),h=x_i-x_{i-1}.$$

利用这种方式解决 泛函问题被称为 有限差分法（finite differences。通过用多边形线代替 通过用多边形线代替平滑曲线，他将寻找函数极值的问题简化为寻找 n 个变量的函数极值的问题。

1.2 Function Spaces/ 赋范线性空间

本章讨论了 函数空间、重要的赋范线性空间（使得我们可以定义函数之间的距离），以及定义泛函的连续性（根据函数空间中函数之间的距离）

当我们去讨论 n 个变量（函数）的问题时，我们会很自然的去使用代数的语言：将$\left(y_1,\dots ,y_n\right)$当成时 n 维空间中的点。

函数空间：空间中的元素是函数时，即为 函数空间。

事实上，我们的函数空间很多时候取决于我们讨论的问题，例如当我们讨论这样的问题时：
${\int }_a^{b}F\left(x,y,y^{\prime }\right)dx$我们希望我们的函数是一维可导的连续函数，而这样的问题时即为二维可导的连续函数${\int }_a^{b}F\left(x,y,y^{\prime },y^{\prime \prime }\right)dx$

在赋范线性空间中我们可以定义 $x$ and $y$ 的距离为 $\Vert x-y\Vert$的值.

在接下来的讨论中，下面这些 赋范线性空间是很重要的：

1. $\mathcal{C}(a,b)$ : 即所有 [a,b] 间的连续函数，norm的定义为$\Vert y{\Vert }_0={\max }_{a⩽x⩽b}|y(x)|$, 因此如果 $y^{\ast }(x)$和 y(x) 的距离为 $\epsilon$，y(x)不会超过 $y^{\ast }(x)$ 上下两个 $\epsilon$ 带的距离
2. ${\mathcal{D}}_1(a,b)$: 即所有 [a,b] 间的含有一阶导的连续函数
   • norm的定义：$\Vert y{\Vert }_1={\max }_{a⩽x⩽b}|y(x)|+{\max }_{a⩽x⩽b}\left|y^{\prime }(x)\right|$.
3. ${\mathcal{D}}_n(a,b)$: 即所有 [a,b] 间的含有一阶导的连续函数
   • norm的定义：$\Vert y{\Vert }_n={\sum }_{i=0}^n{\max }_{a⩽x⩽b}\left|y^{(i)}(x)\right|$

由此，我们可以给出 泛函连续性的定义：

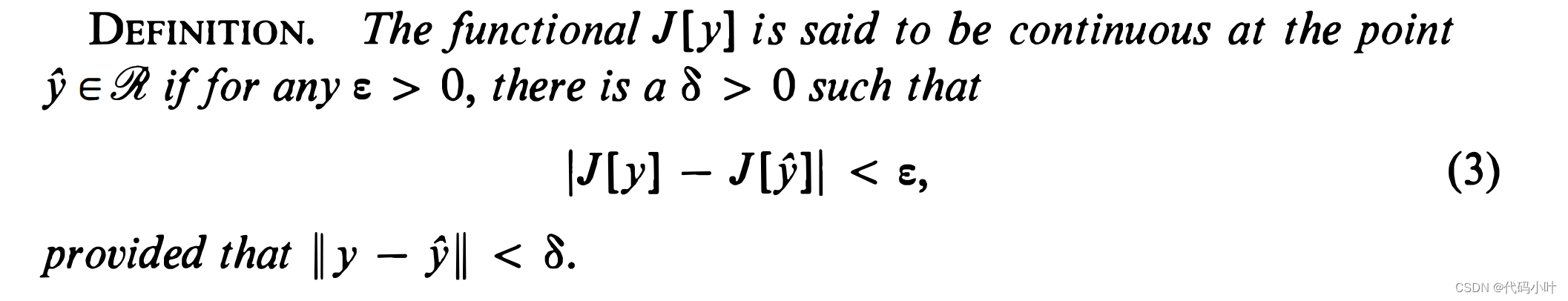
1.3 泛函的变分: 具有极值的必要条件

1. 重要引理/线性泛函的等零条件

这一节我们引出 泛函的变分，类比 n个变量的微分 来 得到结果

1. 线性泛函：首先我们给出线性泛函 的定义

我们给出一个 线性泛函空间的重要例子：

Example 4. More generally, the integral
$$\phi [h]={\int }_a^b\left[{\alpha }_0(x)h(x)+{\alpha }_1(x)h^{\prime }(x)+\cdots +{\alpha }_n(x)h^{(n)}(x)\right]dx,$$
where the ${\alpha }_i(x)$ are fixed functions in $\mathcal{C}(a,b)$, defines a linear functional on ${\mathcal{D}}_n(a,b)$.

${\alpha }_0(x)$ 是一个固定的函数

如果 $\phi [h]$ 为 0，我们会得到什么结果呢，对于${\alpha }_0(x)h(x)$ 的积分，${\alpha }_1(x)h^{\prime }(x)$ 的积分 ，${\alpha }_2(x)h^{\prime \prime }(x)$，以及 $\alpha (x)h(x)+\beta (x)h^{\prime }(x)$我们可以给出一般性的结论

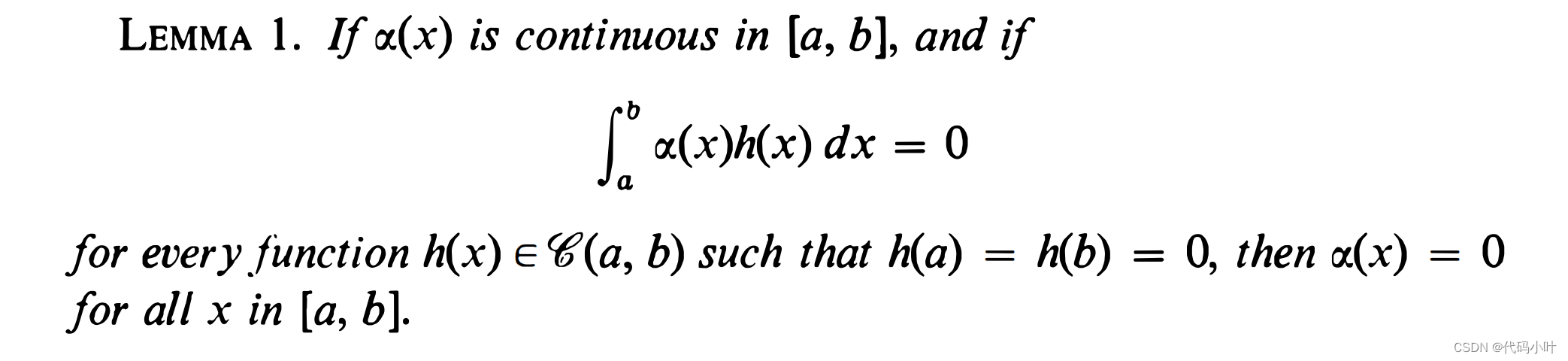
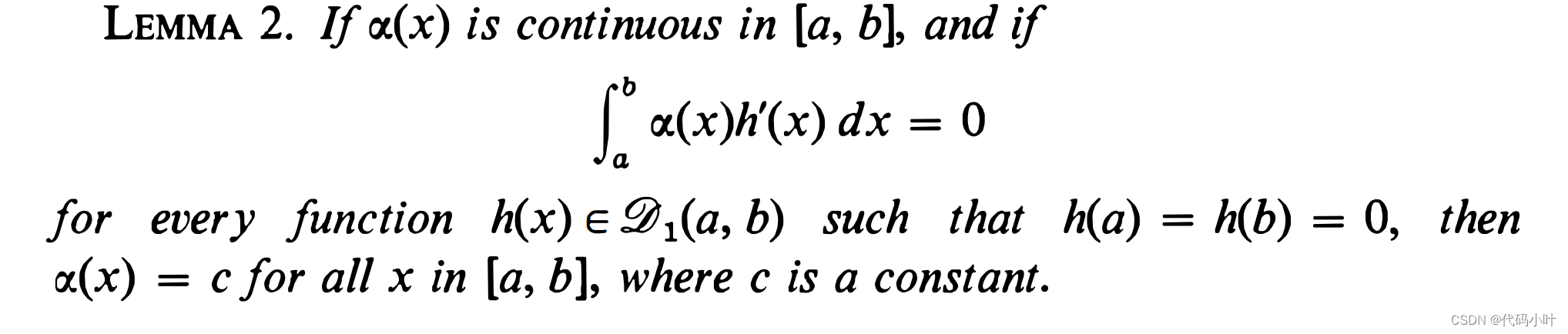
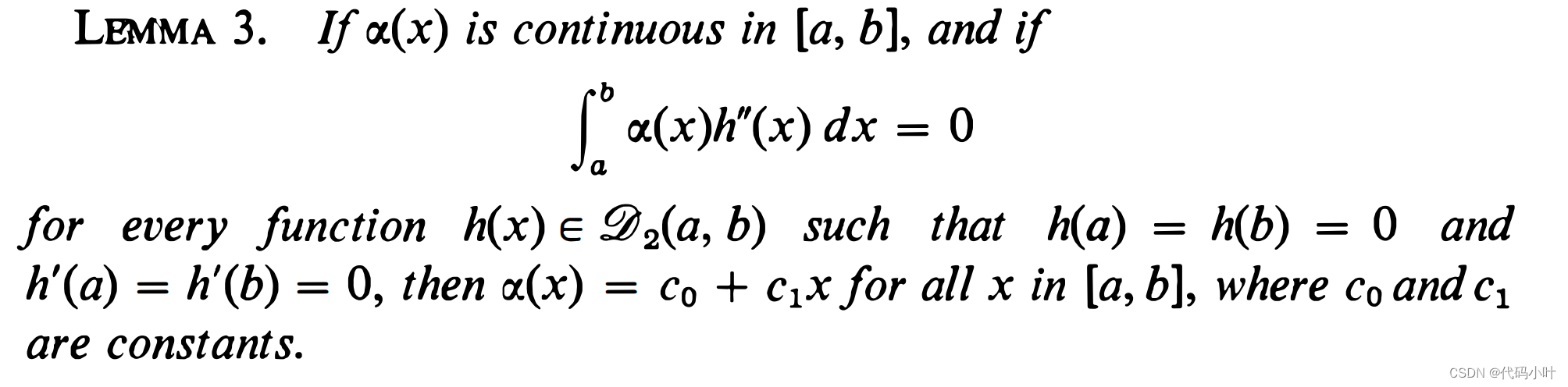
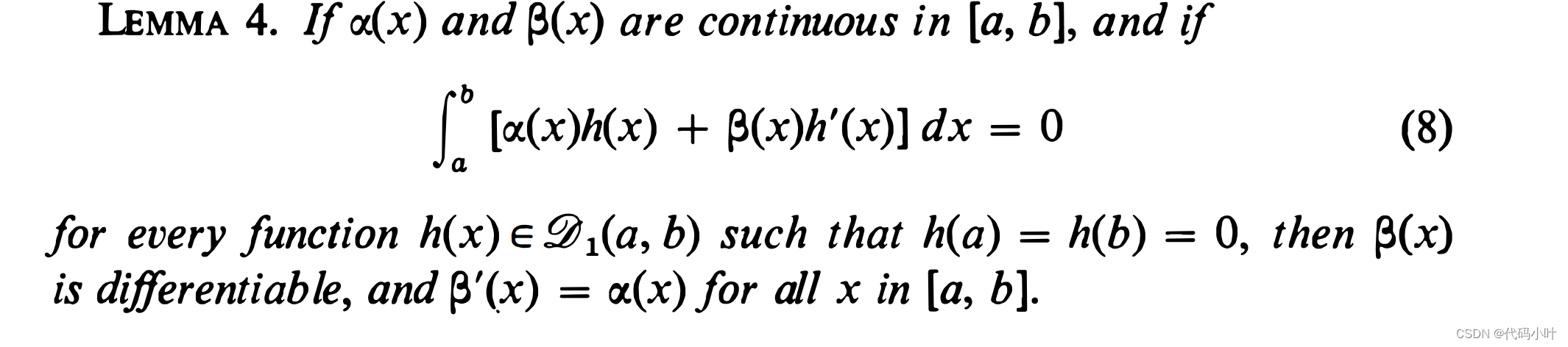
2. 泛函变分

本节类比微积分中 增量与可微的定义，给出 可变分的定义$\delta J[h]$.

1. 定义 泛函$J[y]$的增量 (increment)：
   $\Delta J[h]=J[y+h]-J[y]$
2. 如果我们把y看成固定的，那么 $\Delta J[h]$ 是 h 的泛函
   $\Delta J[h]=\phi [h]+\epsilon \Vert h\Vert$，一般来说他是 非线性的泛函，为了沿用上面的引理我们让$\phi [h]$ 是个 线性泛函，并且 当 $\Vert h\Vert \to 0$ 时，$\epsilon \to 0$，则 $J[y]$ 被称为 可变分的
3. 变分: 线性部分$\phi [h]$ (和增量的差为 比 $\Vert h\Vert$ 的阶数要高的无穷小） 被称作变分，记为$\delta J[h]$

对于变分泛函，以下几个定理是重要:

1. 变分泛函是唯一的
2. 可变分泛函 在 $y=\hat{y}$ 有极值的必要条件是：对于所有 h 有$\delta J[h]=0$

上述定理2的证明如下：

1.4 最简单的变分问题：欧拉方程

本节证明 具有 $J[y]={\int }_a^{b}F\left(x,y,y^{\prime }\right)dx$ 形式的 泛函的解的一般结论。

1. 欧拉方程

我们直接给出问题和结论，并且根据刚刚的变分理论给出证明

1. 方程$F_y-\frac{d}{dx}{F}_{y^{\prime }}=0$被称为欧拉方程
2. 欧拉方程的解被称为 extremal（极值曲线）

2. 证明/欧拉方程的得出

证明如下：

1. 首先写出泛函 J 的增量形式
   $\begin{array}{rl}\Delta J=J[y+h]-J[y]& ={\int }_a^{b}F\left(x,y+h,y^{\prime }+h^{\prime }\right)dx-{\int }_a^{b}F\left(x,y,y^{\prime }\right)dx\\ & ={\int }_a^b\left[F\left(x,y+h,y^{\prime }+h^{\prime }\right)-F\left(x,y,y^{\prime }\right)\right]dx,\end{array}$

2. 根据多元泰勒公式 ，增量可以写为 ${\int }_a^b\left[F_y\left(x,y,y^{\prime }\right)h+F_{y^{\prime }}\left(x,y,y^{\prime }\right)h^{\prime }\right]dx$ 加上一个 h 的高阶无穷小。
   $$\Delta J={\int }_a^b\left[F_y\left(x,y,y^{\prime }\right)h+F_y\left(x,y,y^{\prime }\right)h^{\prime }\right]dx+\cdots$$
   即我们的变分为：

$$\delta J={\int }_a^b\left(F_{y}h+F_{y^{\prime }}{h}^{\prime }\right)dx=0$$

得到
$$F_y-\frac{d}{dx}{F}_{y^{\prime }}=0$$
该式子被称为 欧拉方程

3. 欧拉方程的求解

显然方程是一个 二阶微分方程，他的解通常取决于 A与B点的常数，然而微分方程理论中通常考虑的问题是求解的问题，该解定义在某点的邻域内并满足给定的初始条件(Cauchy’
s problem)。然而，在求解欧拉方程时，我们寻找的解是在所有固定区域上定义的函数，并且满足给定的边界条件。 因此，一个变分得出的微分方程的求解通常不能缩小到现有微分方程的理论上。

因此，我们现在陈述一个由Bernstein 给出的关于的存在唯一性的定理形式的方程 “总体” 解
$y^{\prime \prime }=F\left(x,y,y^{\prime }\right)$

1.5 The Case of Several Variables

多个变量的 泛函定义为如下形式
$$J[z]={\iint }_{R}F\left(x,y,z,z_x,z_y\right)dxdy$$

解如下（原书中有详细证明）

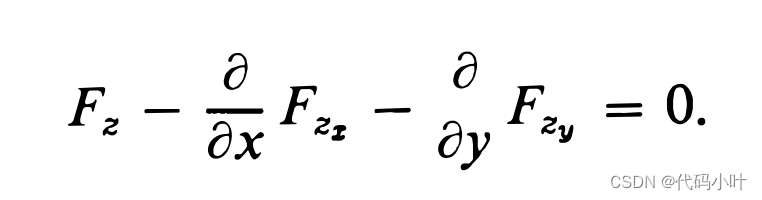
1.6 A Simple Variable End Poi nt Problem

1.7 The Variational Derivative

本节介绍 泛函的变分导数 variational (or functional) derivative $\frac{\delta J}{\delta y}$

1.8 I nvariance of Euler’s Eq u ation

2 一些有用的重要结论/公式/例题

3 习题题解

4 总结