机器学习:基于梯度下降算法的线性拟合实现和原理解析
- 线性拟合
- 梯度下降
- 算法步骤
- 算法实现
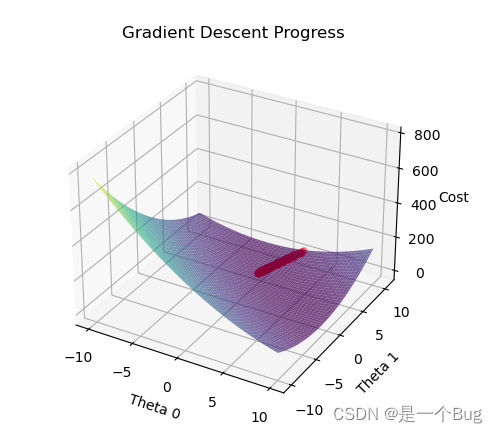
- 数据可视化(动态展示)
- 应用示例
当我们需要寻找数据中的趋势、模式或关系时,线性拟合和梯度下降是两个强大的工具。这两个概念在统计学、机器学习和数据科学领域都起着关键作用。本篇博客将介绍线性拟合和梯度下降的基本原理,以及它们在实际问题中的应用。
线性拟合
线性拟合是一种用于找到数据集中线性关系的方法。它的基本原理是,我们可以使用线性方程来描述两个或多个变量之间的关系。这个方程通常采用以下形式:
y
=
m
x
+
b
y=mx+b
y=mx+b
在这个方程中, y y y 是因变量, x x x 是自变量, m m m 是斜率, b b b 是截距。线性拟合的目标是找到最佳的斜率和截距,以使线性方程最好地拟合数据。
为了找到最佳拟合线,我们通常使用最小二乘法。这意味着我们将所有数据点到拟合线的距离的平方相加,然后寻找最小化这个总和的斜率和截距。这可以用数学优化方法来实现,其中一个常用的方法就是梯度下降。
梯度下降
梯度下降是一种迭代优化算法,用于寻找函数的最小值。在线性拟合中,我们的目标是最小化误差函数,即数据点到拟合线的距离的平方和。这个误差函数通常表示为 J ( m , b ) J(m, b) J(m,b),其中 m m m 是斜率, b b b 是截距。我们的任务是找到 m m m 和 b b b 的值,使 J ( m , b ) J(m, b) J(m,b) 最小化。
梯度下降的基本思想是从一个随机初始点开始,然后根据误差函数的梯度方向逐步调整参数,直到找到局部最小值。梯度下降的迭代规则如下:
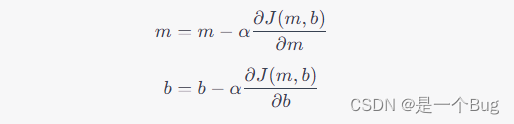
在这里, α \alpha α 是学习率,它决定了每次迭代中参数更新的步长。较大的学习率可能导致快速收敛,但可能会错过最小值,而较小的学习率可能需要更多的迭代。
算法步骤
线性回归中的梯度下降是一种优化算法,用于寻找最佳拟合线性模型的参数,以最小化预测值与实际观测值之间的均方误差(Mean Squared Error,MSE)。梯度下降的原理可以概括为以下几个步骤:
初始化参数: 首先,为线性回归模型的参数(权重和偏置项)选择初始值。通常,可以随机初始化这些参数。
计算损失函数: 使用当前的参数值,计算出模型的预测值,并计算预测值与实际观测值之间的差异,即损失函数。在线性回归中,常用的损失函数是均方误差(MSE),它表示为:
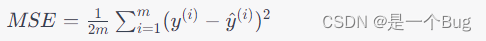
其中, m m m 是样本数量, y ( i ) y^{(i)} y(i) 是第 i i i 个观测值, y ^ ( i ) \hat{y}^{(i)} y^(i) 是模型的预测值。
计算梯度: 梯度是损失函数关于参数的偏导数,表示了损失函数在参数空间中的变化方向。梯度下降算法通过计算损失函数关于参数的梯度来确定参数更新的方向。对于线性回归模型,梯度可以表示为:
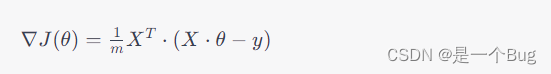
其中, J ( θ ) J(\theta) J(θ) 是损失函数, θ \theta θ 是参数向量, X X X 是特征矩阵, y y y 是目标向量。
参数更新: 使用梯度信息,按照下面的规则来更新参数:
θ = θ − α ∇ J ( θ ) θ=θ−α∇J(θ) θ=θ−α∇J(θ)
其中, α \alpha α 是学习率,它控制着每次参数更新的步长。学习率越小,参数更新越小,但收敛可能会更稳定。学习率越大,参数更新越快,但可能会导致不稳定的收敛或发散。
重复迭代: 重复执行步骤2至步骤4,直到满足停止条件,例如达到最大迭代次数或损失函数收敛到一个足够小的值。在每次迭代中,参数都会根据梯度信息进行更新,逐渐优化以减小损失函数。
梯度下降的目标是找到损失函数的最小值,这将使线性回归模型的预测值与实际观测值之间的误差最小化。通过不断调整参数,梯度下降可以使模型逐渐收敛到最佳参数值,从而得到最佳拟合线性模型。
算法实现
import numpy as np
import matplotlib.pyplot as plt
# 设置字体为支持汉字的字体(例如宋体)
plt.rcParams['font.sans-serif'] = ['SimSun']
# 创建示例数据
X = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])
# 添加偏置项(截距项)到特征矩阵
# 添加了偏置项(截距项)到特征矩阵 X。这是通过在 X 前面添加一列全为1的列来实现的。这是线性回归模型中的常见步骤。
X_b = np.c_[np.ones((len(X), 1)), X.reshape(-1, 1)]
# 使用正规方程计算最佳参数
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
# 使用梯度下降计算最佳参数
def gradient_descent(X_b, y, theta, learning_rate, num_epochs):
m = len(y)
losses = []
for epoch in range(num_epochs):
# 计算当前参数下的预测值。
predictions = X_b.dot(theta)
error = predictions - y
# 计算均方误差(MSE)作为损失函数,衡量预测值和实际值之间的差异。
loss = np.mean(error**2)
# 计算损失函数的梯度,用于更新参数。
# X_b.T 表示矩阵 X_b 的转置。在线性代数中,矩阵的转置是指将矩阵的行和列交换,即将矩阵的列向量变成行向量,反之亦然。
gradient = 2 * X_b.T.dot(error) / m
theta -= learning_rate * gradient
losses.append(loss)
return theta, losses
theta = np.random.randn(2)
learning_rate = 0.01
num_epochs = 1000
theta, losses = gradient_descent(X_b, y, theta, learning_rate, num_epochs)
# 可视化数据和拟合结果
plt.scatter(X, y, label='数据点')
plt.plot(X, X_b.dot(theta_best), label='正规方程拟合', color='green')
plt.plot(X, X_b.dot(theta), label='梯度下降拟合', color='red')
plt.xlabel('特征值')
plt.ylabel('目标值')
plt.legend()
plt.show()
数据可视化(动态展示)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# 创建一些示例数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.rand(100, 1)
# 初始化线性模型参数
theta = np.random.randn(2, 1)
def gradient_descent(X, y, theta, learning_rate, num_iterations):
m = len(y)
history = []
for iteration in range(num_iterations):
gradients = -2/m * X.T.dot(y - X.dot(theta))
theta -= learning_rate * gradients
history.append(theta.copy())
return history
learning_rate = 0.1
num_iterations = 50
# 添加偏置项
X_b = np.c_[np.ones((100, 1)), X]
# 执行梯度下降算法并获取参数历史
parameter_history = gradient_descent(X_b, y, theta, learning_rate, num_iterations)
# 创建动态可视化
fig, ax = plt.subplots()
line, = ax.plot([], [], lw=2)
def animate(i):
y_pred = X_b.dot(parameter_history[i])
line.set_data(X, y_pred)
return line,
ani = FuncAnimation(fig, animate, frames=num_iterations, interval=200)
plt.scatter(X, y)
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression with Gradient Descent')
plt.show()
应用示例
线性拟合和梯度下降在各种领域都有广泛的应用。以下是一些示例:
股市预测:通过线性拟合历史股票价格数据,可以尝试预测未来股价的趋势。
房价预测:使用线性拟合来估算房屋价格与特征(如面积、位置等)之间的关系,帮助买家和卖家做出决策。
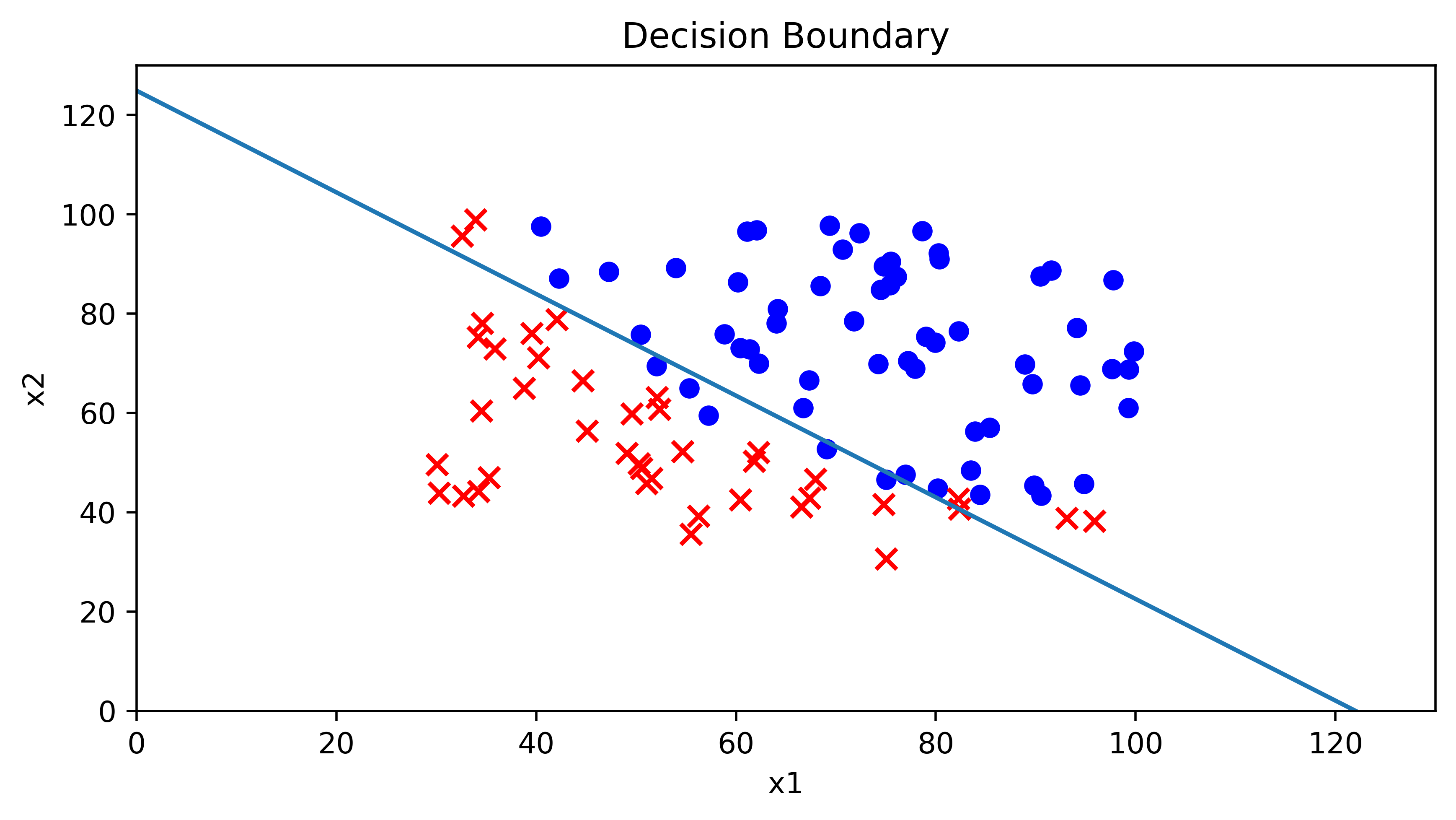
机器学习模型训练:梯度下降是训练线性回归、逻辑回归和神经网络等机器学习模型的关键步骤。
自然语言处理:在自然语言处理中,线性拟合可以用于情感分析和文本分类任务。
总之,线性拟合和梯度下降是数据科学和机器学习领域的基本工具,它们帮助我们理解数据中的关系,并训练模型以做出预测和决策。这两个概念的理解对于处理各种数据分析和机器学习问题都至关重要。希望本博客能够帮助你更好地理解它们的基本原理和应用。