通过上一节我们知道顺序表的优点:
可随机存储(O(1)):查找速度快
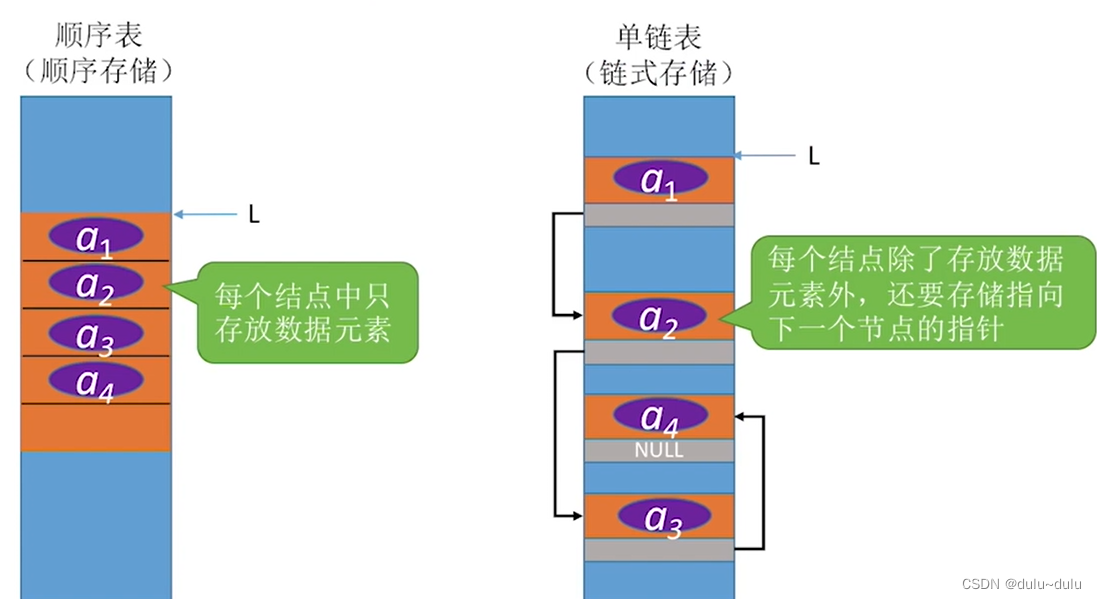
存储密度高:每个结点只存放数据元素,而单链表除了存放数据元素之外,还需存储指向下一个节点的指针
http://t.csdn.cn/p7OQf
但是顺序表也有明显的缺点,就是需要大片的连续空间,改变容量不方便,所以出现了单链表
目录
一.初始化单链表
二.插入结点
1.带头结点的插入
2.不带头结点的插入:不存在第’0‘个结点,因此i=1时,需要特殊处理
补充:带头结点
指针结点的后插操作
指针的前插操作
三.删除结点
1.带头节点的删除
2.不带头节点的删除
3.删除指定节点
四.单链表的查找
1.按位查找:查找第i个节点的值
2.按值查找:查找链表中是否有元素e
补充:求表的长度
一.初始化单链表
typedef struct LNode{
ElemType data; //每个节点存放一个数据元素
struct LNode *next;//指针指向下一个节点
}LNode,*LinkList;
//这里的LinkList==》typedef struct LNode *LinkList,定义一个指向结构体的指针
//在这里
//LNode *L与LinkList L;//都是表示指向单链表第一个节点的指针
//LNode *L强调的是一个节点
//LinkList L强调的是一个单链表
/*不带头节点的单链表
bool InitList(LinkList &L)
{
L=NULL;//防止空间中存在脏数据
return true;
}
bool Empty(LinkList L)
{
return (L=NULL);
}
void test()
{
LinkList L;
InitList(L);
}
*/
//带头结点的单链表
LinkList InitList(LinkList &L)
{
L=(LNode *)malloc(sizeof(LNode));//分配一个头结点
if(L==NULL)
return NULL;
L->next=NULL;//声明一个指向单链表的指针
return L;
}
bool Empty(LinkList L)
{
if(L->next==NULL)
{
return true;
}
else
return false;
}
//我们可以把头结点看作第0个结点,这样写代码更加方便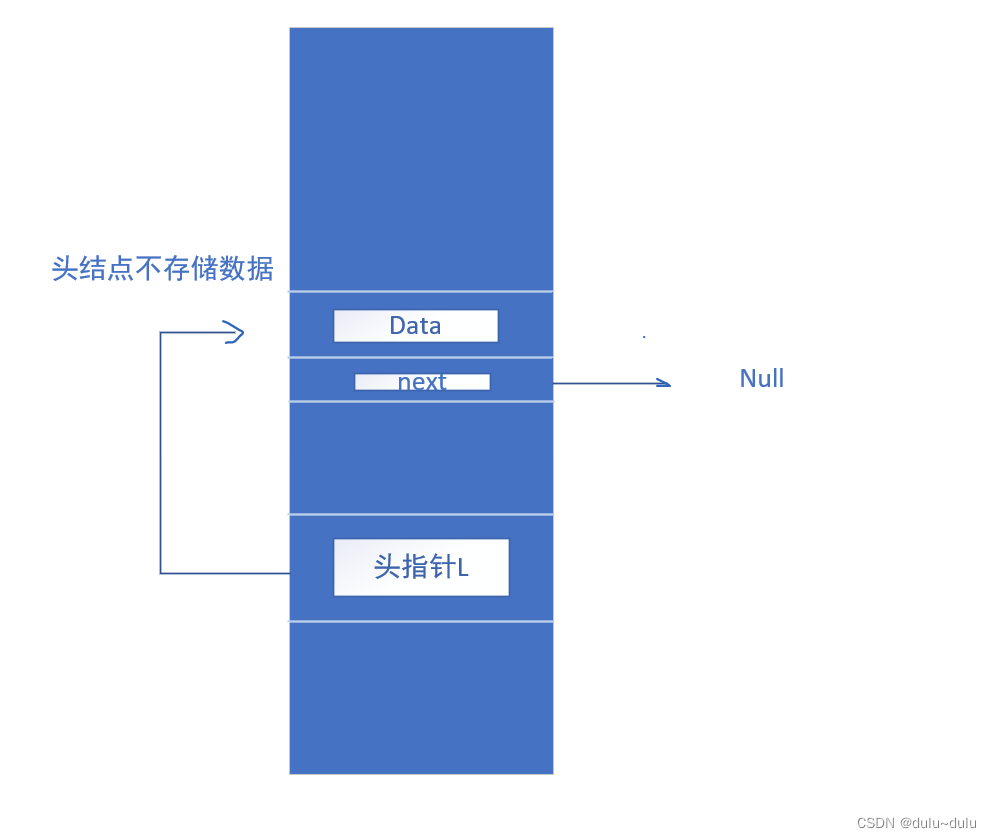
二.插入结点
1.带头结点的插入
bool ListInsert(LinkList &L,int i,ElemType e)//i表示插入的位置,e表示插入的元素
{
if(i<1)
{
return false;
}
LNode *p;//指针p指向当前扫描到的结点
int j=0;//当前p指向的是第几个结点
p=L; //指向头节点,头节点是第0个节点
while(p!=NULL && j<i-1)//循环找到第i-1个结点
{
p=p->next;
j++;
}
if(p==NULL)
{
return false;
}
LNode *s=(LNode *)malloc(sizeof(LNode));
s->data=e;
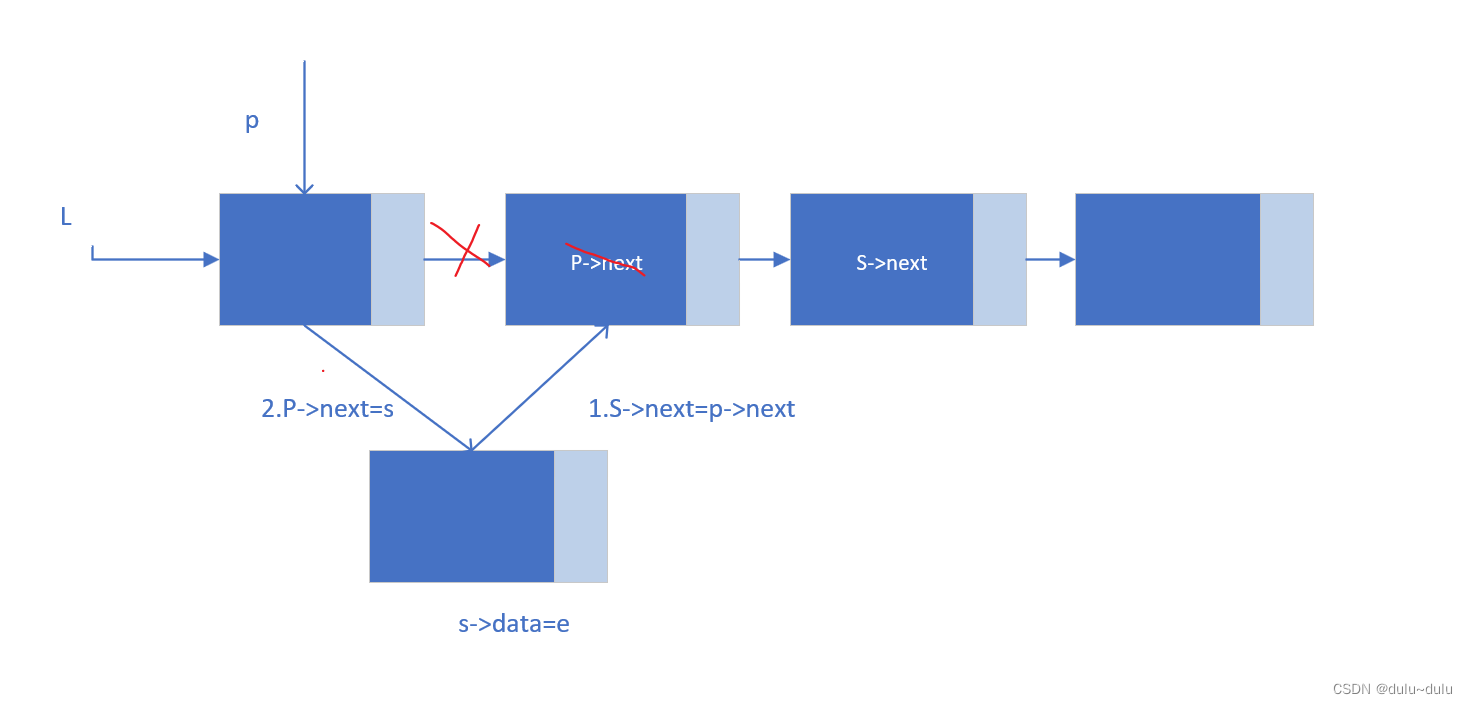
s->next=p->next;
p->next=s;
return true;
}
若先p->next=s,再s->next=p->next,即
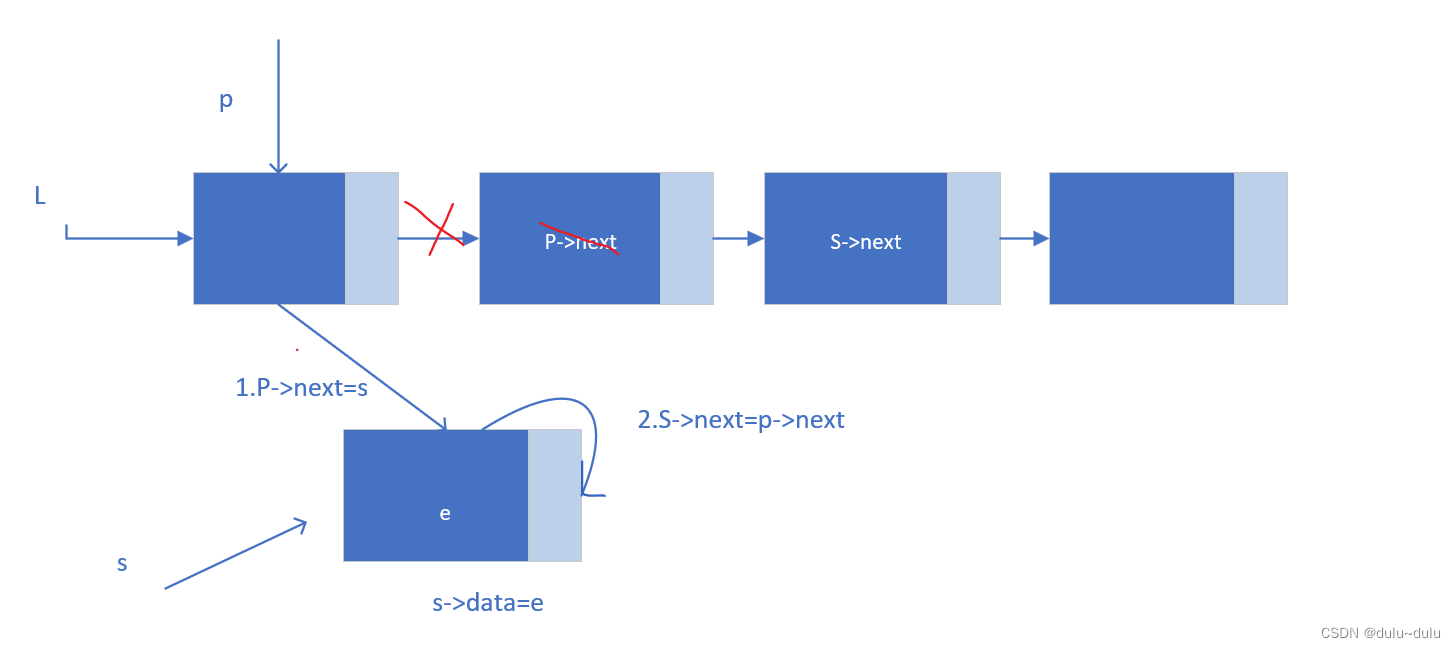
带头结点的插入
最好情况:插在表头O(1)
最坏情况:插在表尾O(n)
平均情况:O(n)
2.不带头结点的插入:不存在第’0‘个结点,因此i=1时,需要特殊处理
bool ListInsert(LinkList &L,int i,ElemType e)
{
if(i<1)
return false;
if(i==1)//插入第1个结点的操作与其他节点操作不同
{
LNode *s=(LNode *)malloc(sizeof(LNode));
s->data=e;
s->next=L;
L=s;//头指针指向新结点
return true;
}
LNoden *p;
int j=1;//除了这里j=1和带头结点的指针不同,其他是相同的
p=L;
while(p!=NULL && j<i-1)
{
p=p->next;
j++;
}
if(p==NULL)
{
return false;
}
LNode *s=(LNode *)malloc(sizeof(LNode));
s->data=e;
s->next=p->next;
p->next=s;
return true;
}
删除第一个元素时,需要更改头指针L
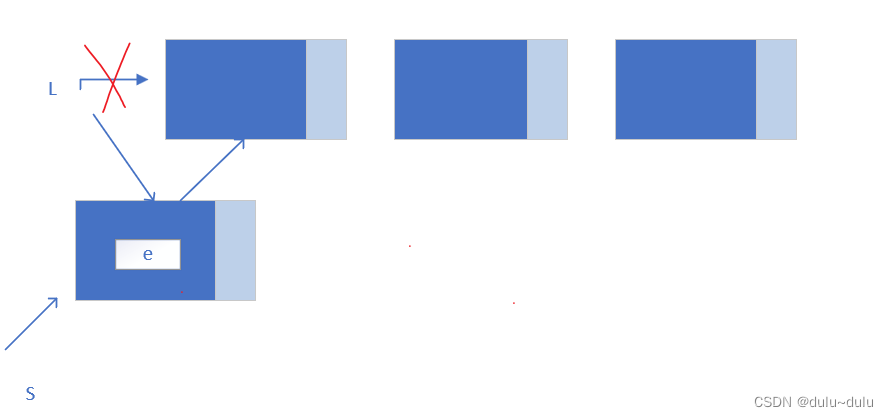
补充:带头结点
指针结点的后插操作
//在p结点之后,插入元素e
bool InsertNextNode(LNode *p,ElemType e)
{
if(p==NULL)
return false;
LNode *s=(LNode *)malloc(sizeof(LNode));
if(s=NULL)//如果内存分配失败,如内存不足等
return false;
s->data=e;
s->next=p->next;
p->next=s;
return true;
}指针的前插操作
1.第一种方法:通过前驱节点完成前插操作
需要传入头节点才能找到p的前驱结点,即
bool InsertPriorNode(LinkList L,LNode *p,ElemType e)
bool InsertPriorNode(LinkList L,LNode *p,ElemType e)
{
if(p==NULL)
return false;
LNode *s=(LNode*)malloc(sizeof(LNode));
if(s==NULL)
return false;
LNode *current=L;
while(current->next!=p)
current=current->next;
s->data=e;
s->next=current->next;
current->next=s;
return true;
}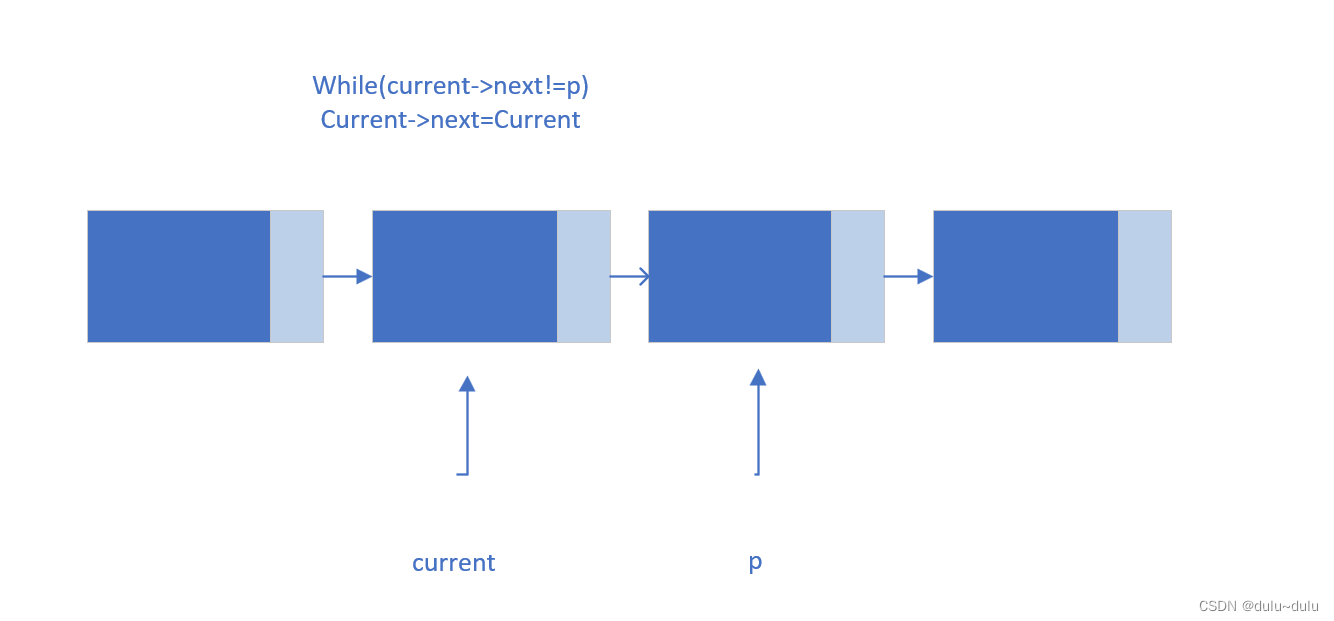
在这里时间复杂度为O(n),如何减小时间复杂度,可以用第二种方法
2.第二种方法:通过结点的数据交换完成前插操作
bool InsertPriorNode(LNode *p,ElemType e)
{
if(p==NULL)
return false;
LNode *s=(LNode *)malloc(sizeof(LNode));
if(s==NULL)
return false;
s->next=p->next;
p->next=s; //新节点s连到p之后
s->data=p->data;//将p中元素复制到s中
p->data=e;//p中元素覆盖为e
return true;
}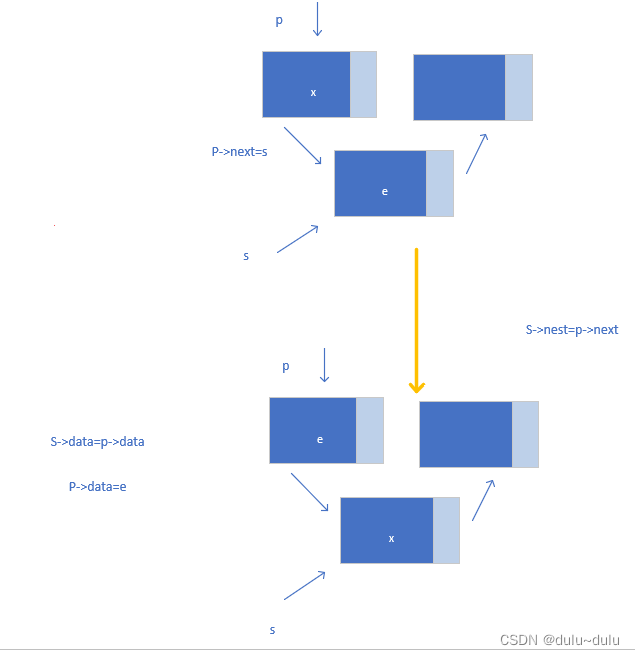
关键在于s->data=p->data;p->data=e;这样实现了两节点的数据交换,实现了在p结点前插入e元素,同时这里的时间复杂度是O(1)
所以对于插入节点可以观察到如下两个规律
1.先后再前
s->next=p->next;
p->next=s;
2.先小后大
在第一个节点插入
s->next=L;
L=s //头指针指向新插入的节点s
三.删除结点
1.带头节点的删除
bool ListDelete(LinkList &L,int i,ElemType &e)
{
if(i<1)
{
return false;
}
LNode *p=L;
int j=0;
while(p!=NULL && j<i-1)//这里是寻找要删除结点的前驱结点
{
p=p->next;
j++;
}
if(p==NULL)
return false;
if(p->next==NULL)//如果要删除结点的前驱结点为NULL,那么删除就无意义了
return false;
LNode *q=p->next;//令q指向被删除结点
e=q->data;//用e返回元素的值
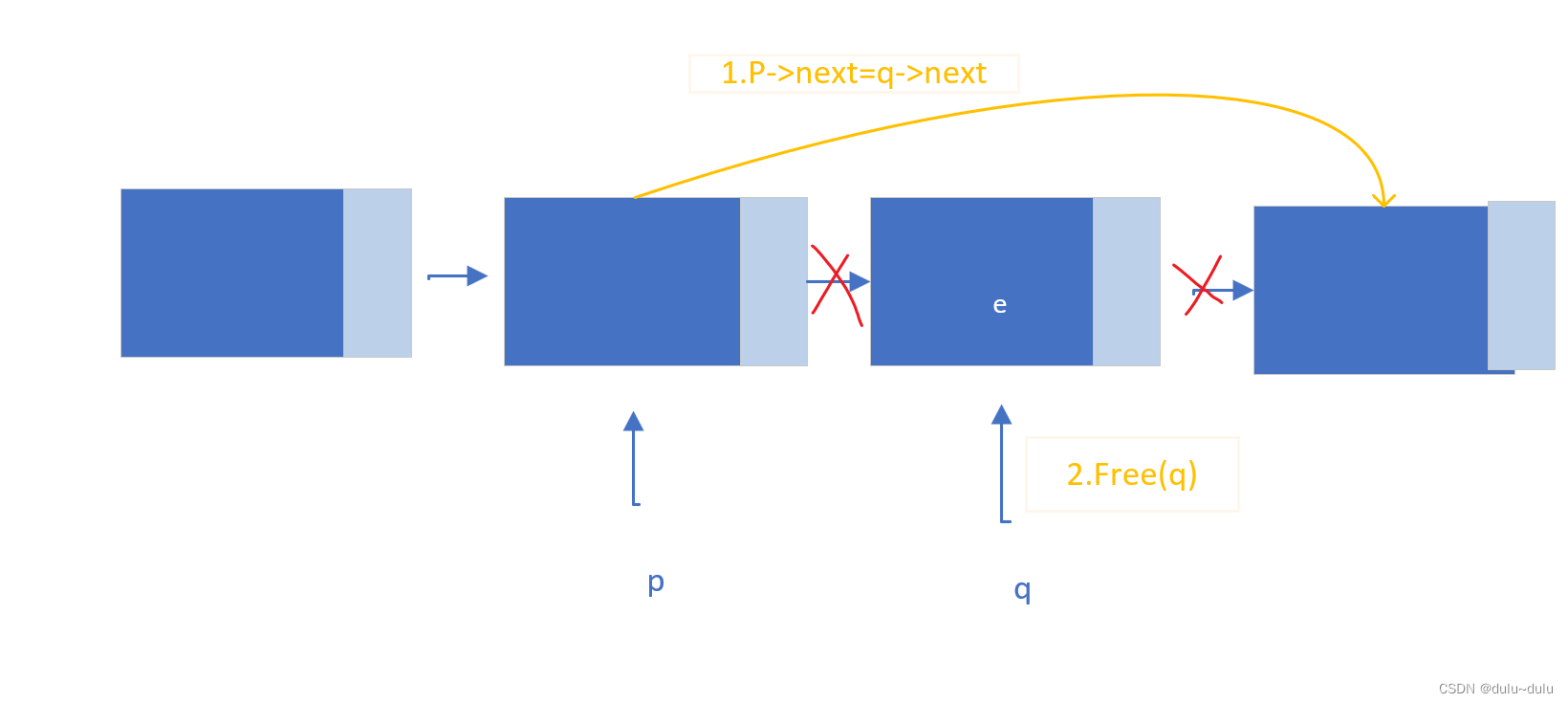
p->next=q->next;//将*q结点从链表中断开
free(q);//释放q
return true;
}
最好时间复杂度为O(1):删除第一个节点
最坏和平均时间复杂度为O(n)
2.不带头节点的删除
bool ListDelete(LinkList& L, int i, ElemType& e) {
if (i < 1)
return false;
if (i == 1) {
LNode* p = L;
L = L->next;
free(p);
return true;
}
LNode* p = L;
int j = 1;
while (p != NULL && j < i - 1) {//寻找删除节点的前驱节点
p = p->next;
j++;
}
if (p == NULL || p->next == NULL)
return false;
LNode* q = p->next;
e = q->data;
p->next = q->next;
free(q);
return true;
}
3.删除指定节点
//删除指定节点p
bool DeleteNode(LNode *p)
{
if(p==NULL)
return false;
LNode *q=p->next; // 令q指向*p的后继节点
q->data=p->next->data;
p->next=q->next;//将*q节点从链中断开
free(q);//释放后继节点的存储空间
return true;
}
//如果p的后继节点刚好为NULL,那么p->next->data指向空所以这段代码对此情况不适用
//针对此情况还是要找到其前驱节点,然后进行删除找前驱节点进行删除
bool DeleteNode(LinkList L, LNode* p, ElemType& e) {
if (p == NULL)
return false;
LNode* q = L;
while (q->next != p)
q = q->next;
q->next = NULL;
e = p->data;
free(p);
return true;
}四.单链表的查找
1.按位查找:查找第i个节点的值
LNode *GetElem(LinkList L,int i)
{
if(i<0)
return false;
LNode *p=L;
int j=0;
while(p!=NULL && j<i)//循环找到第i个节点
{
p=p->next;
j++;
}
return p;
}
平均时间复杂度O(n)
2.按值查找:查找链表中是否有元素e
LNode *LocateElem(LinkList L,ElemType e)
{
LNode *p=L->next;
//从第一个节点开始查找数据域为e的节点
while(p!=NULL && p->data!=e)
p=p->next;
return p;//找到后返回该节点的指针,否则为NULL
}平均时间复杂度O(n)
补充:求表的长度
int length(LinkList L)
{
int len=0;
LNode *p=L;
while(p!=NULL){
p=p->next;
len++;
}
return len;
}