1.预备概念
1.1 后验分布
最大后验(Maximum a Posteriori,MAP)概率估计详解
【参考文章】https://blog.csdn.net/fq_wallow/article/details/104383057
1.2 重参数 Reparameterization
目的是:
转为公式表达从而实现微分
知乎上的解读
csdn上的解读
证明了变分下界的重新参数化产生了一个下界估计量
通过使用所提出的下界估计将近似推理模型(也称为识别模型)拟合到难处理的后验数据集,对于后验推理可以特别有效
1.3 蒙特卡洛法
【参考文章】https://blog.csdn.net/uujjjj/article/details/125596713
1.4变分贝叶斯初探
【参考文章】https://www.jianshu.com/p/86c5d1e1ef93
1.5 概率论中PDF、PMF和CDF的区别与联系
【参考文章】https://blog.csdn.net/Anne033/article/details/114327608
1.6 贝叶斯
1.7 Auto-Encoding
1.8 KL散度
(1)熵
(2)交叉熵 : 用基于P的编码去编码来自Q的样本,所需要的比特个数
(3)kl
2. Auto-Encoding Variational Bayes
【参考】变分贝叶斯初探
贝叶斯公式中如下:
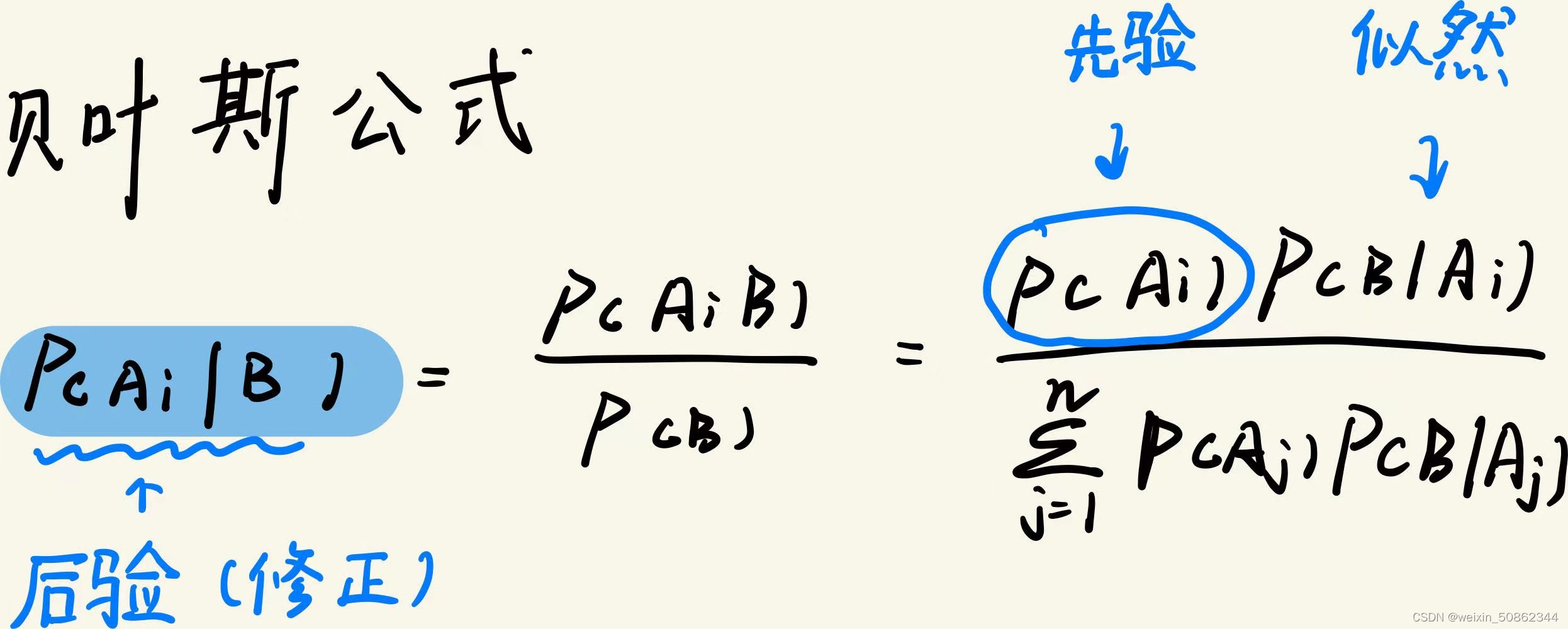
但是这样对先验和似然的理解不够直观,来看一道《概率论》里面的题目:
对以往数据分析表明,当机器状态良好时,产品的合格率为98%,而当机器发生故障时,产品的合格率为55%。某天早上机器开动时,其状态良好的概率为95%。试求某日早上第一件产品是合格,平时机器状态为良好的概率?(答案是97%)
公式很简单,就不给出来了。在这道题中:
(1)先验:产品的合格率为98%
(2)似然:某天早上机器开动时,其状态良好的概率为95%
(3)要求的就是后验
后验其实就是通过修正先验获得更好的结果,但是实际上似然和先验并不是明确可以知晓的,因此是通过拟合后验分布从而来得到。
2.1 变量
将变量分成两类:可观察变量和不可观察变量
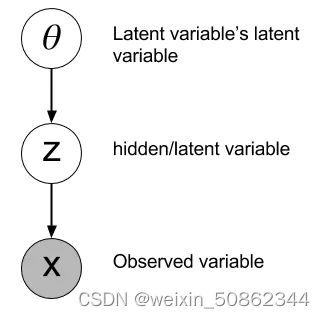
2.2 The variational bound变分下界
Q(z)即为拟合得到的分布
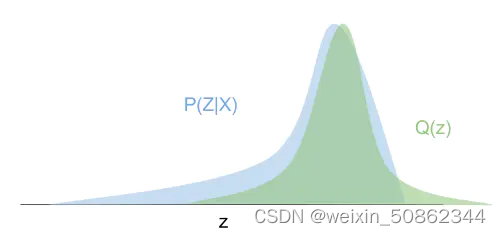
图片来自变分贝叶斯初探
使用KL散度来度量两个分布的距离(损失函数)
KL散度:
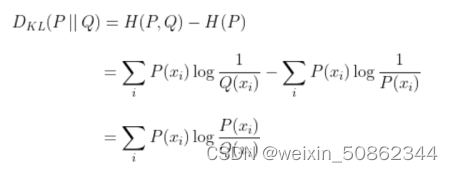
在当前这个式子中
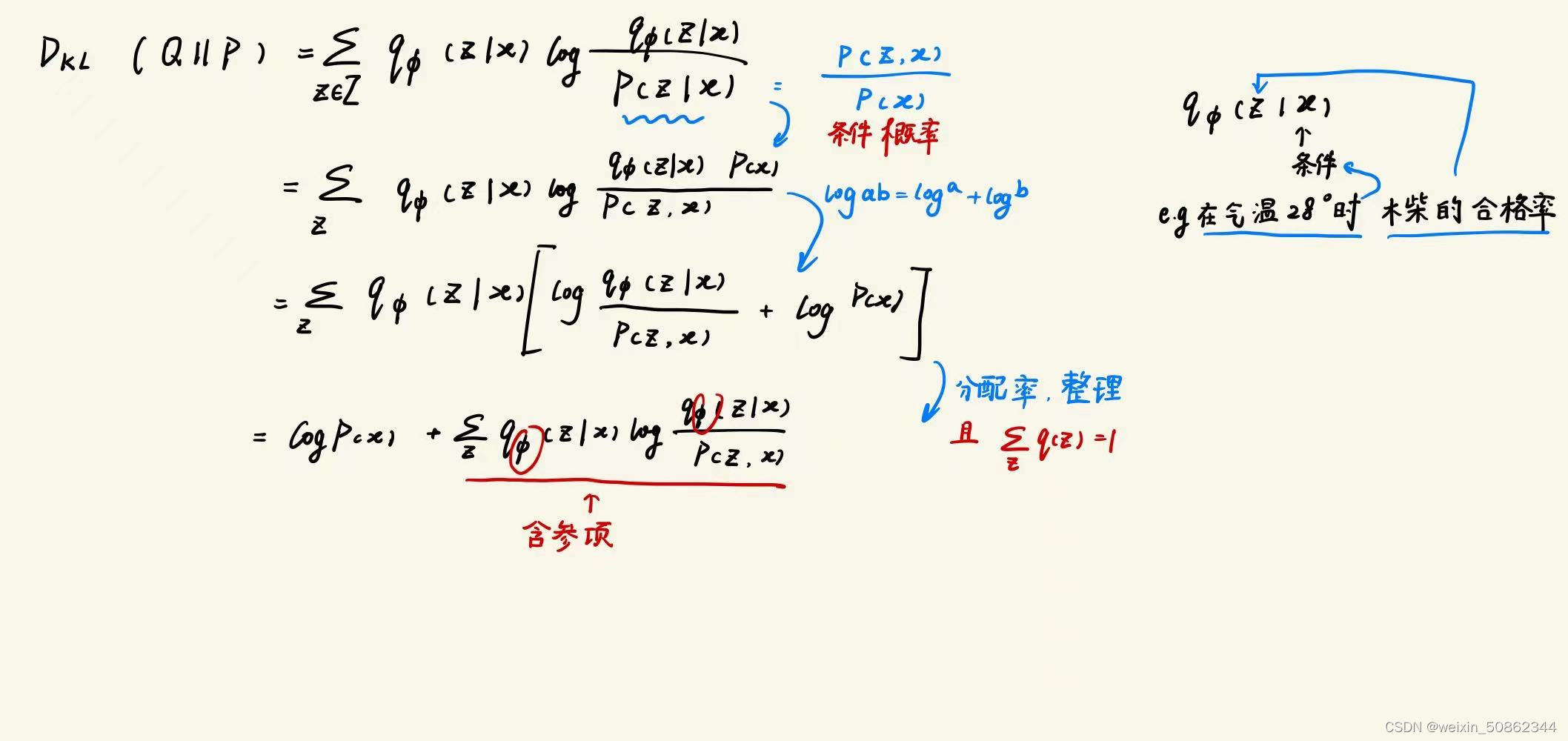
想要使拟合的分布尽可能趋近于后验分布,此时就希望后验分布和拟合分布的kl散度尽可能小,因此我们要最小化含参项

因为kl散度一定是大于等于0的,logP(X)也应该是大于0的,其实L就是logP(x)的下界,因此就单拎出来作为变分下界。
论文中的公式如下(theta:隐变量的参数,φ:拟合分布的参数):
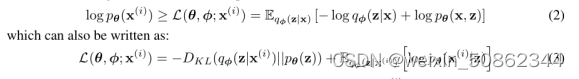
想要对这两个参数进行优化从而最小化L。
但是对φ优化会有问题,表现为方差过大。按我的理解是: (和下图一样)φ也是隐变量的潜在变量,z不可见的情况下,只能通过采样Z来“猜测”φ的分布,因为采样所以是不可微的

2.3 The SGVB estimator and AEVB algorithm
不进行采样而是替换成使用(辅助)噪声变量的可微变换,相当于将这个过程转化成为了映射过程。随机性从原先的φ转移到了随机噪声

从而可以使用随机梯度下降等优化方法
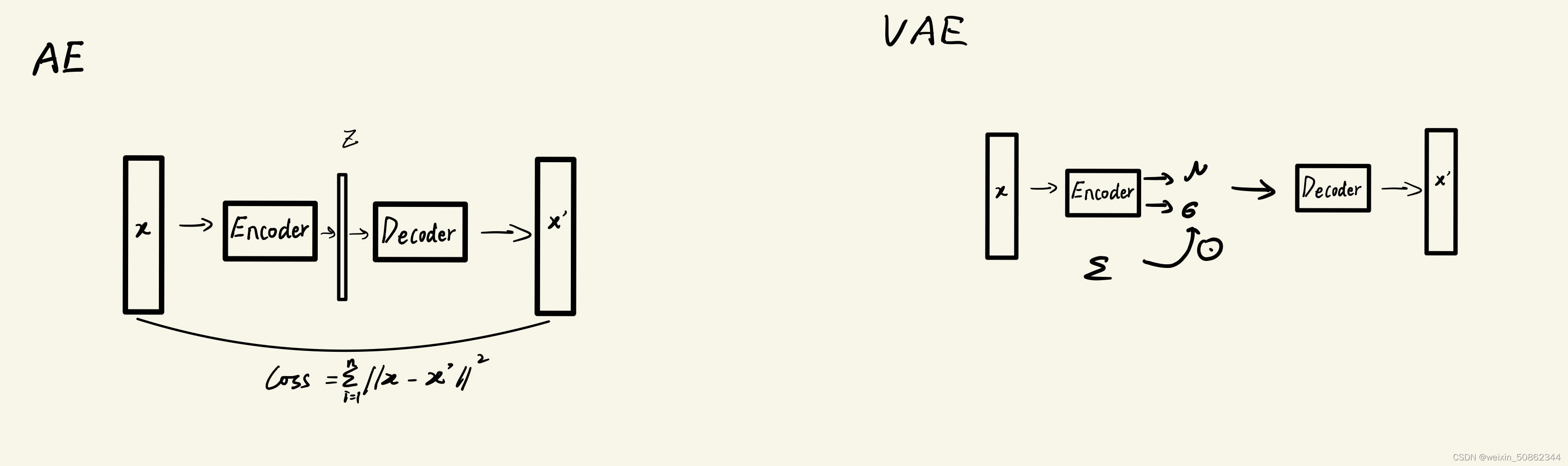
2.4 VAE