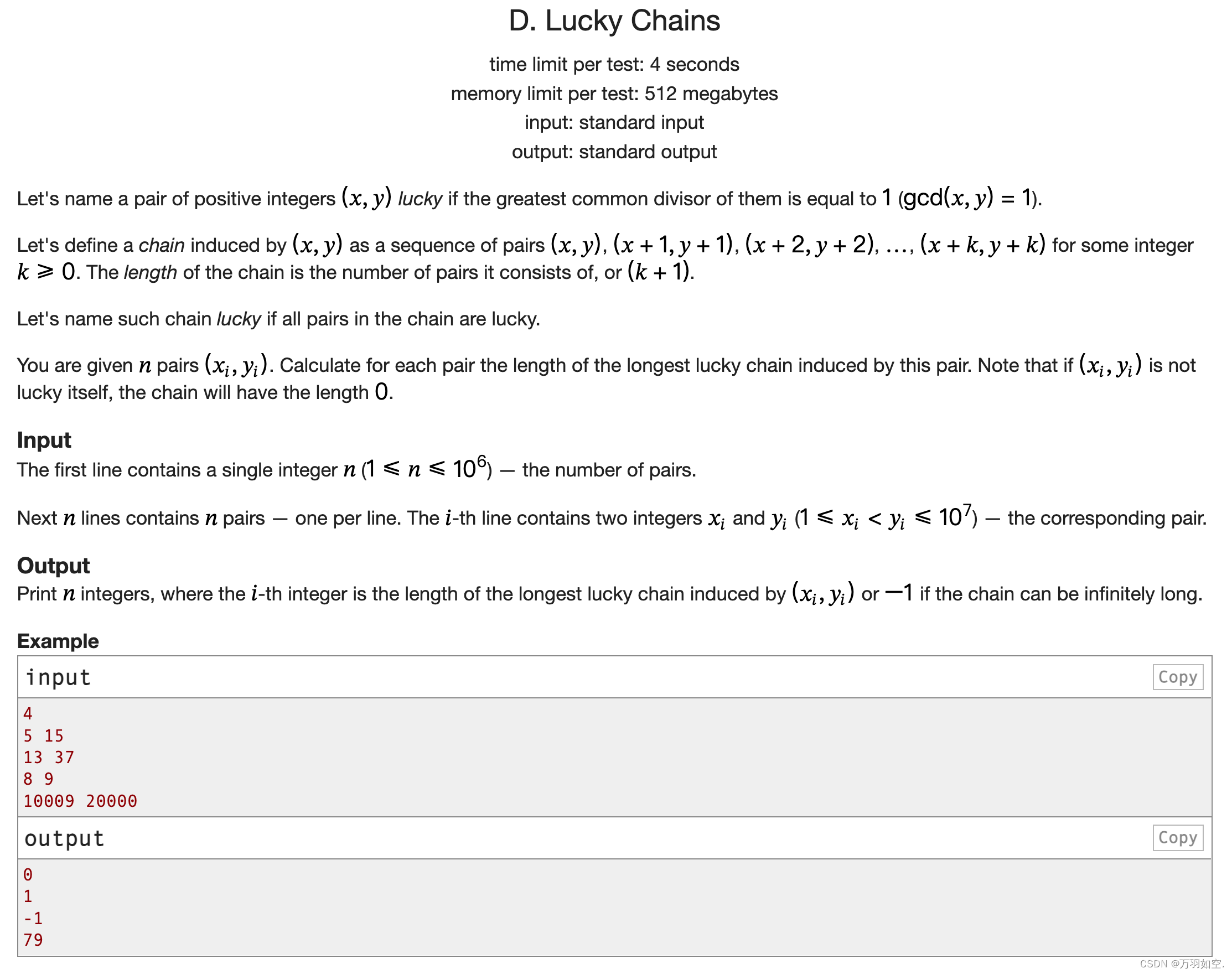
翻译：

让我们命名一对正整数(𝑥，𝑦)，幸运的是它们的最大公约数等于1 (gcd(𝑥，𝑦)=1)。

让我们定义一个链(𝑥𝑦)引起的一系列双(𝑥𝑦),(𝑥+ 1,𝑦+ 1)(𝑥+ 2,𝑦+ 2),……(𝑥+𝑘𝑦+𝑘)对于一些整数𝑘≥0。链的长度是由它组成的对的数量，或(𝑘+1)。

如果链上的所有对都是幸运的，我们就把这个链命名为幸运链。

您将得到𝑛对(𝑥𝑖，𝑦𝑖)。计算每一对由这对引出的最长幸运链的长度。注意，如果(𝑥𝑖，𝑦𝑖)本身不是幸运的，链的长度将为0。

输入
第一行包含一个整数𝑛(1≤𝑛≤106)-配对的数量。

接下来的𝑛行包含𝑛对——每行一个。𝑖-th行包含两个整数𝑥𝑖和𝑦𝑖(1≤𝑥𝑖<𝑦𝑖≤107)—对应的一对整数。

输出
打印𝑛整数，其中𝑖-th整数是由(𝑥𝑖，𝑦𝑖)或−1(如果链可以无限长)诱导的最长幸运链的长度。

例子
inputCopy
4
5 15
13 37
8 9
10009 20000
outputCopy
0
1
－1
79
请注意
在第一个测试用例中，gcd(5,15)=5>1，所以它已经不是幸运的，所以幸运链的长度是0。

在第二个测试案例中，gcd(13+1,37+1)=gcd(14,38)=2。所以，幸运链由一对(13,37)组成。 

思路：0 1 -1，这三种情况都可以直接判断掉。所以我们直接看后边的，最近总是看错题，看错样例，这场看这道题的时候已经没多少时间了，稍微想了下，然后糊了下代码。没过去，过去就不正常了。 b>a时，gcd（a,b）=gcd(a,b-a),为什么可以这样写呢？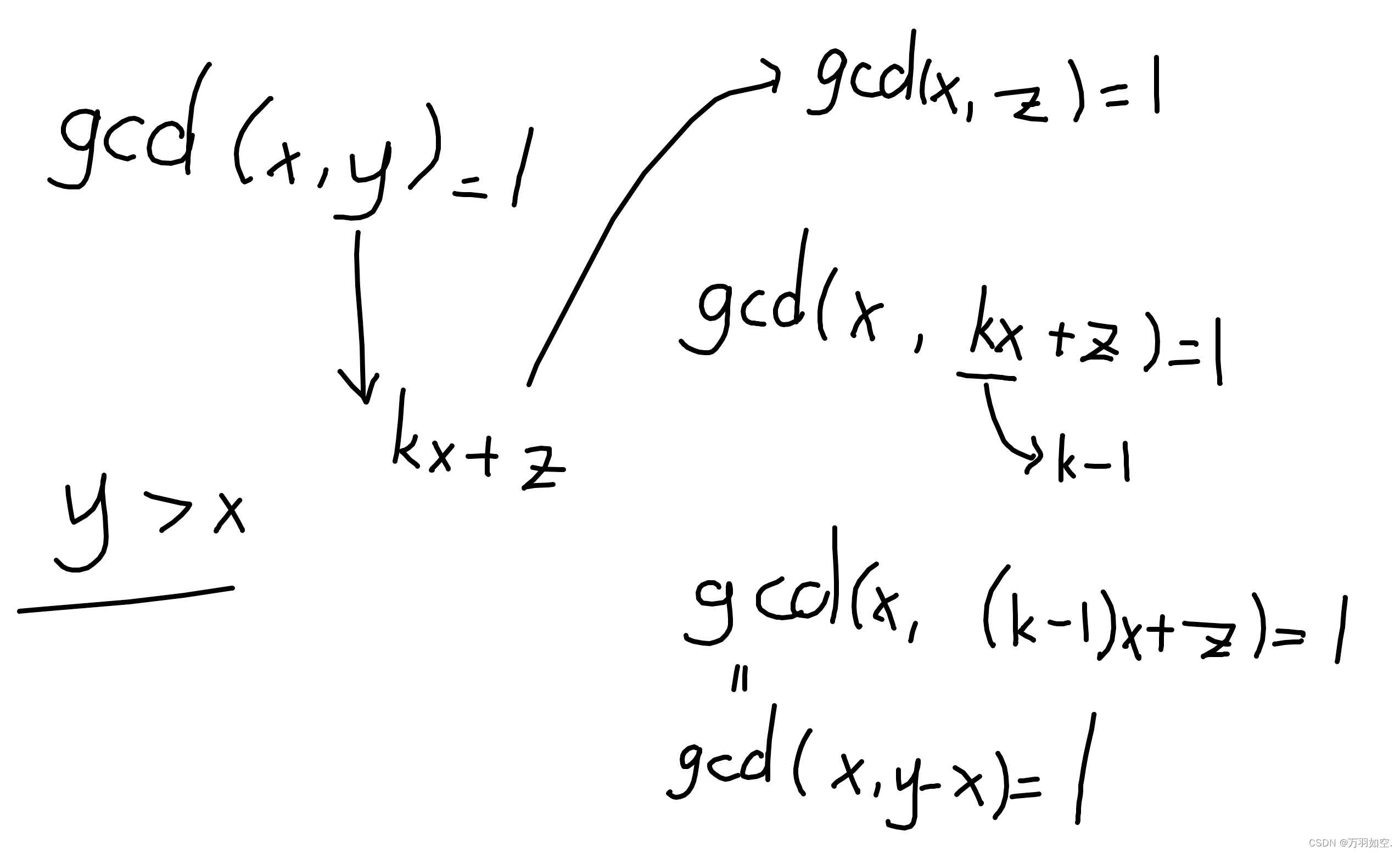

大概证明过程时这样，写的有点乱（ 惨不忍睹，所以我们可以得到gcd(a+x,b+x)==gcd(a+x,b-a)。

这时候我们就发现了，b-a是一个定植，然后a不断+x，我们就可以来分解枚举 b-a的质因子，来每次看a+x到达其倍数，需要加上的值，然后取最小即可。（需要注意优化，代码很容易T掉wwwww

代码：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
bool vis[10000005];
vector<int>prime;
void get_prime(int x){
    for (int i =2; i<=x; i++) {
        if (!vis[i]) {
            prime.push_back(i);}
            for (int j=0; j<prime.size()&&prime[j]*i<=x; j++) {
                vis[prime[j]*i]=true;
                if (i%prime[j]==0) {
                    break;
                }
            }
    }
}

int x,y;
void solv(){
    cin>>x>>y;
    if (x>y) {
        swap(x, y);
    }
    
    if (gcd(x, y)!=1) {
        printf("0\n");return;
    }
    if (x%2==1&&y%2==1) {
        printf("1\n");return;
    }
    if (x+1==y) {
        printf("-1\n");return;
    }
    int kl=y-x;
    int an=1e7+5;
    for (int i =0; i<prime.size()&&prime[i]*prime[i]<=kl; i++) {
        
        bool bh=false;
        while (kl%prime[i]==0) {
            kl/=prime[i];
            bh=true;
        }
        if (bh) {
            an=min(an,(x/prime[i]+1)*prime[i]-x);
        }
        if (kl==1) {
            break;
        }
    }
    if (kl>1) {
        an=min(an,(x/kl+1)*kl-x);
    }
    printf("%d\n",an);
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    get_prime(3300);
    while (t--) {
        solv();
    }
    return 0;
}