强人工智能和弱人工智能:
强人工智能:和人脑一样
弱人工智能:不一定和人脑思考方式一样,但是可以达到相同的效果,弱人工智能并不弱
——————————————————————————————————
机器学习能解决的问题:
1.人工智能只能解决有强规律的事情
2.平滑性问题 人工智能不能解决质数识别问题,因为质数本来是没有规律的
3.结果不变性 天气预报-》不变 股票预测-〉可变
特征提取-》数字量化
特征向量就是一个数组
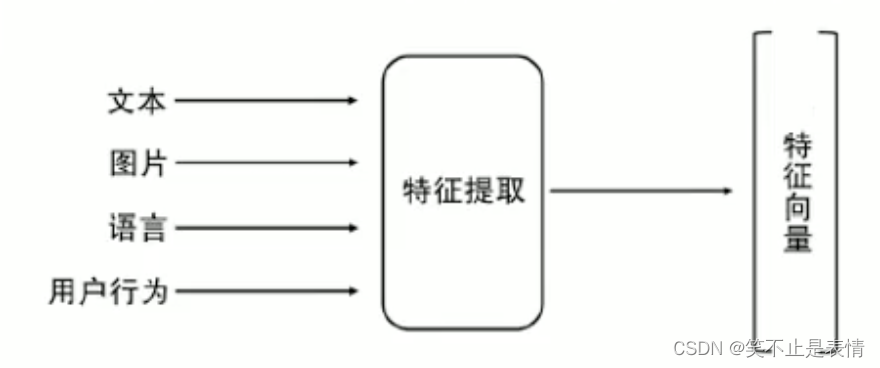
天然向量化:本来就是数字
特征提取时会丢失很多客观事实,是一个信息丢失的过程
图片-》对于一个400400像素的图像-〉特征提取之后4004003(3是RGB的三通道,400400像素的每一个位置都是三维的)
黑白图片-》4004001(1是灰度,范围0~255)
视频-〉多张图片(抽取视频关键帧) 对于机器学习,图片和视频没有本质区别
中文编码:
One-hot编码
常见中文词10w个
我: 【0,1,0,0,……,0,0】
爱: 【0,0,0,1,……,0,0】
中国:【0,0,0,0,……,1,0】
multi-hot编码
我爱中国:【0,1,0,1,……、,1,0】
hot编码的缺点
所有词的差异都是相同的,看不出来词和词之间的差异,语义丢失
丧失循序性
浪费存储时间
hot编码应用场景:性别编码
特征向量化没有绝对的好,向量和需求要契合
微博社交网络,如何表示特征?
人少的时候:邻接矩阵
人多的时候:?
即使同一场景,提取特征也需要看数量级
向量化的好处:可以衡量节点之间的距离
关于距离
——————————————————————————————————
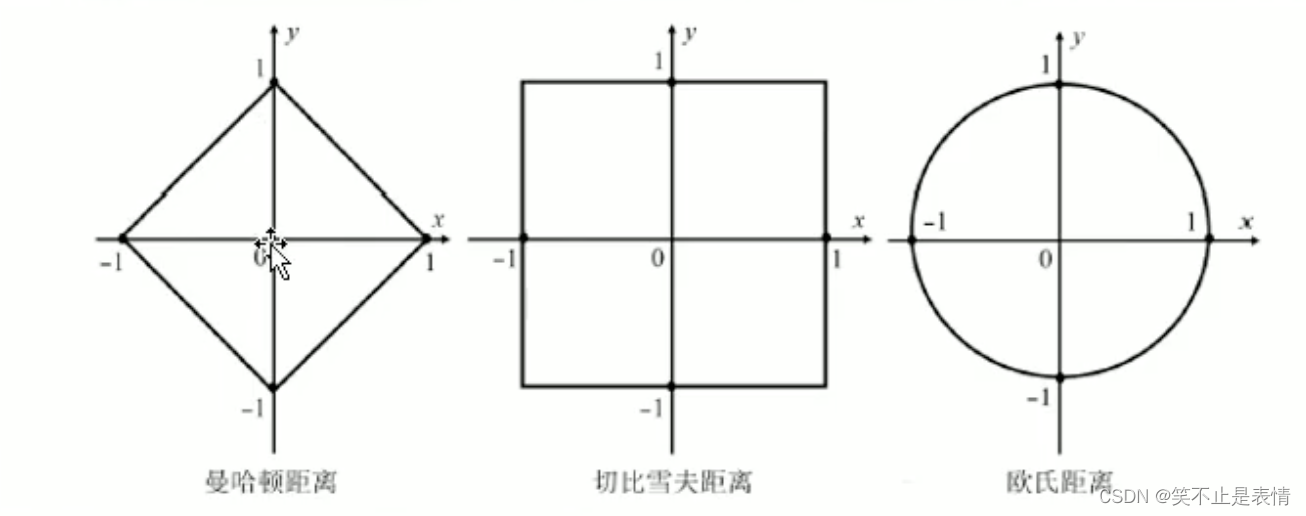
1.欧氏距离:数学中的距离,距离唯一
2.曼哈顿距离:城市街区行走,两地之间的距离,距离不唯一
3.切比雪夫距离:国际象棋国王的行走,向周围8个方向行走的距离都是1,在欧氏距离中是根号2,曼哈顿距离中是2
公式表示为:max(|x1-x2|,|y1-y2|)

在真实产品需求中
对两个产品之间的距离一般计算相似度,并且相似度存在一个值域范围
一般使用公式(1/1+阿尔法)来计算相似度,使得相似度处于区间(0,1】中,并且阿尔法越大,相似度越不敏感
在流形面上,距离会失效,只能找近的,近义词,不能找远的
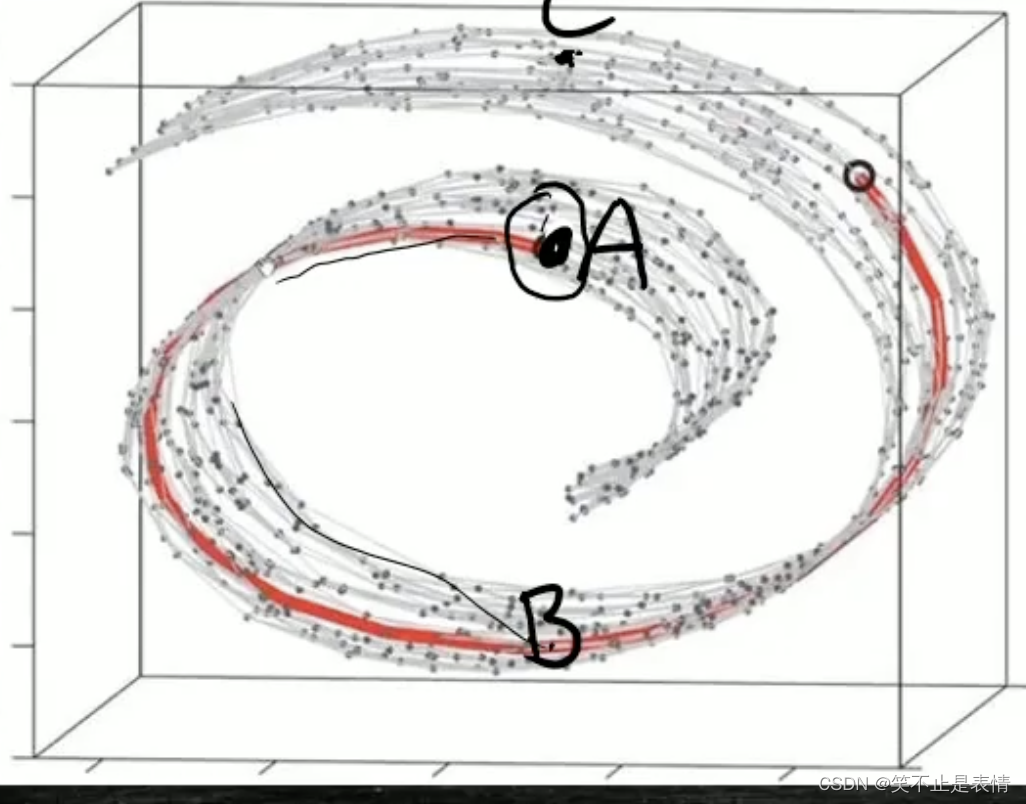
欧式距离的缺点:
身高体重 150cm 40kg
【1.5,40】-》【150,40】- 〉【1500,40】
使用不同单位,对结果影响不一样,例如上述过程中就在逐步放大身高作用
所以需要做归一化
方差和量纲成正比,量纲越大,方差越大