---

欧拉函数

欧拉函数的定义

对于任意正整数 $n$,欧拉函数 $\phi (n)$ 表示小于或等于 $n$ 的正整数中，与 $n$ 互质的正整数个数。

例如:

• $\phi (1)=1$，因为 $1$ 只与 $1$ 互质。
• $\phi (6)=2$，因为与6互质的数有 $1$ 和 $5，共 $2$ 个。
• $\phi (10)=4$，因为与10互质的数有 $1、3、7$ 和 $9$，共 $4$ 个。

欧拉函数的公式

对于任意正整数 $n$，$\phi (n)=n\ast (1-\frac{1}{P_1})\ast (1-\frac{1}{P_2})\ast ...\ast (1-\frac{1}{P_k})$，其中，$P_1,P_2,...,P_k$ 是 $n$ 的不同的质因数。

欧拉函数公式，只与因子相关，与指数无关。

例如:
$\phi (10)=10\ast (1-\frac{1}{2})\ast (1-\frac{1}{5})=4$
$\phi (15)=15\ast (1-\frac{1}{3})\ast (1-\frac{1}{5})=8$

欧拉函数的公式推导

利用容斥原理的推导过程：

对数字N进行质因数分解，可得
$$N=P_1^{r_1}\ast P_2^{r_2}\ast P_3^{r_3}\ast ...\ast P_k^{r_k}$$

由于不能与 $N$ 不互质，所以 $1$ ~ $N$ 不可包含 $P_1,P_2,...,P_k$ 这些质因子。

把 $P_1,P_2,...,P_k$ 的倍数都减去，分别减去 $\frac{N}{P_1},\frac{N}{P_2},...,\frac{N}{P_k}$ 个。

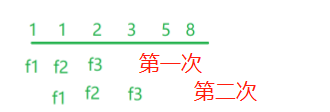
如图所示：

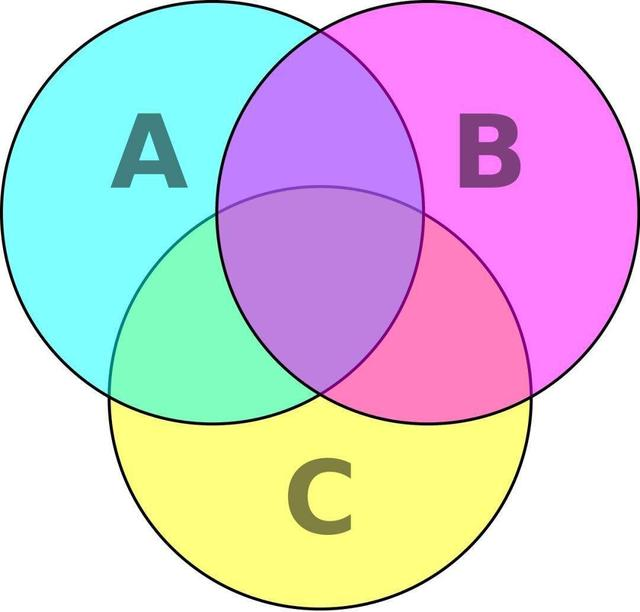
但是由于 $P_1,P_2,...,P_k$ 不同质因子的倍数可能会出现重复，有些数重叠的数会被多次减去。如图中重叠部分会被多次相减，因此要补上重叠的数。比如某个数，是 $P_2$ 的倍数，也是 $P_3$ 的倍数，就减了两回，还需要再加回来 $P_2\ast P_3$ 的倍数，换做是其他的组合就是 $\frac{N}{P_1\ast P_2},\frac{N}{P_1\ast P_{P}3},...,\frac{N}{P_1\ast P_k},..$

但是更多质因子重叠的部分又会弥补至减去之前的状态，得继续减去。如$P_1\ast P_2\ast P_3$这样的更多质因子重叠的部分，而后就像之前一样一减一加最终推出结果。

$$\phi (N)=N\ast (1-\frac{1}{P_1})\ast (1-\frac{1}{P_2})\ast ...\ast (1-\frac{1}{P_k})$$

欧拉定理

如果 $a$ 和 $n$ 是正整数，且 $a$ 与 $n$ 互质,则$$a^{\phi (n)}\equiv 1(\mathrm{mod}n)$$
如果 $n$ 为质数，则$$a^{n-1}\equiv 1(\mathrm{mod}n)$$

典型例题

题目描述：
给定 n 个正整数 ai，请你求出每个数的欧拉函数。

输入格式：
第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式：
输出共 n 行，每行输出一个正整数 ai 的欧拉函数。

数据范围：
$1\le n\le 100,1\le a_i\le 2\times 10^9$

输入样例：

3
3
6
8

输出样例：

2
2
4

代码实现

res对不同的质数只需计算一次，不要将res的计算放到循环中。
res计算过程中要避免出现小数的情况，将除法提前与大数进行。

#define _CRT_NO_SECURE_WARNINGS
#include<iostream>

using namespace std;

int phi(int x)
{
	int res = x;
	for (int i = 2; i <= x / i; ++i)
	{
		if (x % i) continue;
		
		// res对不同的质数只需计算一次，不要将res的计算放到循环中
		res = res / i * (i - 1); // 注意避免出现小数情况

		while (x % i == 0) x /= i;
	}
	if (x > 1) res = res / x * (x - 1);
	return res;
}
int main()
{
	int n;
	cin >> n;
	while (n--)
	{
		int a;
		cin >> a;
		cout << phi(a) << endl;
	}
	return 0;
}

筛法求欧拉函数

思路分析

• 如果这个数是质数，那么对质数 $i$ 的欧拉函数值是 $phi[i]=i-1$。
• 如果 $i$ % $primes[j]==0$，那么 $phi[i\ast primes[j]]=phi[i]\times primes[j]$。（相当于 $i$ 中的质因子包括了 $primes[j]$）
• 如果 $i$ % $primes[j]$ $!=0$，那么 $phi[i\ast primes[j]]=phi[i]\times (primes[j]-1)$。（通过公式变形得来）

经典例题

题目描述：
给定一个正整数 $n$，求 $1$ ~ $n$ 中每个数的欧拉函数之和。

输入格式：
共一行，包含一个整数 $n$。

输出格式：
共一行，包含一个整数，表示 $1$ ~ $n$ 中每个数的欧拉函数之和。

数据范围：
$1<n<10^6$

输入样例：

6

输出样例:

12

代码实现

#define _CRT_NO_SECURE_WARNINGS
#include<iostream>

using namespace std;

const int N = 1e6 + 10;
int phi[N], primes[N], cnt;
bool st[N];
void get_eulers(int n)
{
	for (int i = 2; i <= n; ++i)
	{
		phi[1] = 1;
		if (!st[i])
		{
			phi[i] = i - 1;
			primes[cnt++] = i;
		}
		for (int j = 0; primes[j] <= n / i; ++j)
		{
			st[primes[j] * i] = true;
			if (i % primes[j] == 0)
			{
				phi[primes[j] * i] = phi[i] * primes[j];
				break;
			}
			phi[primes[j] * i] = phi[i] * (primes[j] - 1);
		}
	}
}
int main()
{
	int n, res = 0;
	cin >> n;
	get_eulers(n);
	for (int i = 1; i <= n; ++i) res += phi[i];
	cout << res << endl;
	return 0;
}