0. Simulink模块是什么？能干什么？

Simulink是Matlab软件的框图设计环境，可用于各种动态系统的建模、分析与仿真过程。如：导航制导、通讯、电子、机械、热力学等诸多领域。这些系统在数学角度描述上涉及连续、离散、非线性、时变等用解析方法难以求解的系统，因而采用Simulink进行建模与仿真是指导这些系统分析与设计的一种重要工具。

1. 弹簧阻尼模型简介

1.1 受常力的弹簧阻尼模型

对于一个弹簧阻尼系统，在受到恒力F作用，产生的位移为x，其模型如下图所示，

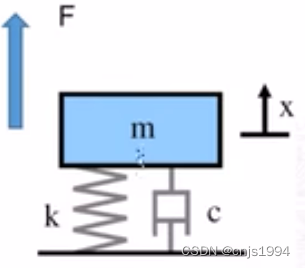
1.2 动力学方程

那么其动力学方程可表示为以下形式：
$$m\ddot{x}+c\dot{x}+kx=F$$
经变换，可表示为如下形式：
$$\ddot{x}=\frac{1}{m}\left(F-c\dot{x}-kx\right)$$

2. simulink模型构建

2.1 Simulink基础模块使用

• 可以观察到，方程中主要包括了x的一阶、二阶导数和x，导数可以使用积分器（integrator）构造，单击界面，输入integrator，单击回车，即可产生该模块，然后对输入、输出进行简单标记。此处，输入为dx（x的一阶导数），输出为x。
  
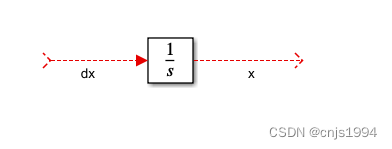
• 同理，可以构造二阶导数的积分器，并连线、注释
  -
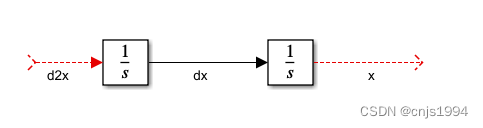
• 同理，可以构造出如下图所示的三个子项$F-c\dot{x}-kx$
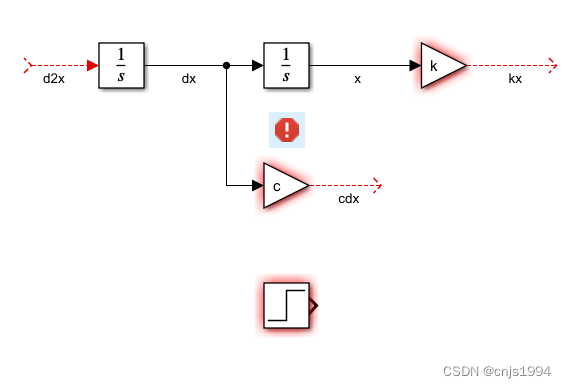
• 最后，用Sum和增益器件（Gain）实现对求和后的项目除以m（乘以1/m），连接其他子回路，得到如下所示：
  

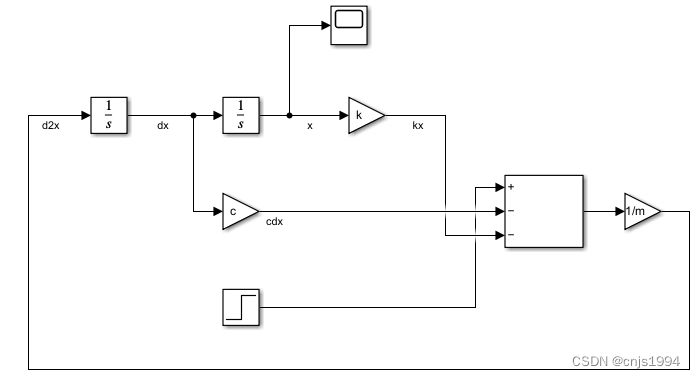
2.2 结果可视化

在matlab的命令行窗口设置F、k、c、m各个常参数的值
此外，可以通过simulink顶端的 建模-模型设置-步长，使得响应曲线更为平滑，仿真结果如下：

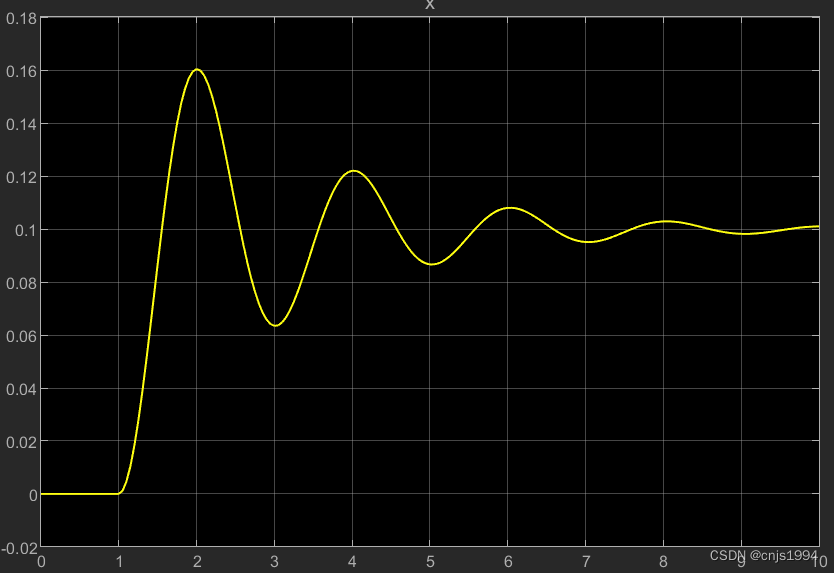
后记

这个系列将持续更新作者对simulink这个模块的学习和心得，欢迎交流与讨论！