有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2
示例 2：

 

 

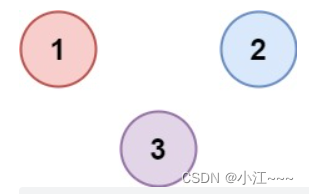
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3
 

提示：

1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] 为 1 或 0
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

解题思路

1. 先判断数组是否为空，空则不必判断是否存在元素了
2. 把所有结点的根至为结点本身
3. 检查结点是否在同一个并查集，没有则把其中一个结点的根设置为另一个结点
   1. 检查两结点是否在同一个并查集中的方法是 不断修改结点值为其父结点，当结点等于父结点时，说明已经遍历到根结点，判断两个结点的根结点是否相同，相同说明两个结点在同一并查集,不同才要合并
4. 用count记录所有结点数，每两个结点合并就减少一个

public int findCircleNum(int[][] isConnected) {
        if (isConnected == null || isConnected.length == 0) {
            return 0;
        }
        int n = isConnected.length;
        UnionFind uf = new UnionFind(n);
        for(int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (isConnected[i][j] == 1) {
                    uf.union(i, j);
                }
            }
        }
        return uf.getCount();
    }
    class UnionFind {
        int root[];
        
        int count;

        UnionFind(int size) {
            root = new int[size];
            count = size;
            for (int i = 0; i < size; i++) {
                root[i] = i;
            }
        }

        int find(int x) {
            while(x!=root[x])
                x=root[x];
                return x;
        }

        void union(int x, int y) {
            int rootX = find(x);
            int rootY = find(y);
            if (rootX != rootY) {
                root[rootY] = rootX;
                count--;
            }
        };

        int getCount() {
            return count;
        }
    }