版本说明

当前版本号[20230802]。

版本	修改说明
20230802	初版

数组

数组理论基础

数组是存放在连续内存空间上的相同类型数据的集合。

数组可以方便的通过下标索引的方式获取到下标下对应的数据。

举一个字符数组的例子，如图所示：

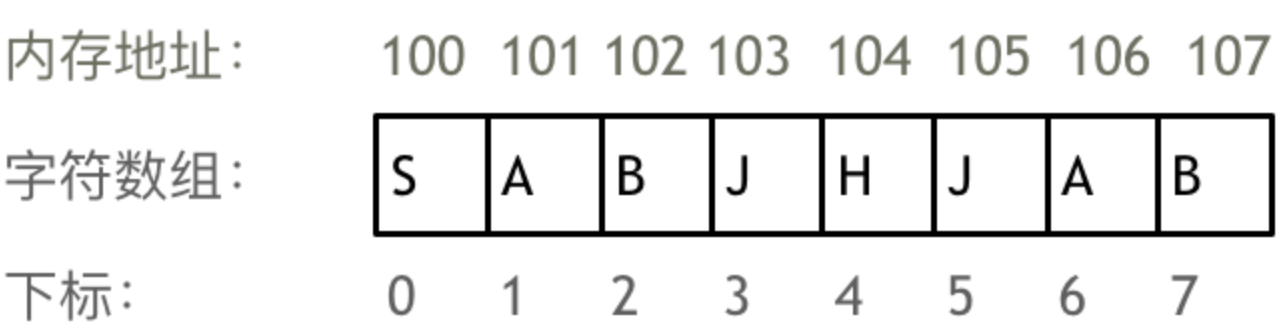
需要两点注意的是

数组下标都是从0开始的。
数组内存空间的地址是连续的

正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

例如删除从左往右数第4个、下标为3的元素，就要对下标为3的元素后面的所有元素都要做移动操作，如图所示：

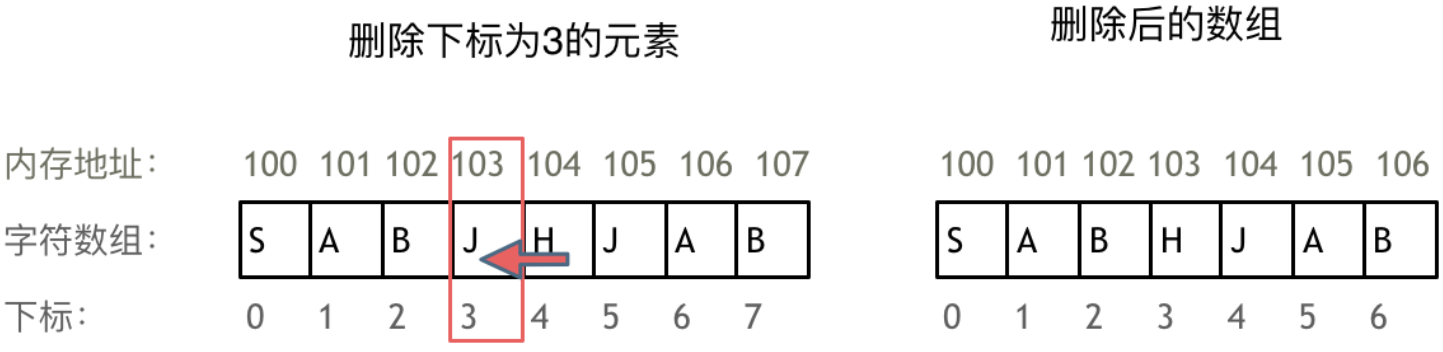
数组的元素是不能删的，只能覆盖。

那么二维数组中，第一个[]代表是行（第一索引），第二个[]代表是列（第二索引）

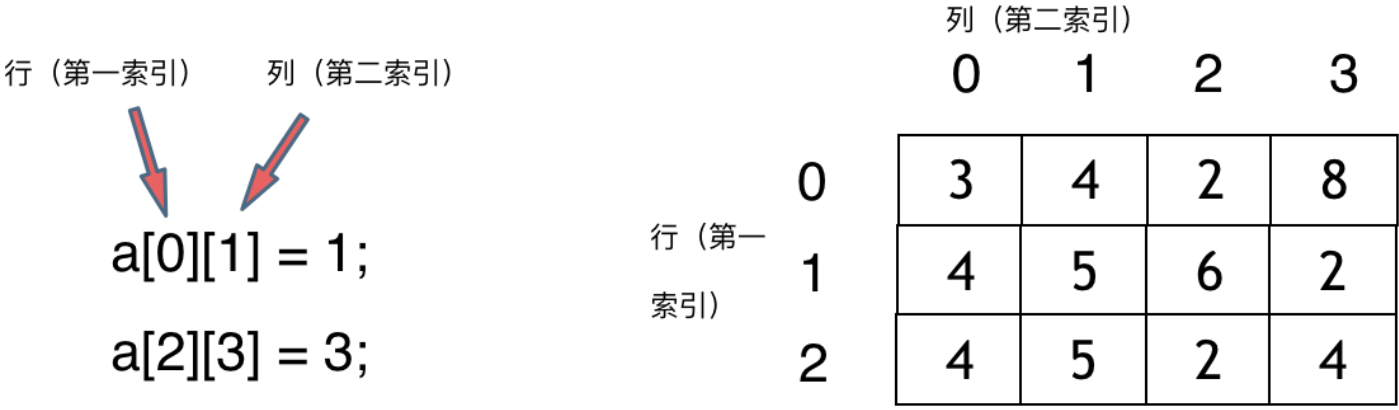
上面的右图中，

b[0][1]    代表的是第0行，第1列      对于图中是数字：4
b[2][0]    代表的是第2行，第0列      对于图中是数字：4

那么二维数组在内存的空间地址是连续的么？

以Java为例，也做一个实验。

package shuzhu;

public class Day01
{
    public static void main(String[] args) {
        int[][] arr = {{1, 2, 3}, {3, 4, 5}, {6, 7, 8}, {9,9,9}};
        System.out.println(arr[0]);
        System.out.println(arr[1]);
        System.out.println(arr[2]);
        System.out.println(arr[3]);
    }
}

所显示：

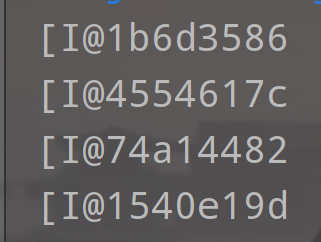
这里的数值也是16进制，这不是真正的地址，而是经过处理过后的数值了，我们也可以看出，二维数组的每一行头结点的地址是没有规则的，更谈不上连续。

所以Java的二维数组可能是如下排列的方式：

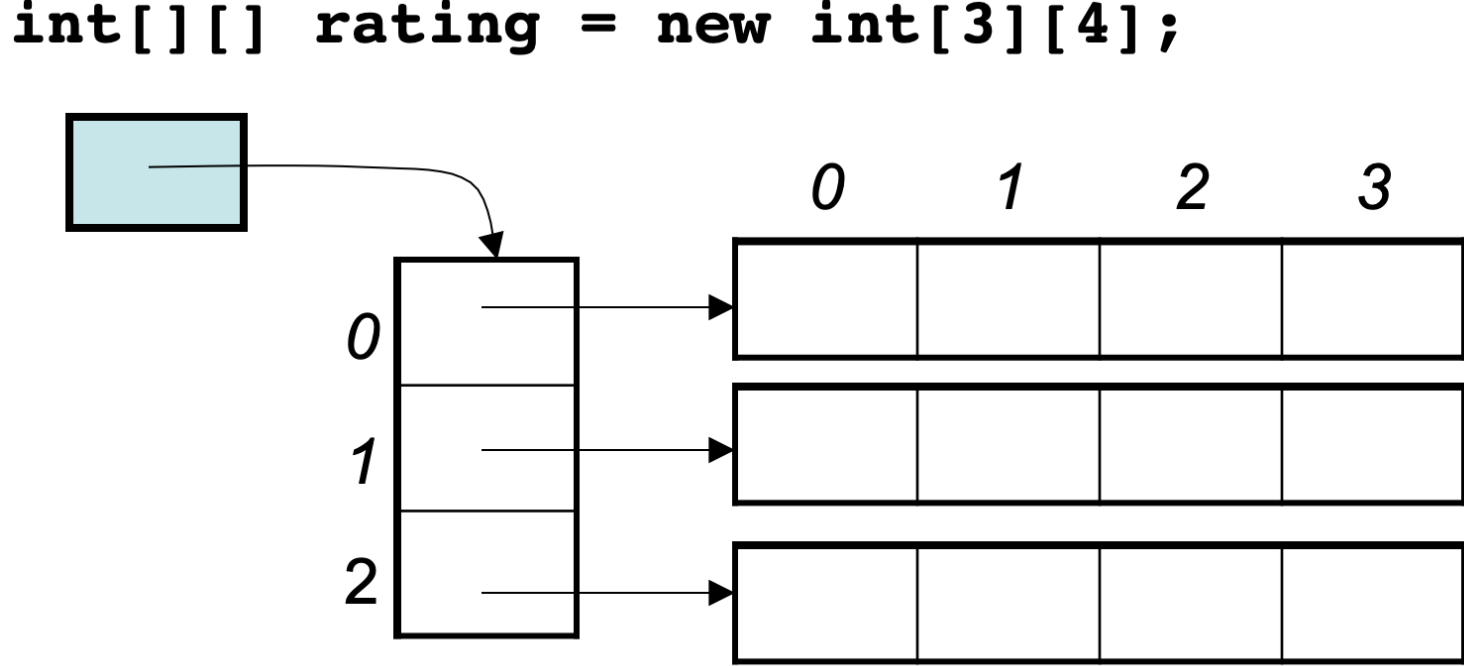
二分查找

力扣题目链接

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9     
输出: 4       
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2     
输出: -1        
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

思路

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

大家写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

下面我用这两种区间的定义分别讲解两种不同的二分写法。

左闭右闭[left, right]

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

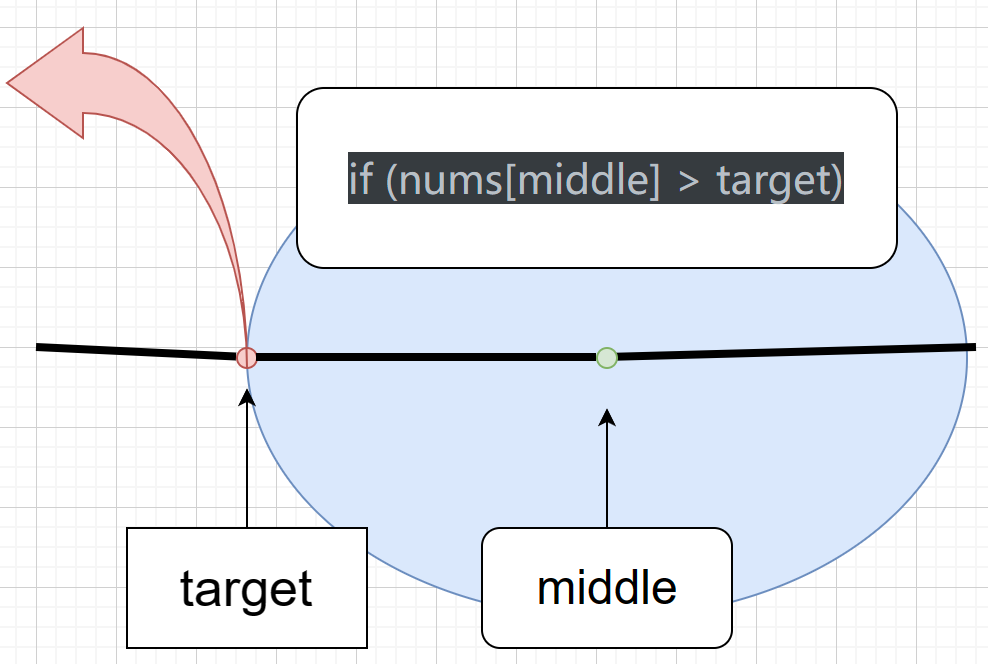
如上图，因为当 if (nums[middle] > target) 时，我们假设middle大于target了，这个范围是在浅蓝色椭圆形区域内，而我们right值取值范围则只能小于这块区域了，只能在橙红色箭头所指左边区域内，因此right可取最大范围为 middle - 1 .

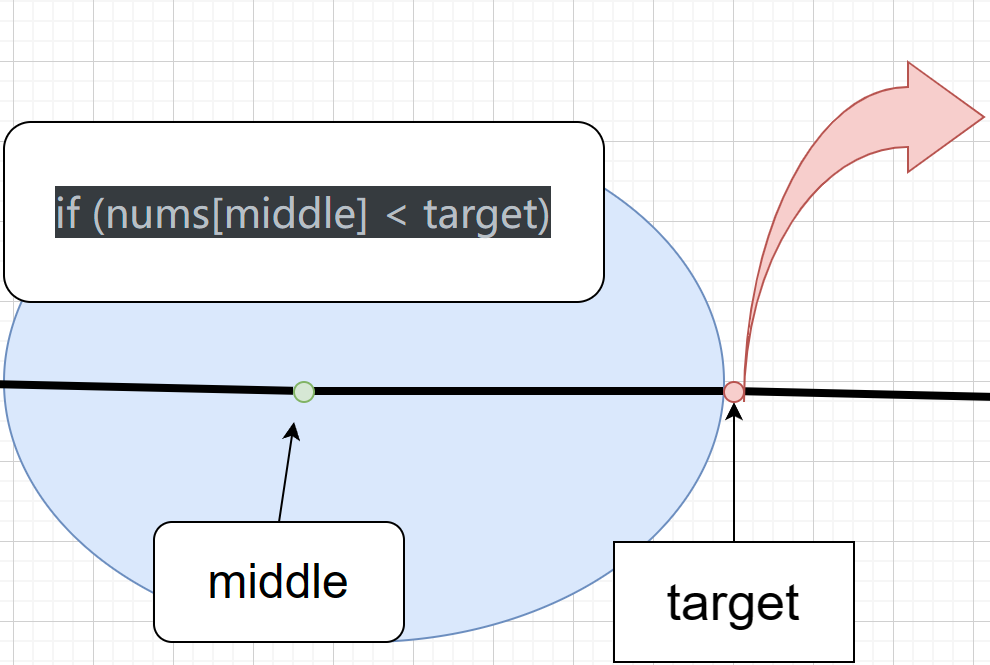
如上图，因为当 if (nums[middle] < target) 时，我们假设middle小于target了，这个范围是在浅蓝色椭圆形区域内，而我们right值取值范围则只能小于这块区域了，只能在橙红色箭头所指左边区域内，因此left可取最小范围为 middle + 1 .

例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：

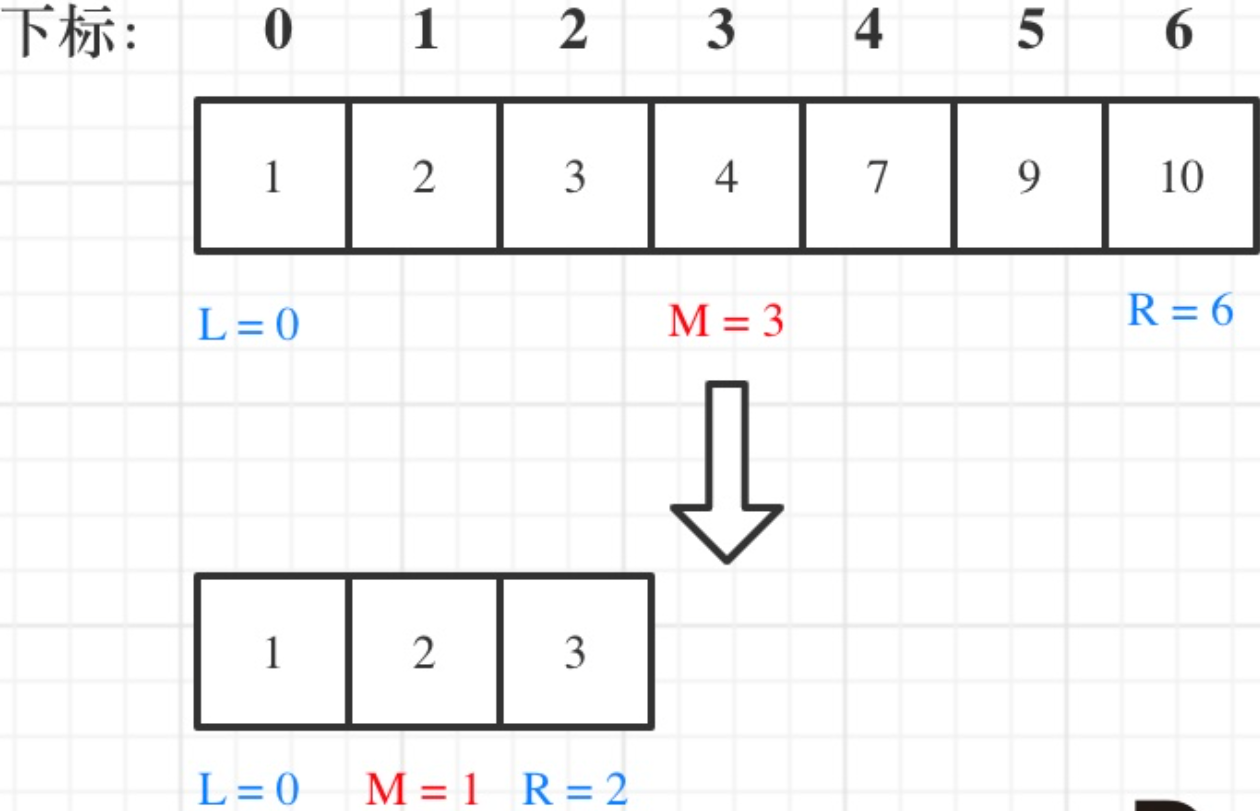
Java示例左闭右闭代码：

public class Day01 {
    public static int search(int[] nums, int target) {
        // 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
        if (target < nums[0] || target > nums[nums.length - 1]) {
            return -1;
        }
        int left = 0, right = nums.length - 1;

        while (left <= right) {
            int mid = left + ((right - left) >> 1);

            // 如果目标值在中间位置，返回下标
            if (nums[mid] == target)
                return mid;

            // 如果目标值比中间位置的数大，增大左边界
            else if (nums[mid] < target)
                left = mid + 1;

            // 如果目标值比中间位置的数小，缩小右边界
            else if (nums[mid] > target)
                right = mid - 1;
        }
        return -1;
    }
}

左闭右开[left, right)

有如下两点：

while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
if (nums[middle] > target) right 更新为 middle，因为**当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，**即：下一个查询区间不会去比较nums[middle]

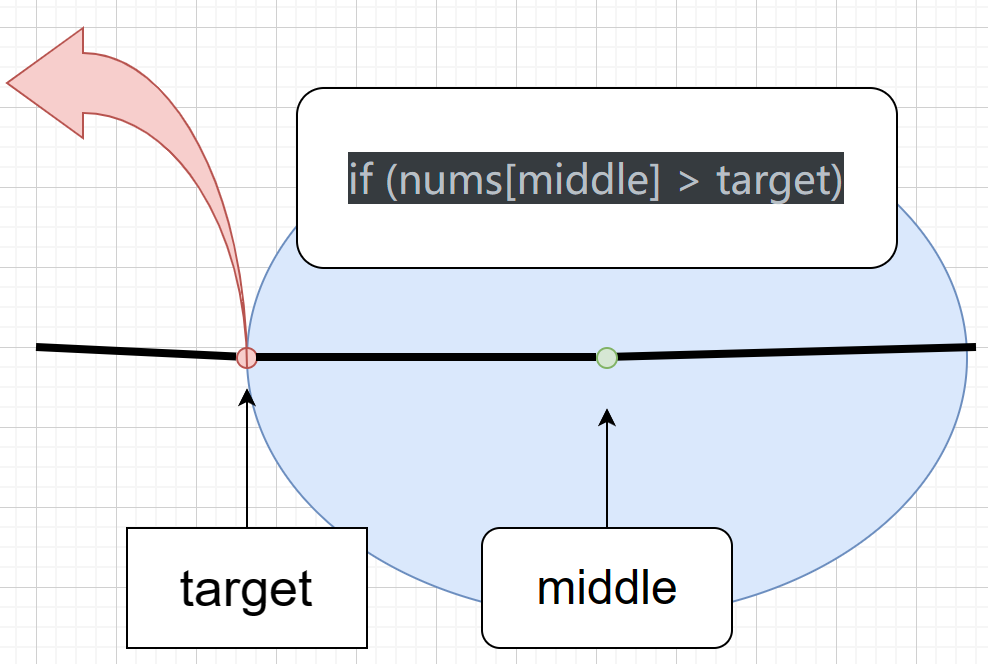
如上图，因为当 if (nums[middle] > target) 时，我们假设middle大于target了，这个范围是在浅蓝色椭圆形区域内，而我们right值取值范围则只能小于这块区域了，只能在橙红色箭头所指左边区域内，但由于我们是左闭右开，本身就取不到right，因此right可取最大范围为 middle .

left 依然等于 middle + 1 .

在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）

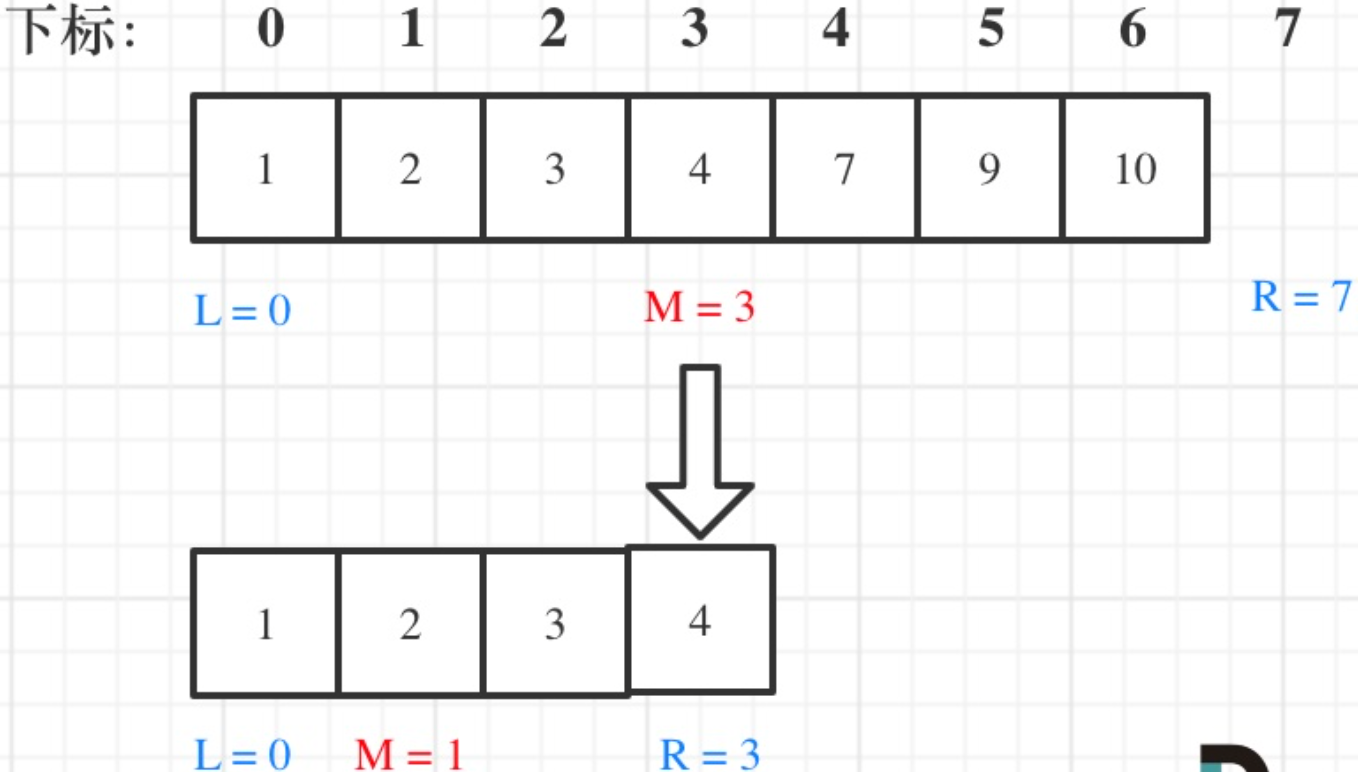
Java示例左闭右开代码：

public class Day01 {
    public static int search(int[] nums, int target) {
        int left = 0, right = nums.length;

        while (left < right) {
            int mid = left + ((right - left) >> 1);

            // 如果目标值在中间位置，返回下标
            if (nums[mid] == target)
                return mid;

            // 如果目标值比中间位置的数大，增大左边界
            else if (nums[mid] < target)
                left = mid + 1;

            // 如果目标值比中间位置的数小，缩小右边界
            else if (nums[mid] > target)
                right = mid;
        }
        return -1;
    }
}

两种方法的区别

左闭右闭方式：
- 【同】定义范围：初始时，左边界left指向数组的第一个元素，右边界right指向数组的最后一个元素。
- 【同】循环终止条件：当left大于right时，表示搜索范围为空，循环终止。
- **【异】**循环体内逻辑：首先计算中间位置mid，然后判断目标值与中间位置的关系，如果目标值小于等于中间位置的值，则将搜索范围缩小到左半部分，即将右边界right更新为mid-1；如果目标值大于中间位置的值，则将搜索范围缩小到右半部分，即将左边界left更新为mid+1。
- 在左闭右闭求法中，将右边界right初始化为nums.length - 1的原因是确保初始的搜索范围包含整个数组。如果右边界初始化为nums.length，那么在初始化时就将右边界设置为超出数组范围的位置，即right = nums.length，这样**在迭代过程中会漏掉最后一个元素。**所以，为了包含整个数组，右边界right的初始值应为nums.length - 1。
- 在给定代码的search方法中，如果目标值小于数组的最小值nums[0]或大于数组的最大值nums[nums.length - 1]，就直接返回-1。这样可以避免进行多余的迭代，提高效率。
左闭右开方式：
- 【同】定义范围：初始时，左边界left指向数组的第一个元素，右边界right指向数组的最后一个元素的下一个位置。
- 【同】循环终止条件：当left等于right时，表示搜索范围为空，循环终止。
- **【异】**循环体内逻辑：首先计算中间位置mid，然后判断目标值与中间位置的关系，如果目标值小于中间位置的值，则将搜索范围缩小到左半部分，即将右边界right更新为mid；如果目标值大于等于中间位置的值，则将搜索范围缩小到右半部分，即将左边界left更新为mid+1。
- 在二分查找题的左闭右开求法中，将右边界right初始化为nums.length的原因是确保初始的搜索范围包含整个数组。如果右边界初始化为nums.length - 1，那么在初始化时就将右边界设置为数组最后一个元素的位置，即right = nums.length - 1，这样**在迭代过程中会漏掉最后一个元素。**所以，为了包含整个数组，右边界right的初始值应为nums.length。
- 在给定代码的search方法中，循环终止条件是left < right，而不是传统的left <= right。这是因为右边界right的定义是开区间，而不是闭区间。当left与right相等时，搜索范围为空，循环终止。
  
  两种方式的不同之处在于循环终止条件的判断和范围的定义方式，但它们都可以实现二分查找的功能。

总结

其实主要就是对区间的定义没有理解清楚，在循环中没有始终坚持根据查找区间的定义来做边界处理。

区间的定义就是不变量，那么在循环中坚持根据查找区间的定义来做边界处理，就是循环不变量规则。

本篇根据两种常见的区间定义，给出了两种二分法的写法，每一个边界为什么这么处理，都根据区间的定义做了详细介绍。

测试代码：

package shuzhu;


public class Day01 {
    public static int search(int[] nums, int target) {
        int left = 0, right = nums.length;

        while (left < right) {
            int mid = left + ((right - left) >> 1);

            // 如果目标值在中间位置，返回下标
            if (nums[mid] == target)
                return mid;

            // 如果目标值比中间位置的数大，增大左边界
            else if (nums[mid] < target)
                left = mid + 1;

            // 如果目标值比中间位置的数小，缩小右边界
            else if (nums[mid] > target)
                right = mid;
        }
        return -1;
    }

    public static void main(String[] args) {
        int[] nums = {1, 3, 5, 7, 9, 11, 13};

        int target = 13;
        int result = search(nums, target);
        if (result == -1) {
            System.out.println("目标值不在数组中。");
        } else {
            System.out.println("目标值在数组中的下标为：" + result);
        }

    }
}