寻找丢失数字：数学与位运算的解密之旅

news2024/10/6 5:57:31

在这里插入图片描述

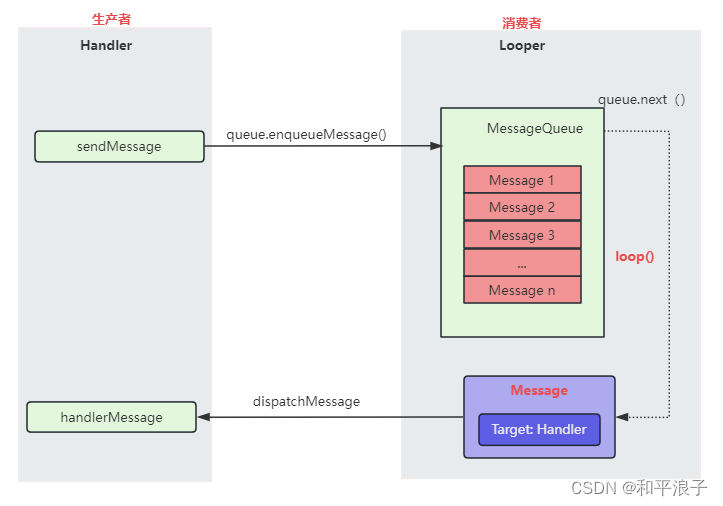
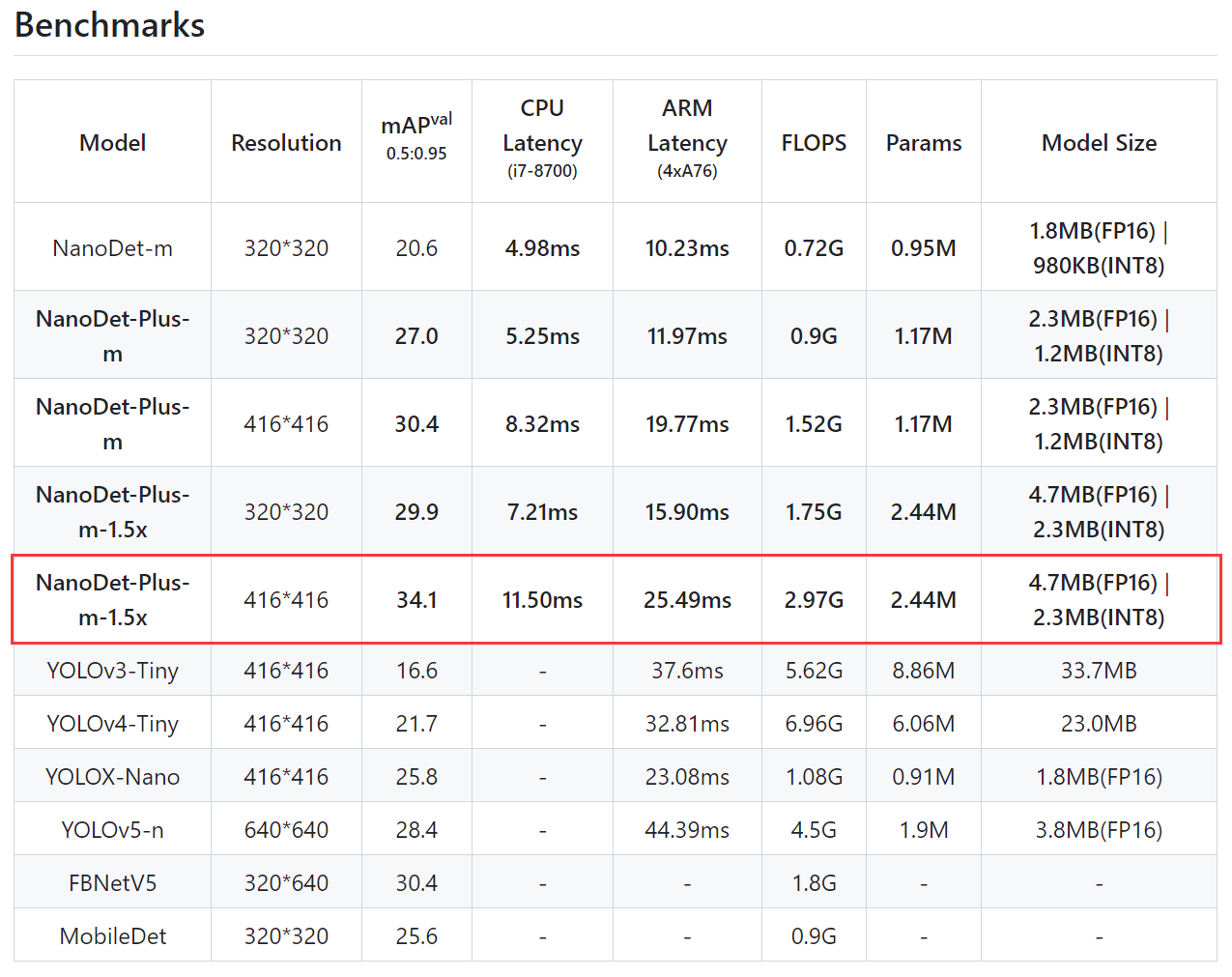
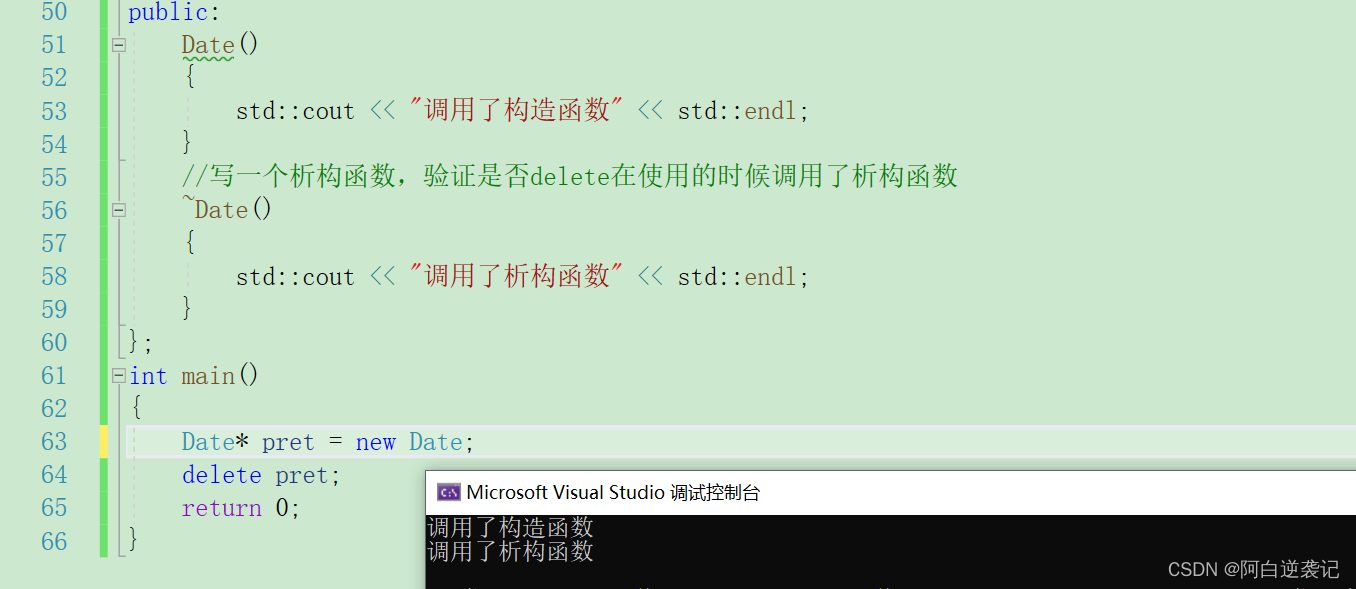
本篇博客会讲解力扣“268. 丢失的数字”的解题思路，这是题目链接。

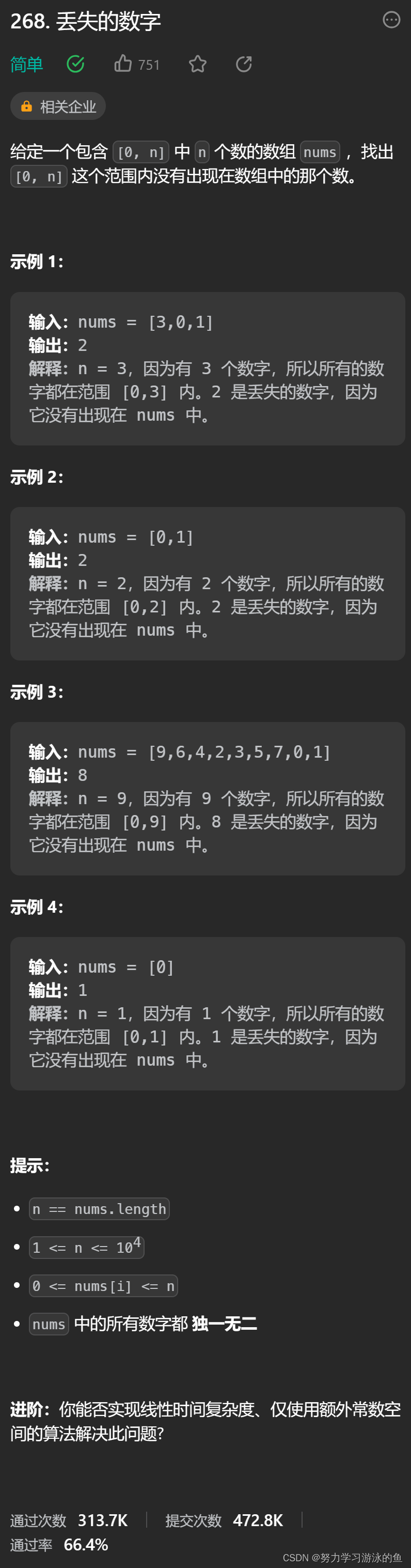
在这里插入图片描述
注意进阶中的描述：你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题？这里我会讲解两种思路，它们的时间复杂度是O(N)，空间复杂度是O(1)。

思路一：数学

本题可以使用数学的方法求解。我们先使用等差数列求和公式，计算0+1+2+…+n的值，再减去数组中的所有值，得到的就是丢失的数字。

int missingNumber(int* nums, int numsSize) {
	// 求和0+1+2+...+n
	int ret = (1 + numsSize) * numsSize / 2;

	// 减去数组中的数
	for (int i = 0; i < numsSize; ++i)
	{
		ret -= nums[i];
	}

	return ret;
}

在这里插入图片描述

思路二：位运算

我们也可以使用位运算来解决这道题目。我们先创建一个变量并初始化成0，接着把0到n的数字都和这个变量异或，最后把数组中的数字都和这个变量异或，就能得到丢失的数字。这是因为异或运算具有交换律、结合律，且相同数字异或的结果是0，任何数字和0异或的结果都是这个数字本身，所以0到n中除了丢失的数字之外，异或后都抵消掉了，只留下丢失的数字。

int missingNumber(int* nums, int numsSize){
    // 计算0^1^2^...^n
    int ret = 0;
    for (int i = 1; i <= numsSize; ++i)
    {
        ret ^= i;
    }

    // 异或数组中的数据
    for (int i = 0; i < numsSize; ++i)
    {
        ret ^= nums[i];
    }

    return ret;
}