本节中我们考虑一个更为复杂的常微分方程模型，
$$\begin{gathered} \frac{d{X}_C}{dt}=\nu (X_A+Y_A)-\beta \cdot X_C\cdot (Y_C+Y_A)-(\mu +g)\cdot X_C,(1) \\ \frac{d{Y}_C}{dt}=\beta \cdot X_C\cdot (Y_C+Y_A)-(\mu +g+\rho )\cdot Y_C,(2) \\ \frac{d{X}_A}{dt}=g\cdot X_C-\beta \cdot X_A\cdot (Y_C+Y_A),(3) \\ \frac{d{Y}_A}{dt}=\beta \cdot X_A\ast (Y_C+Y_A)+g\ast Y_C-\rho \ast Y_A(4) \end{gathered}$$
该常微分方程系统用于模拟一种树木传染病动态，其中$X_C$代表易感树苗（susceptible sapling）的个体数，$Y_C$代表感病树苗（infected sapling）的个体数，$X_A$代表易感成年树木的个体数（susceptible adult），$Y_A$代表感病成年树木（infected adult）的个体数。显然$X_C,Y_C,X_A,Y_A\ge 0$。

$(1)$式中，$\nu (X_A+Y_A)$代表繁殖产生新树苗的速率，其中$\nu$是繁殖速率。$-\beta \cdot X_C\cdot (Y_C+Y_A)$指的是由于疾病传染，导致易感树苗转化为感病树苗的速率，其中$\beta$为传染率。$-(\mu +g)\cdot X_C,$是指由于自然死亡及树木成长，导致易感树苗被移除，或是进入到易感成年树木的速率，其中$\mu$为自然死亡率，$g$为树木生长率。

$(2)$式中，$\beta \cdot X_C\cdot (Y_C+Y_A)$代表由易感树苗被传染而转化为感病树苗的速率，$-(\mu +g+\rho )\cdot Y_C$则包含自然死亡、树木成长、因疾病感染而死亡这三个过程，其中$\rho$代表由于传染病而导致的死亡率。

$(3)$式中，$g\cdot X_C$代表由于树木生长而使易感树苗转换为易感成年树木的速率，$-\beta \cdot X_A\cdot (Y_C+Y_A)$代表由于疾病传染，使易感成年大树转换为感病成年大树的速率。

$(4)$式中，$\beta \cdot X_A\ast (Y_C+Y_A)$对应于疾病传染过程，$g\ast Y_C$对应于树木生长过程，$-\rho \ast Y_A$对应于疾病导致的死亡过程。

研究一个常微分方程系统，最为直接的方法是研究其相速矢量场（phase velocity vector filed）。下面我们回顾一下与相速矢量场相关的几个重要概念，

常微分方程中的几个重要概念
相空间（phase space）：是指所有模型变量的所有可能取值的组合构成的空间。在本节案例中，相空间为$\{(X_C,Y_C,X_A,Y_A)|X_C,Y_C,X_A,Y_A\ge 0\}$。
相点（phase point）：相空间中的任意一个点称为相点。相点用于描述系统的状态。在本节案例中，相点$(X_C,Y_C,X_A,Y_A)=(10,60,20,100)$代表系统中有10棵易感树苗、60棵感病树苗、20棵易感成树、100棵感病成树。
相速矢量（phase velocity vector）：系统位于某一相点时，其速度大小和方向构成的矢量，叫做该相点所对应的相速矢量。在本节案例中，针对相点$(X_C,Y_C,X_A,Y_A)=(10,60,20,100)$，将$X_C,Y_C,X_A,Y_A$的值代入式$(1-4)$，求出$(\frac{d{X}_C}{dt},\frac{d{Y}_C}{dt},\frac{d{X}_A}{dt},\frac{d{Y}_A}{dt})$，其值便是该相点所对应的相速矢量。相速矢量描述了系统位于某一相点时的运动方向和快慢。
相速矢量场（phase velocity vector field）：相空间中所有相速矢量组成的集合。
相位曲线（phase curve）：相点沿相速矢量场移动所形成的运动轨迹。

在ecode包中，当函数plot作用于eode类的对象时，plot函数会自动绘制出某个常微分方程系统的相速矢量场，或相速矢量。在上一节中，我们介绍了当常微分方程系统中含有两个模型变量时，plot函数的用法。

本节所关注的模型含有四个模型变量$X_C,Y_C,X_A,Y_A$，因而将介绍含有多个模型变量时，plot函数的行为。

一、绘制相速矢量场

首先我们在ecode包中构建上述模型（式$(1-4)$）：

library(ecode)

dX_Cdt <- function(X_C, Y_C, X_A, Y_A, nu = 0.15, beta = 0.1, mu = 0.15, g = 0.04)
  nu * (X_A + Y_A) - beta * X_C * (Y_C + Y_A) - (mu + g) * X_C

dY_Cdt <- function(X_C, Y_C, Y_A, beta = 0.1, mu = 0.15, g = 0.04, rho = 0.2)
  beta * X_C * (Y_C + Y_A) - (mu + g + rho) * Y_C

dX_Adt <- function(X_C, Y_C, X_A, Y_A, beta = 0.1, g = 0.04)
  g * X_C - beta * X_A * (Y_C + Y_A)

dY_Adt <- function(X_A, Y_C, Y_A, beta = 0.1, g = 0.04, rho = 0.2)
  beta * X_A * (Y_C + Y_A) + g * Y_C - rho * Y_A

x <- eode(dX_Cdt = dX_Cdt, dY_Cdt = dY_Cdt, dX_Adt = dX_Adt, dY_Adt = dY_Adt)
x
### An ODE system: 4 equations
### equations:
###   dX_Cdt = nu * (X_A + Y_A) - beta * X_C * (Y_C + Y_A) - (mu + g) * X_C 
###   dY_Cdt = beta * X_C * (Y_C + Y_A) - (mu + g + rho) * Y_C 
###   dX_Adt = g * X_C - beta * X_A * (Y_C + Y_A) 
###   dY_Adt = beta * X_A * (Y_C + Y_A) + g * Y_C - rho * Y_A 
### variables: X_C Y_C X_A Y_A 
### parameters: nu = 0.15, beta = 0.1, mu = 0.15, g = 0.04, rho = 0.2 
### constraints: X_A<1000 X_A>0 X_C<1000 X_C>0 Y_A<1000 Y_A>0 Y_C<1000 Y_C>0

由于我们没有在模型中指定模型变量的范围，ecode包自动将变量范围设置在$(0,1000)$内。此时调用plot函数，

plot(x)
### Set X_A = 500, Y_A = 500 for mapping in two axis

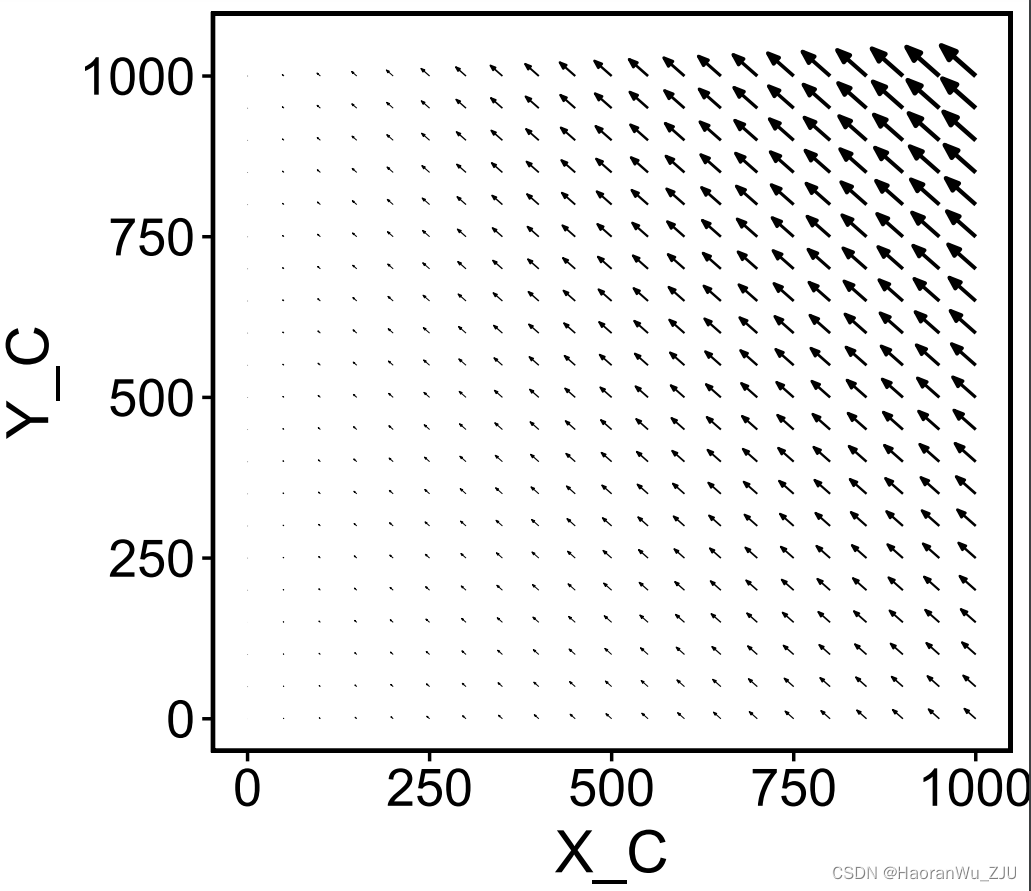
输出结果如图所示。plot函数自动限制了$X_A=500,Y_A=500$，并以$X_C,Y_C$为横、纵坐标系绘制相速矢量场。需要注意的是，该相速矢量图仅仅表示$X_A,Y_A$为固定值时的相速矢量场，该矢量场位于相空间内部的一个平面。

当常微分方程组含有多个模型变量时，如果不给plot任何参数，则plot函数默认会以常微分方程中前两个变量为坐标轴绘制相速矢量场，而其余变量将会被赋上一个固定值，其值等于该模型变量范围的中值。

二、自定义模型变量的值

如果不希望以$X_A=500,Y_A=500$为限制条件，则可以在plot函数中添加set_covar参数，

plot(x, set_covar = list(X_A = 10, Y_A = 20))

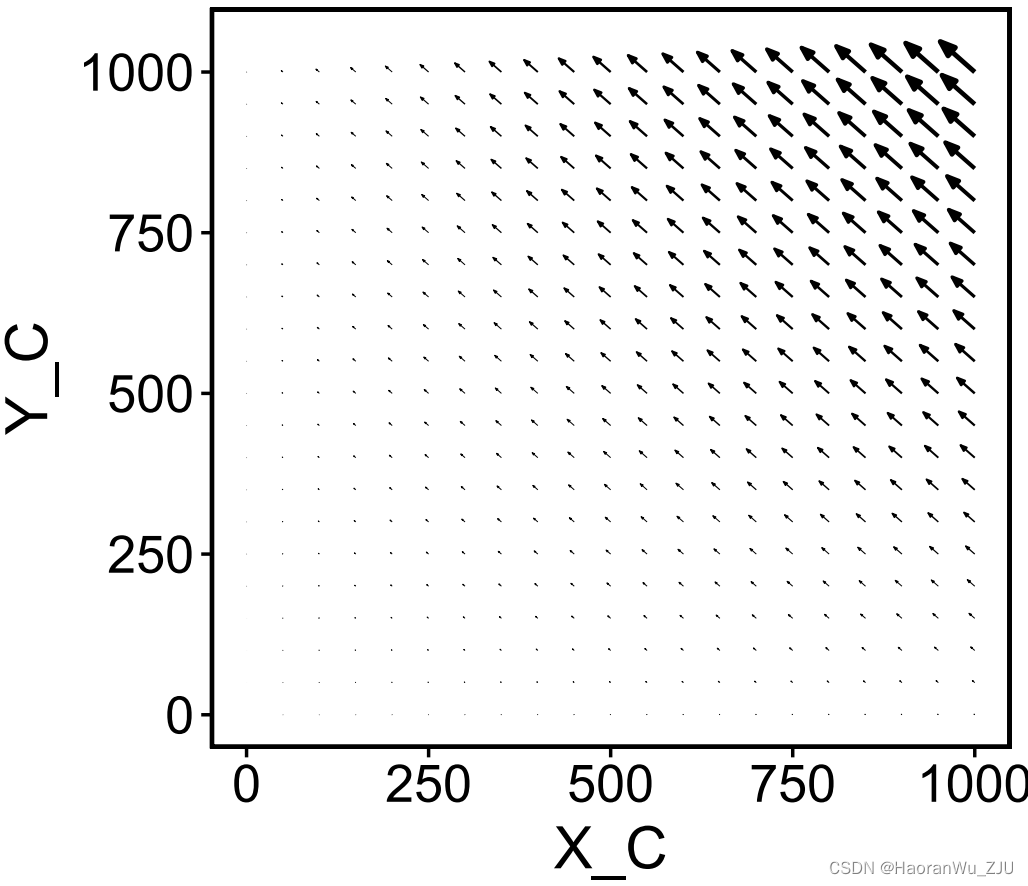此时，plot函数给出的是$X_A=10,Y_A=20$株时，以$X_C,Y_C$为坐标轴作出的相速矢量场。

如果想要固定$X_C,Y_C$，以$X_A,Y_A$为坐标轴作相速矢量场，则

plot(x, set_covar = list(X_C = 10, Y_C = 20))

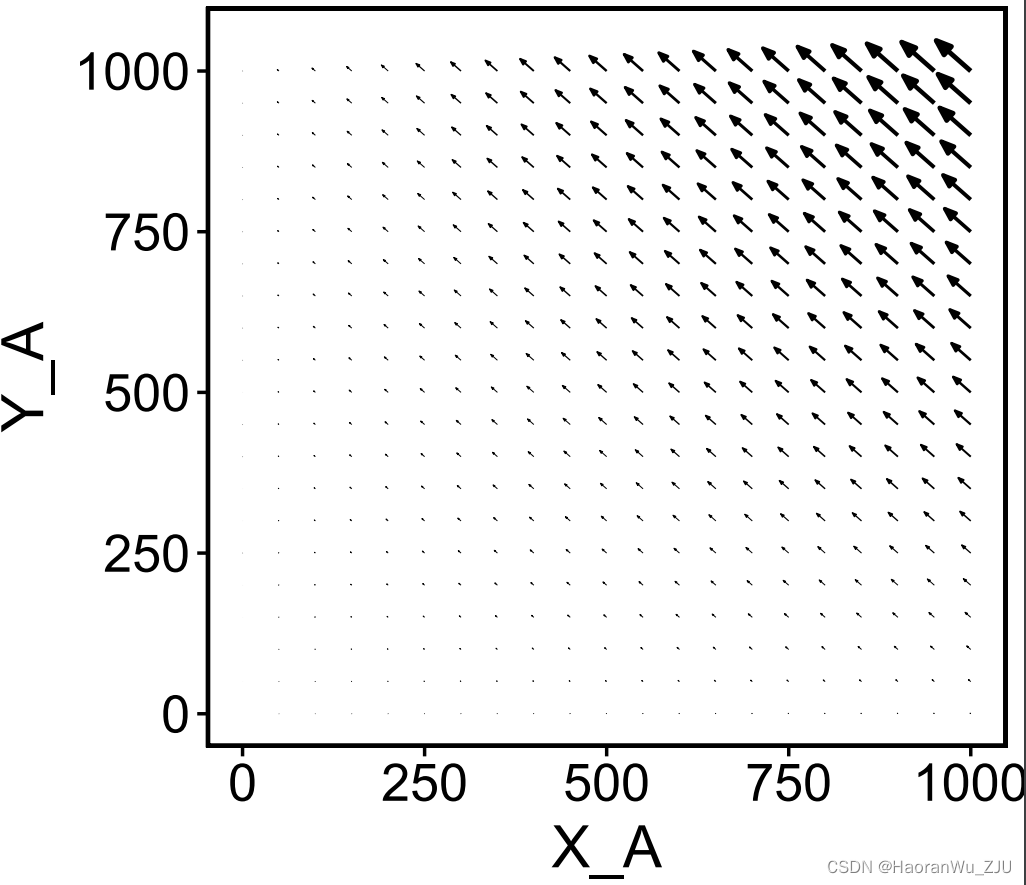
此为$X_C=10,Y_C=20$时，以$X_A,Y_A$为坐标轴的相速矢量场。

三、自定义模型变量的范围

上一节中已经提到，可以采用eode_set_constraint重新设置模型变量的范围。例如，以下代码将$X_C,Y_C,X_A,Y_A$的范围位置为$(0,5)$，

x <- eode_set_constraint(x, new_constraint = c("X_C<5","Y_C<5","X_A<5","Y_A<5"))
x
### An ODE system: 4 equations
### equations:
###   dX_Cdt = nu * (X_A + Y_A) - beta * X_C * (Y_C + Y_A) - (mu + g) * X_C 
###   dY_Cdt = beta * X_C * (Y_C + Y_A) - (mu + g + rho) * Y_C 
###   dX_Adt = g * X_C - beta * X_A * (Y_C + Y_A) 
###   dY_Adt = beta * X_A * (Y_C + Y_A) + g * Y_C - rho * Y_A 
### variables: X_C Y_C X_A Y_A 
### parameters: nu = 0.15, beta = 0.1, mu = 0.15, g = 0.04, rho = 0.2 
### constraints: X_A<5 X_A>0 X_C<5 X_C>0 Y_A<5 Y_A>0 Y_C<5 Y_C>0

接下来，我们尝试固定$X_A=2,Y_A=2$，以$X_C,Y_C$为坐标轴，绘制相速矢量场，

plot(x, set_covar = list(X_A = 2, Y_A = 2))

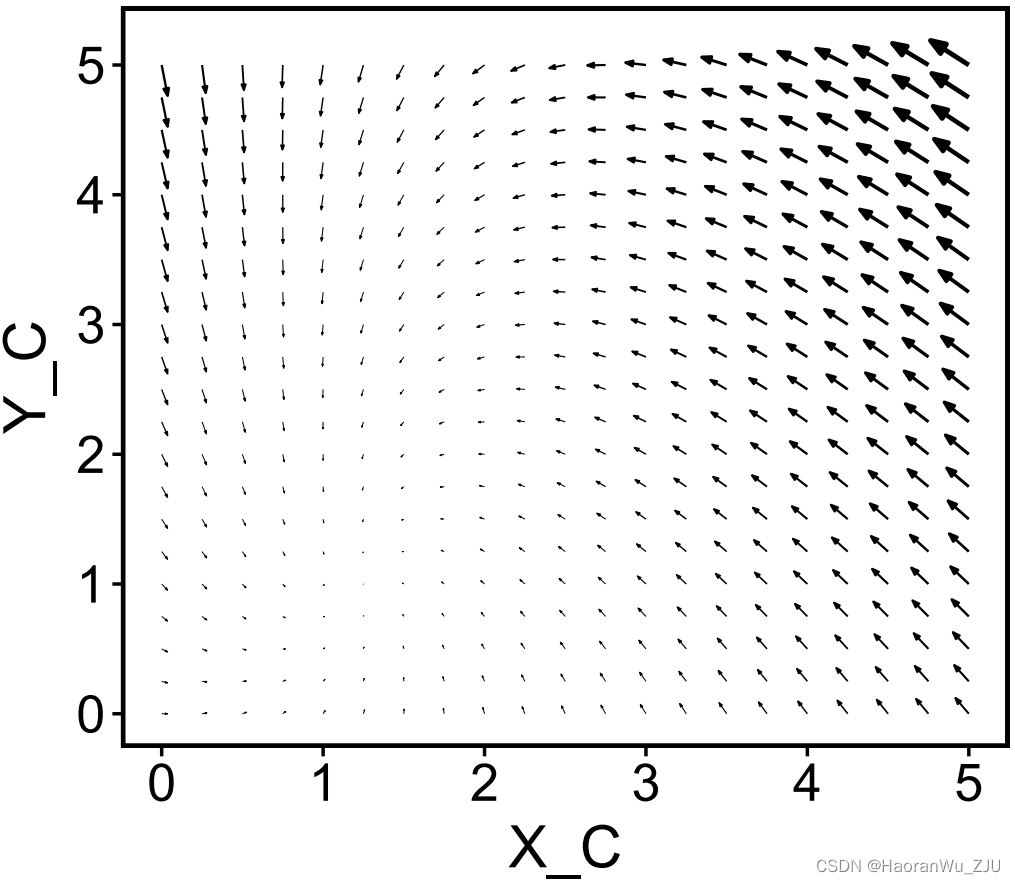
可以看到，该常微分方程组似乎在$X_C,Y_C$的值很小时存在使$d{X}_C/dt,d{Y}_C/dt=0$的点。

四、一维相速矢量场

如果一个常微分方程只有一个模型变量，或者在含有$n$个模型变量的常微分方程组中，有$(n-1)$个变量的值都被固定了，那么plot函数就会绘制一维的相速矢量场。

现在我们尝试固定$X_A=2,Y_A=2,X_C=2$。这样，只剩下模型变量$X_A$的值没有被固定。plot函数将以$X_A$为唯一的坐标轴，绘制一维的相速矢量场，

plot(x, set_covar = list(X_A = 2, Y_A = 2, X_C = 2))

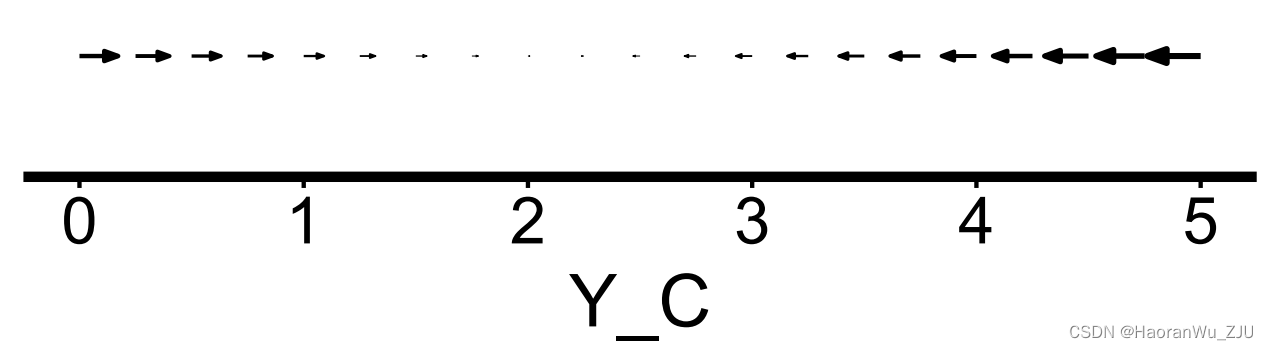
其中，每个相速矢量的值代表的是$d{Y}_C/dt$在某一相点的对应值。

五、相速矢量

当所有模型变量都被赋值时，plot函数将会作出某一相点所对应的相速矢量。在相空间中，相速矢量的起点在其对应的相点，长度代表相点在相点在该处运动的速率。例如，在本节案例中，位于相点$(X_{C0},Y_{C0},X_{A0},Y_{A0})$的相速矢量的值为，
$$(d{X}_C/dt,d{Y}_A/dt,d{X}_A/dt,d{Y}_A/dt){|}_{X_C=X_{C0},Y_C=Y_{C0},X_A=X_{A0},Y_A=Y_{A0}}$$
调用plot时，plot函数会画出相速矢量在各个维度上的值，

plot(x, set_covar = list(X_A = 2, Y_A = 2, X_C = 2, Y_C = 2))

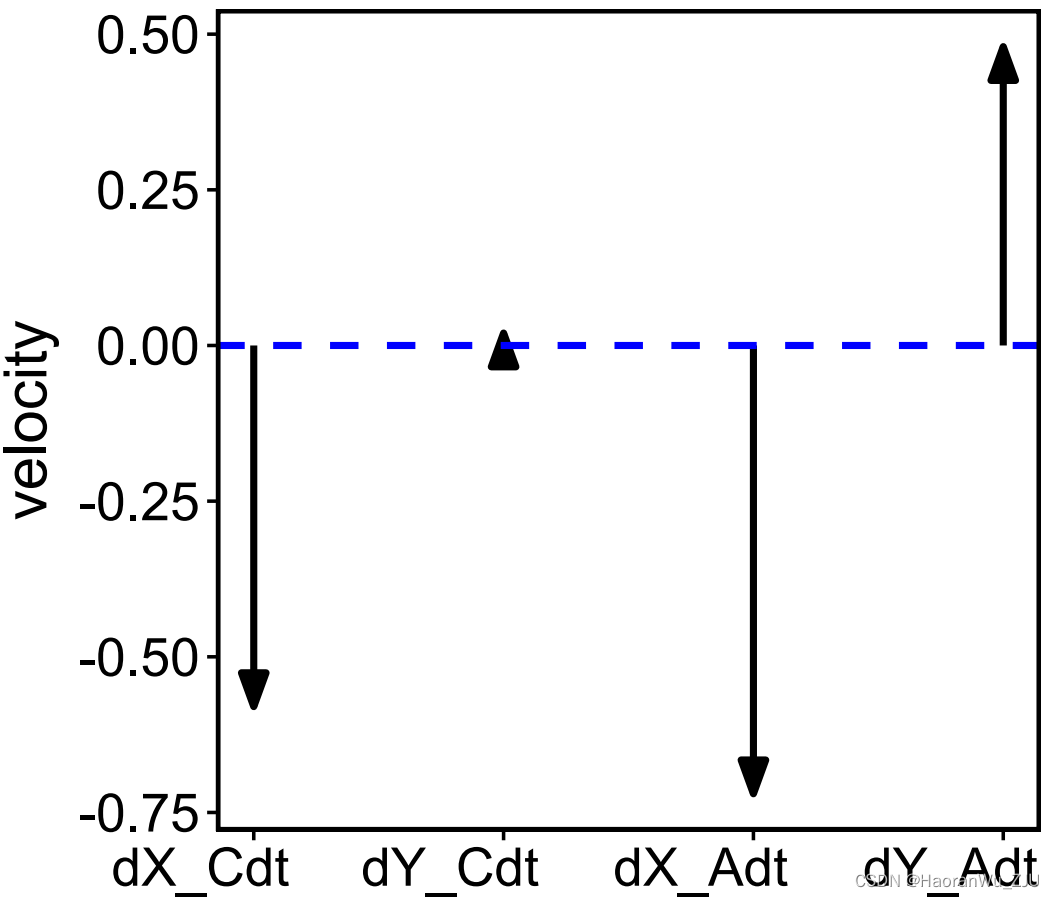
该图给出了相点$(2,2,2,2)$所对应的相速矢量，其中横坐标的每一个标签代表相速矢量在某一维度上的分解值，即$d{X}_C/dt{|}_{X_C=2},d{Y}_C/dt{|}_{Y_C=2},d{X}_A/dt{|}_{X_A=2},d{Y}_A/dt{|}_{Y_A=2}$。

如何引用

Wu, H. (2023). ecode: An R package to investigate community dynamics in ordinary differential equation systems. bioRxiv, 2023-06.

原文见bioRxiv。