代码随想录刷题记录day40 爬楼梯+零钱兑换+完全平方数

参考：代码随想录

70. 爬楼梯

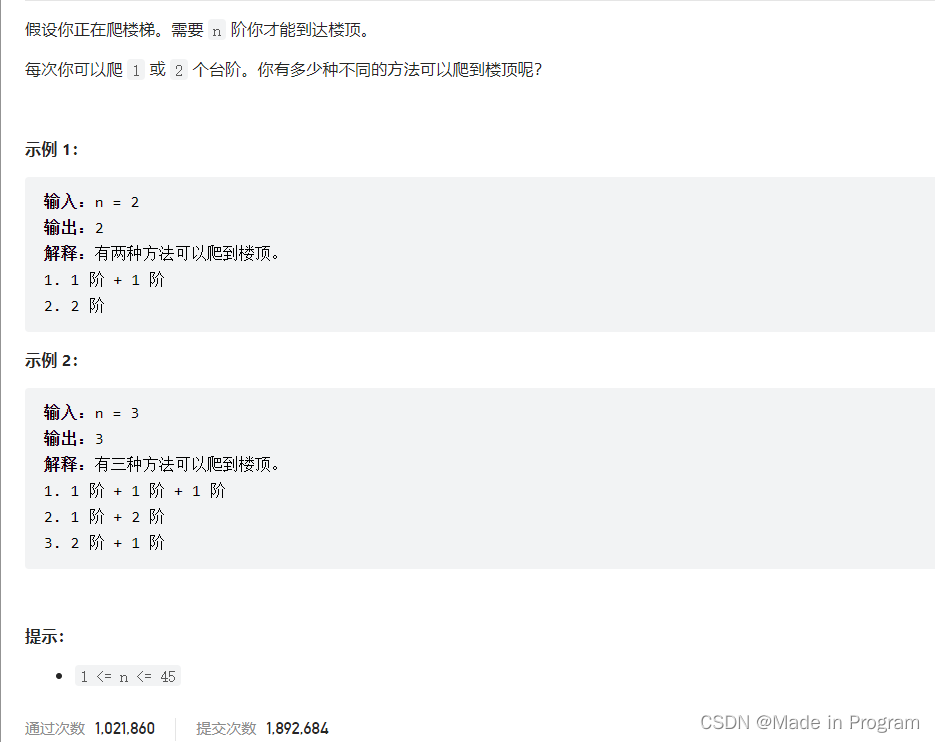
思想

当作完全背包问题，物品是1，2，可以无限次取用，背包的容量是n

1.dp[j]表示容量为j的背包，装满有dp[j]次

2.dp[j]+=dp[j-i]

3.dp[0]=0;

4.遍历顺序 由于是排列问题，所以先便利背包再遍历物品

class Solution {
    // public int climbStairs(int n) {
    //     //动态规划

    //     //dp[i] 表示爬上i个台阶有dp【i】种方法
    //     //dp[i]=dp[i-1]+dp[i-2];
        
    //     int [] dp=new int[n+1];
    //     dp[1]=1;
    //     if(n==1) return 1;
    //     dp[2]=2;

    //     for(int i=3;i<=n;i++){
    //         dp[i]=dp[i-1]+dp[i-2];
    //     }
    //     return dp[n];
    // }
    public int climbStairs(int n) {
        //完全背包问题
        //dp[j]表示装满容量为j的背包 有dp[j]种方法。j就表示台阶的高度
        //物品只有1和2

        int[] dp=new int[n+1];
        // dp[1]=1;
        dp[0]=1;

        for(int j=1;j<=n;j++){//排列问题要先遍历背包
            for(int i=1;i<=2;i++){
                if(j>=i)dp[j]+=dp[j-i];
            }
        }
        return dp[n];

    }
}

322. 零钱兑换

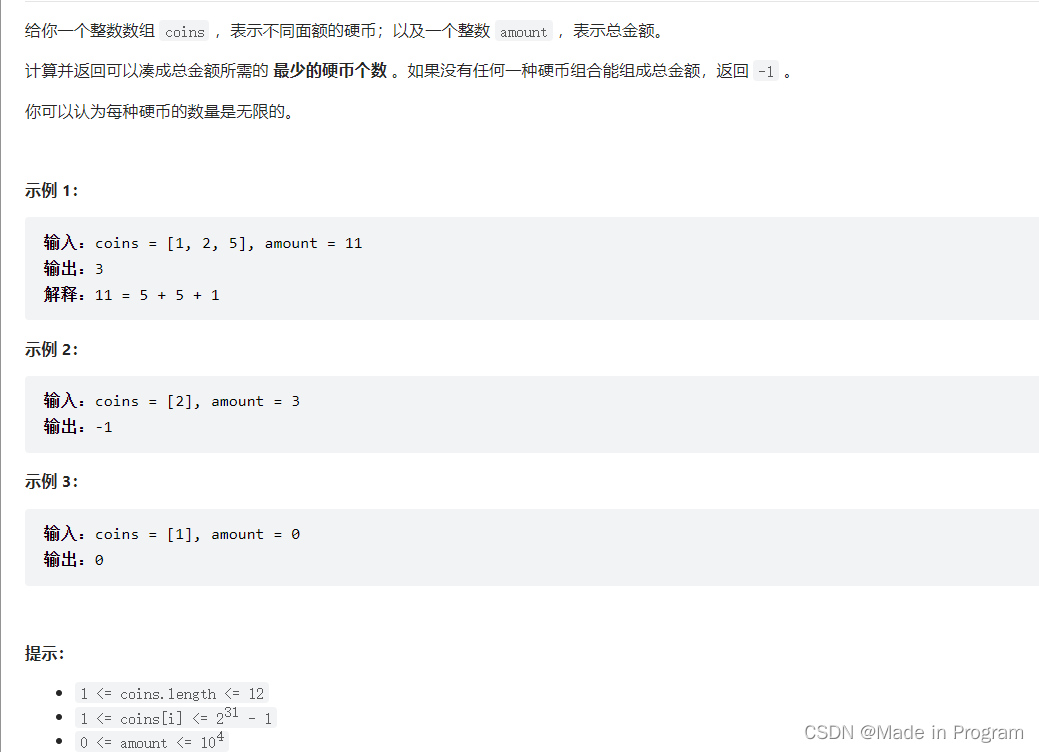
思想

完全背包问题，集合的数据可重复。

1.dp[j]表示容量为j的背包，装满后的最少的物品数是dp[j]

2.dp[j]=Math.min(dp[j], dp[j-coins[i]+1])

3.初始化

dp[0]=0;
for(int i=1;i<=amount;i++){
dp[i]=Integer.MAX_VALUE;
}

4.遍历顺序：

先遍历物品再遍历背包，或者先遍历背包再遍历物品都是可以的。因为求的是一个最小的

if(dp[j-coins[i]]!=Integer.MAX_VALUE) 表示有些背包的容量是无法被装满的，需要过滤

代码

class Solution {
    public int coinChange(int[] coins, int amount) {
        //之前的题目 完全背包
        //dp[j]表示容量为j的背包，装满有dp[j]种方法
        //这题如果改变一下题意：
        //dp[j]表示，装满容量为j的背包，最少有dp【j】个
        int[] dp = new int[amount + 1];
        dp[0]=0;
        for(int i=1;i<=amount;i++){
            dp[i]=Integer.MAX_VALUE;
        }
        //System.out.println(dp[amount]);

        for(int i=0;i<coins.length;i++){
            for(int j=coins[i];j<=amount;j++){
                if(dp[j-coins[i]]!=Integer.MAX_VALUE)
                dp[j]=Math.min(dp[j-coins[i]]+1,dp[j]);
            }
        }
        return dp[amount]==Integer.MAX_VALUE?-1:dp[amount];
    }
}

279. 完全平方数

思想

完全背包问题。

背包的容量为n，物品为1到根号n，物品能够重复取

1.dp[j] ： 装满容量为j的背包，所需要的完全平方数的最少的数量为dp[j]

2.dp[j]= Math.min(dp[j-i*i]+1,dp[j])

3.初始化

dp[0]=0;

dp[1]=1;

4.遍历顺序

都可以，不管怎么样遍历，组合还是排列，求得是一个最小的值。

代码

class Solution {
    public int numSquares(int n) {
        //dp[j] 表示 为j的背包 装满的最小的数量为dp[j]
        //dp[j]=min(dp[j-i]+1,dp[j])
        int [] dp=new int[n+1];
        dp[0]=0;
        for(int i=1;i<=n;i++){
            dp[i]=Integer.MAX_VALUE;
        }
        for(int i=1;i*i<=n;i++){
            for(int j=i*i;j<=n;j++){
                if(dp[j-i*i]!=Integer.MAX_VALUE)
                dp[j]=Math.min(dp[j-i*i]+1,dp[j]);
            }
        }
        return dp[n];
    }
}