【1691. 堆叠长方体的最大高度】

news2024/10/7 5:24:35

来源：力扣（LeetCode）

描述：

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti]（下标从 0 开始）。请你从 cuboids 选出一个子集，并将它们堆叠起来。

如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。

返回 堆叠长方体 cuboids 可以得到的 最大高度 。

示例 1：

输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
输出：190
解释：
第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。

示例 2：

输入：cuboids = [[38,25,45],[76,35,3]]
输出：76
解释：
无法将任何长方体放在另一个上面。
选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。

示例 3：

输入：cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
输出：102
解释：
重新排列长方体后，可以看到所有长方体的尺寸都相同。
你可以把 11x7 的一面朝下，这样它们的高度就是 17 。
堆叠长方体的最大高度为 6 * 17 = 102 。

提示：

n == cuboids.length
1 <= n <= 100
1 <= widthi, lengthi, heighti <= 100

方法一：动态规划

思路与算法

由于题目要求长方体的高度最大，由此很容易想到将每个长方体的最长边做为高度是最优的，但这种堆叠方法是否正确需要进一步思考。假设两个长方体 r₁, r₂ 的长宽高分别为 (w₁, l₁, h₁) (w₂, l₂, h₂) ，且满足 w₁ ≤ w2, l₁ ≤ l₂, h₁ ≤ h₂，此时长方体 r₁ 一定可以堆叠在长方体 r₂ 之上，此时得到的高度为 h₁ + h₂ 。我们将长方体 r₁, r₂ 的长宽高按照从小到大的顺序重新进行排列为 (w₁′, l₁′, h₁′) 与 (w₂′, l₂′, h₂′) ，且满足 w₁′ ≤ l₁′ ≤ h₁′, w₁′ ≤ l₁′ ≤ h₁′ 。此时我们只需要证明 w₁′ ≤ w₂′, l₁′ ≤ l₂′, h₁′ ≤ h₂′，即可满足堆叠条件。证明如下：

根据之前的结论可知道 r₁ 中的最大值一定小于等于 r₂ 中的最大值，r₁ 中的最小值一定小于等于 r₂ 中的最小值，否则一定不会出现 w₁ ≤ w2, l₁ ≤ l₂, h₁ ≤ h₂，此时一定可以推出 w₁′ ≤ w₂′, l₁′ ≤ l₂′, h₁′ ≤ h₂′。此时我们假设 l₁′ > l₂′ ，则此时可以推出 w₁′ ≤ w₂′ ≤ l2′<l₁′ ≤ w₁′ ≤ w₂′ 。按照之前的推论可知 r₁ 中一定存在一个元素小于 w₂′ ，存在另外一个元素小于 l₂′ ，而此时小于等于 w₂′,l₂′ 的元素只有一个，与上述结论相矛盾，因此我们一定可以得出结论 l₁′ ≤ l₂′ 。因此 w₁′ ≤ w₂′,l₁′ ≤ l₂′, h₁′≤h₂′ 结论成立。

当按照长方体的三条边从小到大进行排序后，此时长方体的高度即对应了三条边中的最大值，那么整个长方体的堆叠高度之和一定不会大于每个长方体的最大边之和，因此最优的堆叠方法一定是基于最长边作为高度的。

我们下一步计算整个堆叠高度，我们可以设 dp[i] 表示以第 i 个长方体 (w_i′, l_i′, h_i′) 为最后一个长方体的最大堆叠高度，可以使用动态规划并写出状态转移方程：

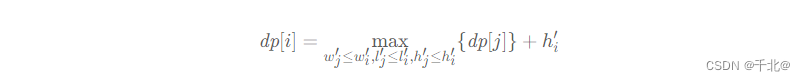
我们需要找到找到所有可以放置到 i 长方体之上的长方体 j，长方体 j 需要满足 w_j′ ≤ w_i′, l_j′ ≤ l_i′, h_j′ ≤ h_i′ 。如果不存在可以堆叠的长方体，此时 dp[i]=h_i′ ，最终最大的堆叠高度即为 max⁡(dp[i]) 。

如果想要实现上述的动态规划，必须保证当枚举到第 i 长方体时，所有可以堆叠在第 i 个长方体之上的长方体都应该枚举过，因此在动态规划之前，我们应保证所有满足可堆叠在第 i 个长方体之上的长方体排在 iii 之前，可以利用排序来解决这个问题。这里有非常多的排序方法，只要保证枚举关系的拓扑性即可，例如我们可以使用关键字 (w_i′, l_i′, h_i′) 排序，无论采用何种排序方法只需满足当 w_j′ ≤ w_i′, l_j′ ≤ l_i′, h_j′ ≤ h_i′ 时，一定满足 j ≤ i 即可。

代码：

class Solution {
public:
    int maxHeight(vector<vector<int>>& cuboids) {
        int n = cuboids.size();
        for (auto & v : cuboids) {
            sort(v.begin(), v.end());
        }
        sort(cuboids.begin(), cuboids.end(), [](const vector<int> & a,const vector<int> & b) {
            return a[0] + a[1] + a[2] < b[0] + b[1] + b[2];
        });
        int ans = 0;
        vector<int> dp(n);
        for (int i = 0; i < n; i++) {
            dp[i] = cuboids[i][2];
            for (int j = 0; j < i; j++) {
                if (cuboids[i][0] >= cuboids[j][0] && 
                    cuboids[i][1] >= cuboids[j][1] && 
                    cuboids[i][2] >= cuboids[j][2]) {
                    dp[i] = max(dp[i], dp[j] + cuboids[i][2]);
                }
            }
            ans = max(ans, dp[i]);
        }
        return ans;
    }
};

执行用时：12 ms, 在所有 C++ 提交中击败了74.41%的用户
内存消耗：8.8 MB, 在所有 C++ 提交中击败了72.44%的用户
复杂度分析
时间复杂度：O(n²) ，其中 n 表示长方体的个数。时间复杂度主要取决于排序与动态规划枚举，对每个长方体边的大小进行排序的总时间复杂度为 O(n)，对长方体进行排序的时间为 O(nlog⁡n) ，对于每个长方体我们都需要枚举所有可以堆叠其上的长方体，需要的时间为 O(n²) ，因此总的时间复杂度为 O(n²) 。
空间复杂度： O(n)，其中 n 表示长方体的个数。排序需要的栈空间为 O(log⁡n) ，存储每个长方体为底的最大高度需要的空间为 O(n)，因此总的空间复杂度为 O(n)。

方法二：记忆化搜索

思路与算法

与解法一同样的解题思路，我们还可以采用自顶向下的记忆化搜索，与方法一相比会减少无效状态，设 memo[i] 表示第 i 个长方体为顶部长方体的最大高度，我们依次尝试是否可以把当前的第 i 个长方体放置到第 j 个长方体的顶部。则此时我们可以得到递推公式如下:

我们求出以每个长方体为顶部的最大高度即可。

代码:

class Solution {
public:
    bool check(const vector<int> &a, const vector<int> &b) {
        return a[0] <= b[0] && a[1] <= b[1] && a[2] <= b[2];
    }

    int maxHeight(vector<vector<int>>& cuboids) {
        int n = cuboids.size();
        for (auto & v : cuboids) {
            sort(v.begin(), v.end());
        }
        sort(cuboids.begin(), cuboids.end(), [](const vector<int> & a, const vector<int> & b) {
            return a[0] + a[1] + a[2] < b[0] + b[1] + b[2];
        });

        vector<int> memo(n, -1);
        function<int(int, int)> dfs = [&](int top, int index)->int {
            if (index == cuboids.size()) {
                return 0;
            }
            if (top != -1 && memo[top] != -1) {
                return memo[top];
            }
            int height = dfs(top, index + 1);
            if (top == -1 || check(cuboids[top], cuboids[index])) {
                height = max(height, cuboids[index][2] + dfs(index, index + 1));
            }
            if (top != -1) {
                memo[top] = height;
            }
            return height;
        };
        return dfs(-1, 0);
    }
};

执行用时：12 ms, 在所有 C++ 提交中击败了74.41%的用户
内存消耗：9 MB, 在所有 C++ 提交中击败了16.14%的用户
复杂度分析
时间复杂度：O(n²)，其中 n 表示长方体的个数。时间复杂度主要取决于排序与动态规划枚举，对每个长方体边的大小进行排序的总时间复杂度为 O(n)，对长方体进行排序的时间为 O(nlog⁡n)，对于每个长方体我们都需要枚举所有可以堆叠在其下方的长方体，需要的时间为 O(n²)，因此总的时间复杂度为 O(n²)。
空间复杂度： O(n)，其中 n 表示长方体的个数。排序需要的栈空间为 O(log⁡n)，存储每个长方体为底的最大高度需要的空间为 O(n)，递归搜索最大深度为 O(n)。因此总的空间复杂度为 O(n)。
author：力扣官方题解