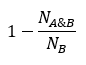多目标优化的基本概念

  习多目标优化的过程中，其中涉及相关概念如下：

Pareto 支配关系 (Pareto Dominance)：
	支配：对于多个目标值，随机自变量x1、x2，对于任意一个目标函数都存在f(x1)<f(x2)，则x1支配x2。
	弱支配：对于多个目标值，随机自变量x1、x2，对于目标函数有f(x1)≤f(x2)，且至少存在一个目标函数有g(x1)<g(x2)，则x1弱支配x2。
	互不支配：对于多个目标值，随机自变量x1、x2，使f(x1)≤f(x2)，同时，存在一个目标函数g(x1)>g(x2)，则x1和x2互不支配。

.

Pareto解 (Pareto Solution) 又称非支配解或不受支配解（nondominated solutions）
	在有多个目标时，由于存在目标之间的冲突和无法比较的现象，一个解在某个目标上是最好的，在其他的目标上可能是最差的。这些在改进任何目标函数的同时，必然会削弱至少一个其他目标函数的解称为非支配解或Pareto解。

.

Pareto最优解 (Pareto Optimal Solution)
	无法在改进任何目标函数的同时不削弱至少一个其他目标函数，这种解称作非支配解(nondominated solutions)或Pareto最优解(Pareto optimal solutions)。
	可以理解为：这种状态下，一旦使任何一个目标更优的时候就会损坏其他目标的利益。即，不削弱其他目标是任何目标无法改进的状态。

.

Pareto 集 (Pareto Set)
	一个多目标优化问题，对于一组给定的最优解集，如果这个集合中的解是相互非支配的，即两两不是支配关系，那么则称这个解集为Pareto Set 。

.
Pareto 前沿(Pareto Front)
	Pareto Set 中每个解对应的目标值向量组成的集合称之为Pareto Front, 简称为PF。

带精英策略的非支配排序的遗传算法(NSGA-II)

   NSGA-II 与简单的遗传算法的主要区别在于：该算法在选择算子执行之前根据个体之间的支配关系进行了分层。其选择算子、交叉算子和变异算子与简单遗传算法没有区别。

其中涉及算法有：
   快速非支配排序法：降低了算法的计算复杂度
   拥挤度和拥挤度比较算子，在快速排序后的同级比较中作为胜出标准，使准Pareto域中的个体能扩展到整个Pareto域，并均匀分布，保持了种群的多样性。
   引入精英策略，扩大采样空间。将父代种群与其产生的子代种群组合，共同竞争产生下一代种群，有利于保持父代中的优良个体进入下一代，并通过对种群中所有个体的分层存放，使得最佳个体不会丢失，迅速提高种群水平。

快速非支配排序法

   对于每个个体 i 都设有两个参数 n(i) 和 S(i)。n(i) 为在种群中支配个体 i 的解的个体数量（别的解支配个体 i 的数量）；S(i) 为被个体 i 所支配的解的个体集合（个体 i 支配别的解的集合）。

   1、首先，找到种群中所有 n(i)=0 的个体（种群中所有不被其他个体支配的个体 i），将它们存入当前集合F(1)；（找到种群中所有未被其他解支配的个体）

   2、对于当前集合 F(1) 中的每个个体 j，考察它所支配的个体集 S(j)，将集合 S(j) 中的每个个体 k 的 n(k) 减去1，即支配个体 k 的解个体数减1(因为支配个体 k 的个体 j 已经存入当前集 F(1) )；（对其他解除去被第一层支配的数量，即减一）

   3、如果 n(k)-1=0则将个体 k 存入另一个集H。最后，将 F(1) 作为第一级非支配个体集合，并赋予该集合内个体一个相同的非支配序 i(rank)，然后继续对 H 作上述分级操作并赋予相应的非支配序，直到所有的个体都被分级。

确定拥挤度：

   拥挤度：在种群中，给定点的周围个体的密度，用 $i_d$ 表示，它指出了在个体 i 周围包含个体 i 本身但不包含其他个体的长方形（以同一支配层的最近邻点作为顶点的长方形），如图所示：

拥挤度比较算子:

   从图中我们可以看出 $i_d$ 值较小时表示该个体周围比较拥挤。为了维持种群的多样性，我们需要一个比较拥挤度的算子以确保算法能够收敛到一个均匀分布的Pareto 面上。由于经过了排序和拥挤度的计算，群体中每个个体 i 都得到两个属性：非支配序 i(rank) 和拥挤度 $i_d$，则定义偏序关系${\prec }_n$ ：当满足条件 $i(rank)<i_d$，或满足 $i(rank)=i_d$ 且 $i_d$ > $j_d$时，定义，$x{\prec }_{n}y$ 。也就是说：如果两个个体的非支配排序不同，取排序号较小的个体(分层排序时，先被分离出来的个体)；如果两个个体在同一级，取周围较不拥挤的个体。

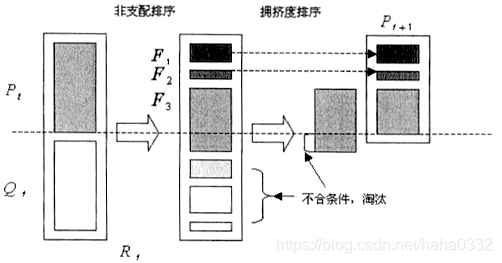
(2) 算法流程
   首先，随机初始化一个父代种群P(0)，并将所有个体按非支配关系排序且指定一个适应度值，如：可以指定适应度值等于其非支配序 i(rank)，则1是最佳适应度值。然后，采用选择、交叉、变异算子产生下一代种群Q(0)，大小为N。首先将第 t 代产生的新种群Q(t)与父代P(t)合并组成R(t)，种群大小为2N。然后R(t) 进行非支配排序，产生一系列非支配集 F(t) 并计算拥挤度。由于子代和父代个体都包含在 R(t) 中，则经过非支配排序以后的非支配集 F(1) 中包含的个体是 R(t) 中最好的，所以先将 F(1) 放入新的父代种群 P(t+1) 中。如果 F(1) 的大小小于N，则继续向 P(t+1) 中填充下一级非支配集 F(2)，直到添加 F(3) 时，种群的大小超出N，对 F(3) 中的个体进行拥挤度排序(sort(F(3),))，取靠前的个体，使 P(t+1) 个体数量达到N。然后通过遗传算子(选择、交叉、变异)产生新的子代种群 Q(t+1)。

如下图：