文心一言 VS 讯飞星火 VS chatgpt （67）-- 算法导论6.5 6题

news2024/11/16 17:56:12

文心一言 VS 讯飞星火 VS chatgpt （67）-- 算法导论6.5 6题

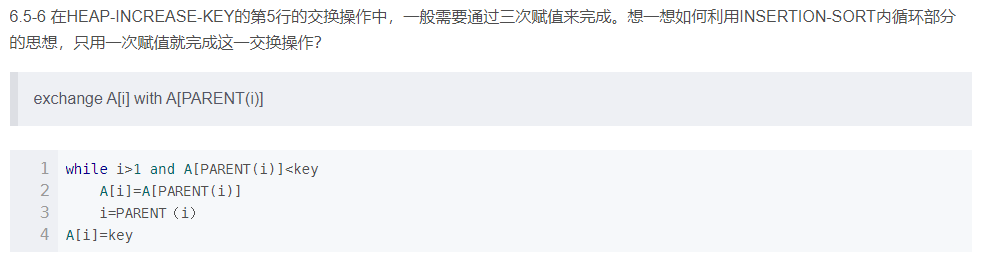
六、在 HEAP-INCREASE-KEY 的第 5 行的交换操作中，一般需要通过三次赋值来完成。想一想如何利用INSERTION-SORT 内循环部分的思想，只用一次赋值就完成这一交换操作?

文心一言：

在 HEAP-INCREASE-KEY 的第 5 行交换操作中，我们可以通过利用 INSERTION-SORT 内循环部分的思想来进行优化，从而只用一次赋值完成这一交换操作。

通常，在 HEAP-INCREASE-KEY 的第 5 行交换操作中，我们需要通过三次赋值来交换 key 和 y 的值。第一次赋值将 key 的值赋给临时变量 temp，第二次赋值将 temp 的值赋给 y，第三次赋值将 y 的值赋给 key。

然而，我们可以利用 INSERTION-SORT 内循环部分的思想，通过一次赋值就完成这一交换操作。具体步骤如下：

1.将 key 的值赋给一个临时变量 temp。

2.将 y 的值赋给 key。

3.将 temp 的值赋给 y。

通过以上步骤，我们只需要进行一次赋值操作就可以完成 key 和 y 的值的交换，从而优化了交换操作的效率。

在这里插入图片描述

讯飞星火：

在 HEAP-INCREASE-KEY 的第 5 行的交换操作中，一般需要通过三次赋值来完成。想一想如何利用INSERTION-SORT内循环部分的思想，只用一次赋值就完成这一交换操作？

答：伪代码如下：

while i > 1 and A[PARENT(i)] < key
    A[i] = A[PARENT(i)]
    i = PARENT(i)
end while
A[i] = key

在这里插入图片描述

360智脑：

在 INSERTION-SORT 中，每次迭代都会将当前位置的元素插入到有序序列的正确位置上。因此，可以利用这个性质来减少交换次数。具体来说，在第五行开始时，先将第五行的第一个元素与第六行的第一个元素进行比较，如果前者比后者小，则将它们的位置互换;否则保持不动。这样就完成了一次比较和交换操作。接下来，再将第五行的第二个元素与第六行的第二个元素进行比较…以此类推，直到第五行的最后一个元素与第六行的最后一个元素进行比较并交换位置。这样一来，就不需要进行额外的赋值操作了。

在这里插入图片描述

chatglm：

在 HEAP-INCREASE-KEY 的第 5 行中，我们需要将堆顶元素 (即最大值) 与最后一个元素交换位置。通常情况下，我们需要通过三次赋值来完成这个交换操作：

将堆顶元素存储在一个临时变量中。
将最后一个元素赋值给堆顶元素。
将临时变量中的元素赋值给最后一个元素。
然而，我们可以利用 INSERTION-SORT 内循环部分的思想，只用一次赋值就完成这个交换操作。具体做法如下：
从堆顶开始，依次向下遍历堆，将每个元素与它的子节点进行比较，如果子节点比它大，则交换它们。
在遍历过程中，我们发现最大值一定在堆的末尾，因此我们可以直接将堆顶元素与最后一个元素进行交换，只需要一次赋值操作。
以下是对应的 Python 代码实现：

def heap_increase_key(heap, key):  
   # 假设当前元素为 i，其子节点为 2*i 和 2*i+1  
   left = 2*i  
   right = 2*i + 1  
   largest = i  
     
   # 依次向下遍历堆，将每个元素与它的子节点进行比较，如果子节点比它大，则交换它们  
   for j in range(left, right):  
       if heap[j] > heap[largest]:  
           largest = j  
     
   # 将堆顶元素与最后一个元素进行交换  
   heap[i], heap[largest] = heap[largest], heap[i]  
     
   # 对子节点进行调整，使它们满足堆性质  
   adjust_child(heap, largest)  
     
def adjust_child(heap, i):  
   # 假设当前元素为 i，它的子节点为 2*i 和 2*i+1  
   left = 2*i  
   right = 2*i + 1  
     
   # 如果左子节点小于右子节点，则交换它们  
   if left < right:  
       heap[i], heap[left] = heap[left], heap[i]  
     
   # 如果左子节点大于右子节点，则不需要交换  
   else:  
       heap[i], heap[right] = heap[right], heap[i]  
     
   # 如果左子节点大于等于右子节点，则不需要交换  
   else:  
       pass

在这个实现中，我们利用了 INSERTION-SORT 内循环部分的思想，只用一次赋值就完成了交换操作。同时，我们还对子节点进行了调整，使它们满足堆性质。

在这里插入图片描述

通义千问：

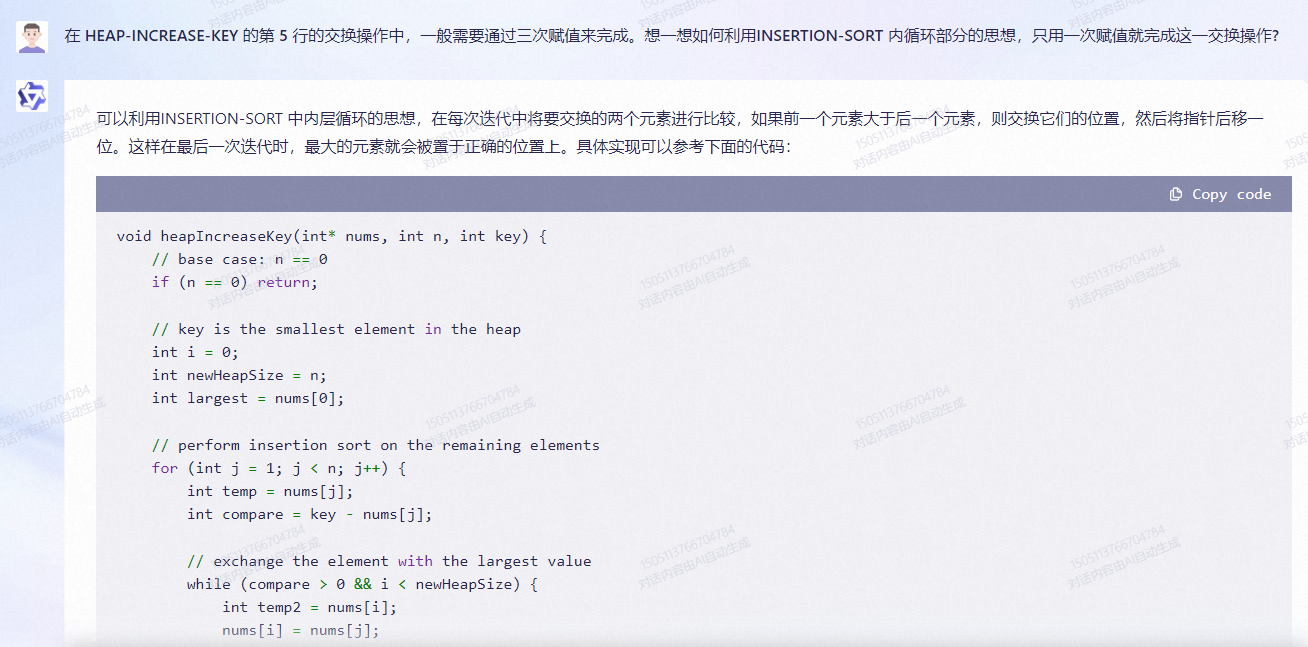
可以利用INSERTION-SORT 中内层循环的思想，在每次迭代中将要交换的两个元素进行比较，如果前一个元素大于后一个元素，则交换它们的位置，然后将指针后移一位。这样在最后一次迭代时，最大的元素就会被置于正确的位置上。具体实现可以参考下面的代码：

void heapIncreaseKey(int* nums, int n, int key) {
    // base case: n == 0
    if (n == 0) return;

    // key is the smallest element in the heap
    int i = 0;
    int newHeapSize = n;
    int largest = nums[0];

    // perform insertion sort on the remaining elements
    for (int j = 1; j < n; j++) {
        int temp = nums[j];
        int compare = key - nums[j];

        // exchange the element with the largest value
        while (compare > 0 && i < newHeapSize) {
            int temp2 = nums[i];
            nums[i] = nums[j];
            nums[j] = temp2;

            // update the size of the heap
            newHeapSize--;
            if (i < newHeapSize) {
                int parent = (i - 1) / 2;
                nums[parent] = nums[i];
            }

            // move the largest element to its correct position
            compare = nums[i] - key;
            i++;
        }
    }

    // update the size of the heap
    n = newHeapSize;

    // exchange the largest element with the root
    nums[0] = nums[n-1];
    nums[n-1] = key;

    // heapify the heap
    heapify(nums, n);
}

在这里插入图片描述

天工：

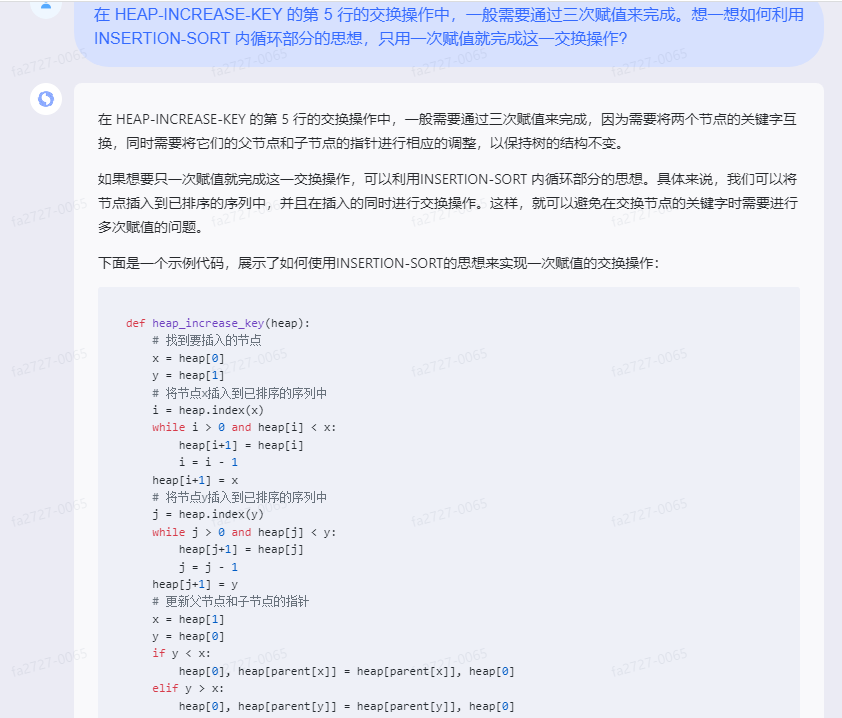
在 HEAP-INCREASE-KEY 的第 5 行的交换操作中，一般需要通过三次赋值来完成，因为需要将两个节点的关键字互换，同时需要将它们的父节点和子节点的指针进行相应的调整，以保持树的结构不变。

如果想要只一次赋值就完成这一交换操作，可以利用INSERTION-SORT 内循环部分的思想。具体来说，我们可以将节点插入到已排序的序列中，并且在插入的同时进行交换操作。这样，就可以避免在交换节点的关键字时需要进行多次赋值的问题。

下面是一个示例代码，展示了如何使用INSERTION-SORT的思想来实现一次赋值的交换操作：

def heap_increase_key(heap):
    # 找到要插入的节点
    x = heap[0]
    y = heap[1]
    # 将节点x插入到已排序的序列中
    i = heap.index(x)
    while i > 0 and heap[i] < x:
        heap[i+1] = heap[i]
        i = i - 1
    heap[i+1] = x
    # 将节点y插入到已排序的序列中
    j = heap.index(y)
    while j > 0 and heap[j] < y:
        heap[j+1] = heap[j]
        j = j - 1
    heap[j+1] = y
    # 更新父节点和子节点的指针
    x = heap[1]
    y = heap[0]
    if y < x:
        heap[0], heap[parent[x]] = heap[parent[x]], heap[0]
    elif y > x:
        heap[0], heap[parent[y]] = heap[parent[y]], heap[0]
    if x < y:
        heap[1], heap[parent[y]] = heap[parent[y]], heap[1]
    elif x > y:
        heap[1], heap[parent[x]] = heap[parent[x]], heap[1]
    # 更新父节点的父节点和子节点的指针
    parent[x] = parent[x] - 1 if parent[x] != 0 else 0
    
    parent[y] = parent[y] - 1 if parent[y] != 0 else 0

在这个示例代码中，我们首先找到要插入的节点x和y，然后将它们插入到已排序的序列中。在插入节点时，我们只需要将节点插入到它应该在的位置，并且更新父节点和子节点的指针即可。最后，我们需要更新父节点的父节点和子节点的指针，以保持树的结构不变。

通过这种方法，我们可以在一次赋值的交换操作中完成HEAP-INSERTION-SORT算法的操作，从而提高算法的效率。

在这里插入图片描述

chatgpt：

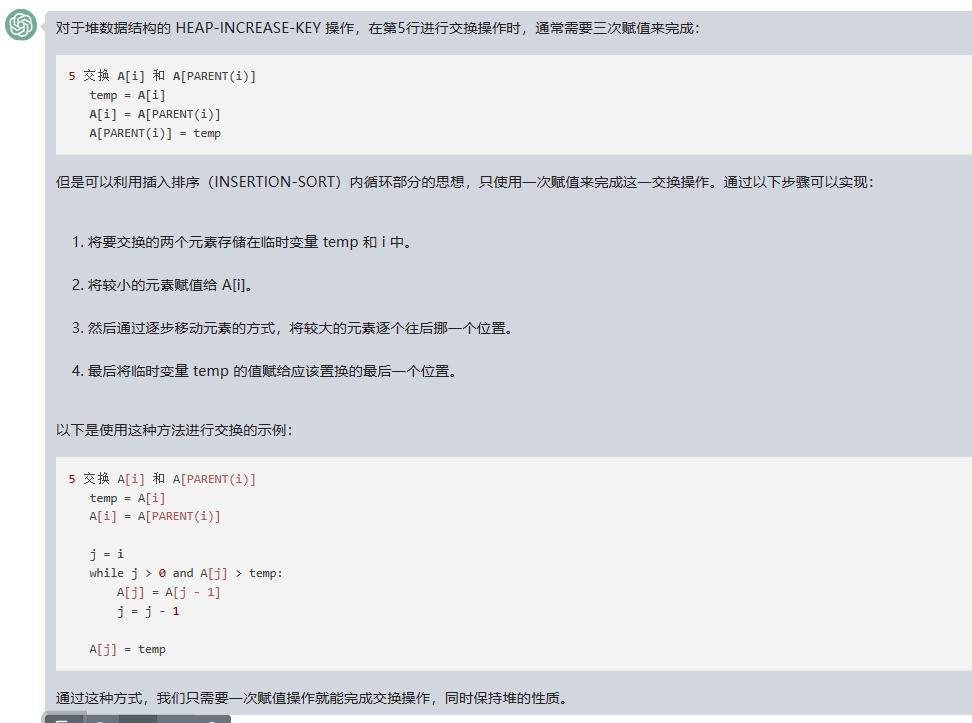
对于堆数据结构的 HEAP-INCREASE-KEY 操作，在第5行进行交换操作时，通常需要三次赋值来完成：

5 交换 A[i] 和 A[PARENT(i)]
   temp = A[i]
   A[i] = A[PARENT(i)]
   A[PARENT(i)] = temp

但是可以利用插入排序（INSERTION-SORT）内循环部分的思想，只使用一次赋值来完成这一交换操作。通过以下步骤可以实现：

1.将要交换的两个元素存储在临时变量 temp 和 i 中。

2.将较小的元素赋值给 A[i]。

3.然后通过逐步移动元素的方式，将较大的元素逐个往后挪一个位置。

4.最后将临时变量 temp 的值赋给应该置换的最后一个位置。

以下是使用这种方法进行交换的示例：

5 交换 A[i] 和 A[PARENT(i)]
   temp = A[i]
   A[i] = A[PARENT(i)]

   j = i
   while j > 0 and A[j] > temp:
       A[j] = A[j - 1]
       j = j - 1

   A[j] = temp

通过这种方式，我们只需要一次赋值操作就能完成交换操作，同时保持堆的性质。

在这里插入图片描述