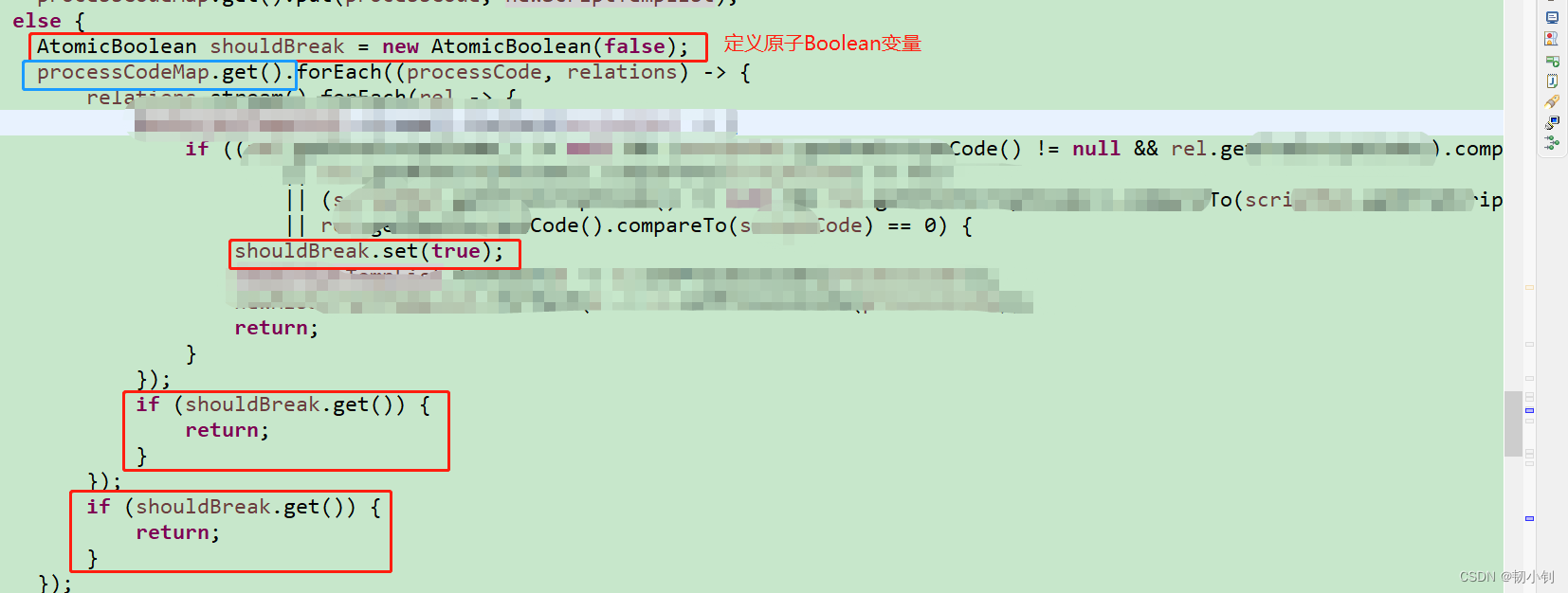
距离度量
衡量两条向量之间的距离,可以将某一张图片通过特征提取来转换为一个特征向量。衡量两张图片的相似度就可以通过衡量这两张图片对应的两个特征向量之间的距离来判断了。
1.欧式距离
欧式距离可以简单理解为两点之间的直线距离。对于两个n维空间点
a
=
(
x
1
,
x
2
,
…
,
x
n
)
a=(x_1, x_2, …, x_n)
a=(x1,x2,…,xn)和
b
=
(
y
1
,
y
2
,
…
,
y
n
)
b=(y_1, y_2, …,y_n)
b=(y1,y2,…,yn),它们之间的欧式距离定义如下:
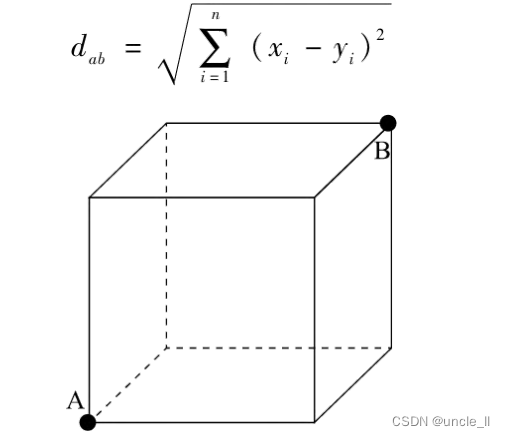
三维空间中边长为1的立方体
在三维空间中的边长为1的一个立方体,它的对角线之间的距离为 3 \sqrt3 3,如图2-1所示。这个距离值就是欧氏距离,也就是平时说得最多的“距离”。在图2-1中,若以A点为坐标原点建立空间直角坐标系,那么A点的位置为 ( 0 , 0 , 0 ) (0,0,0) (0,0,0),B点的位置为 ( 1 , 1 , 1 ) (1,1,1) (1,1,1),则A点与B点之间的距离也就是的模长:
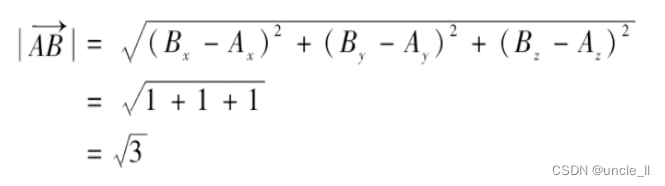
2.曼哈顿距离
曼哈顿距离最初指的是区块建设的城市(如曼哈顿)中,两个路口间的最短行车距离,因此也被称为城市街区距离。对于两个n维空间 a = ( x 1 , x 2 , … , x n ) a=(x_1, x_2, …,x_n) a=(x1,x2,…,xn) 和 b = ( y 1 , y 2 , … , y n ) b=(y_1, y_2, …, y_n) b=(y1,y2,…,yn),它们之间的曼哈顿距离定义如下:
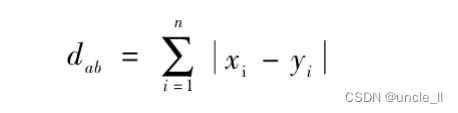
曼哈顿距离公式还是比较容易理解的,例如a=[1,2,3],b=[2,3,4],那么两个向量之间的曼哈顿距离可以表示如下:
∣ 1 − 2 ∣ + ∣ 2 − 3 ∣ + ∣ 3 − 4 ∣ = 3 |1-2| + |2-3| + |3-4| = 3 ∣1−2∣+∣2−3∣+∣3−4∣=3
求解曼哈顿距离的过程就是求两条向量中每个对应位置的元素之差的绝对值,然后将其求和的过程。
3.余弦距离
余弦距离指的是向量空间中两个向量间的夹角的余弦值,又称作余弦相似度。对于两个n维空间 a = ( x 1 , x 2 , … , x n ) a=(x_1, x_2, …,x_n) a=(x1,x2,…,xn) 和 b = ( y 1 , y 2 , … , y n ) b=(y_1, y_2, …, y_n) b=(y1,y2,…,yn),它们的余弦距离定义如下:
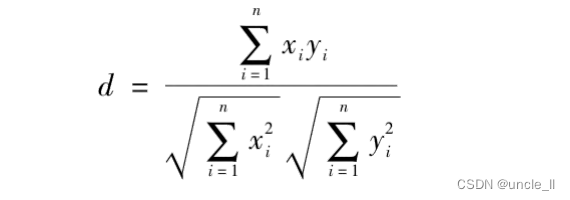
可以根据向量之间点乘的公式反推一下余弦距离的表达式, 对于两个向量 a = [ 1 , 2 , 3 ] a=[1,2,3] a=[1,2,3]与 b = [ 4 , 5 , 6 ] b=[4,5,6] b=[4,5,6],它们之间点积的计算过程如下:
a ⋅ b = ∣ a ∣ ⋅ ∣ b ∣ ⋅ c o s θ a \cdot b = |a|\cdot|b|\cdot cosθ a⋅b=∣a∣⋅∣b∣⋅cosθ
那么,这两个向量之间夹角θ的余弦值可以表示为:
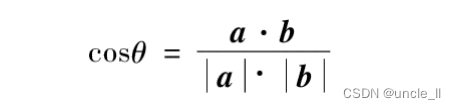
这两个向量之间夹角的余弦值就是这两个向量之间的余弦相似度。将向量的计算过程带入式中,可以得到这两条向量之间的余弦相似度:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MethOwdn-1690541816242)(C:\Users\DELL-3020\AppData\Roaming\Typora\typora-user-images\image-20230727184904795.png)]](https://img-blog.csdnimg.cn/dba411757d0a454b9b17fc38bfa1a8d4.png)
余弦相似度的数值范围也就是余弦值的范围,即 [ − 1 , 1 ] [-1, 1] [−1,1],这个值越高也就说明相似度越大。可以看到,这两条向量之间的相似度非常接近1,可以说是非常相似的。也可以想象到,在三维空间中,这两条向量的差距其实并不是非常大,这也从侧面印证了余弦相似度的数值含义。
值得一提的是,有些时候希望这个数值的范围在 [ 0 , 1 ] [0, 1] [0,1]这个区间中,也就是对结果进行归一化处理。这个归一化过程可以利用余弦值的性质来完成:
c o s θ ′ = 0.5 + 0.5 ∗ c o s θ cosθ' = 0.5 + 0.5 * cosθ cosθ′=0.5+0.5∗cosθ
余弦相似度是一种非常常用的衡量向量之间距离的方式,常用在人脸识别等特征相似度度量的场景中。
4.汉明距离
汉明距离在信息论中更常用,表示的是两个等长度的字符串中位置相同但字符不同的位置个数,。如字符串“011001”与字符串“101100”之间的汉明距离为4,也就是这两个字符串之间存在4个位置的不同,分别出现在第1、第2、第4和第6个字符的位置上。
汉明距离也可以用在某些图像相似度识别场景,如有种图像相似性识别算法叫作感知哈希算法(Perceptual Hash Algorithm),该算法可以将图片映射为一个哈希字符串,比较两个图片之间的相似度就可以通过判断两个哈希字符串之间不一致的位置有多少来实现,也就是计算汉明距离的过程。
5.杰卡德距离
杰卡德Jaccard相似系数计算数据集之间的相似度,计算方式为:数据集交集的个数和并集个数的比值。计算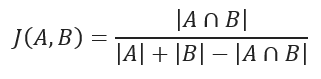
杰卡德距离是用来衡量两个数据集差异性的一种指标,被定义为 1 减去杰卡德相似系数。对于二值变量,杰卡德距离等价于谷本系数。
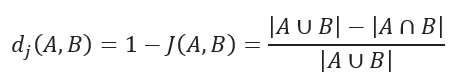
杰卡德距离适合字符串相似性度量。
6.谷本距离
谷本距离Tanimoto主要用于衡量二值变量,对于二值变量,谷本距离公式可表示为:
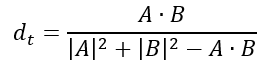
在 Milvus 中,谷本距离仅支持二值变量。
值域从 0 到正无穷。
对于二值变量,谷本系数等价于杰卡德距离:
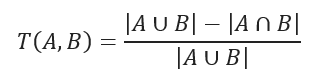
对于二值变量,谷本系数值域为 0 到+1(+1 的相似度最高)
7.超结构
超结构superstructure主要用来计算某化学结构与其超结构的相似度,值越小则相似度越大。
超结构的公式可表示为:
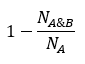
其中
- 分子式 B 是分子式 A 的超结构。
- N A N_A NA 表示分子式 A 的化学指纹中二进制位的数量。
- N B N_B NB 表示分子式 B 的化学指纹中二进制位的数量。
- N A & B N_{A\&B} NA&B 表示分子式 A 和 B 的化学指纹中共有的二进制位的数量。
8.子结构
子结构substructure主要用来计算某化学结构与其子结构的相似度,值越小则相似度越大
子结构的公式可表示为:
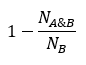
其中
- 分子式 B 是分子式 A 的子结构。
- N A N_A NA 表示分子式 A 的化学指纹中二进制位的数量。
- N B N_B NB 表示分子式 B 的化学指纹中二进制位的数量。
- N A & B N_{A\&B} NA&B 表示分子式 A 和 B 的化学指纹中共有的二进制位的数量。