小波变换

小波变换（Wavelet Transform）是一种数学信号处理技术，用于将信号或图像分解为不同频率的小波成分，从而可以在不同时间尺度上分析信号的特征。小波变换具有许多重要的特性，使其在许多领域中有广泛的应用。

小波变换的意义包括以下几个方面：

1. 多尺度分析：小波变换可以在不同的时间尺度上分析信号，这意味着它可以同时提供关于信号的短时和长时特征信息。这使得小波变换在时频域分析中具有优势，特别是对于非平稳信号的处理。

2. 局部特征提取：小波变换是一种局部分析方法，它可以有效地捕获信号的局部特征，如突变、边缘等。相比之下，傅里叶变换是一种全局分析方法，往往无法提供局部特征信息。

3. 压缩和去噪：小波变换可以将信号分解为多个小波系数，其中包含不同频率的信息。通过适当选择小波系数，可以实现信号的压缩和去噪，去除噪声和冗余信息，从而提高信号处理的效果。

4. 图像处理：小波变换在图像处理中也有重要的应用。它可以用于图像压缩、边缘检测、纹理分析等任务，同时保持图像的局部特征和结构信息。

5. 特征提取：小波变换可以用于特征提取，从信号或图像中提取有用的特征信息，用于分类、识别和模式匹配等任务。

6. 数据分析：小波变换在数据分析中有广泛的应用，包括金融市场分析、生物医学信号处理、地震信号处理等领域。

小波变换是一种强大的数学工具，可以用于多尺度分析、特征提取、信号压缩和去噪等多个领域。它的应用涵盖了信号处理、图像处理、数据分析和模式识别等广泛领域，为我们理解信号的时频特性、提取重要特征和优化数据处理提供了重要手段。

小波变换（Wavelet Transform）可以用数学公式表示为以下形式：

给定一个连续函数或离散信号 $f(t)$，小波变换是通过将原始信号与一组小波基函数进行内积运算得到的。这些小波基函数是原始信号在不同频率和时间尺度上的缩放和平移版本。

连续小波变换（Continuous Wavelet Transform，CWT）的数学公式为：

$$CWT(a,b)={\int }_{-\infty }^{\infty }f(t){\psi }^{\ast }\left(\frac{t-b}{a}\right)dt$$

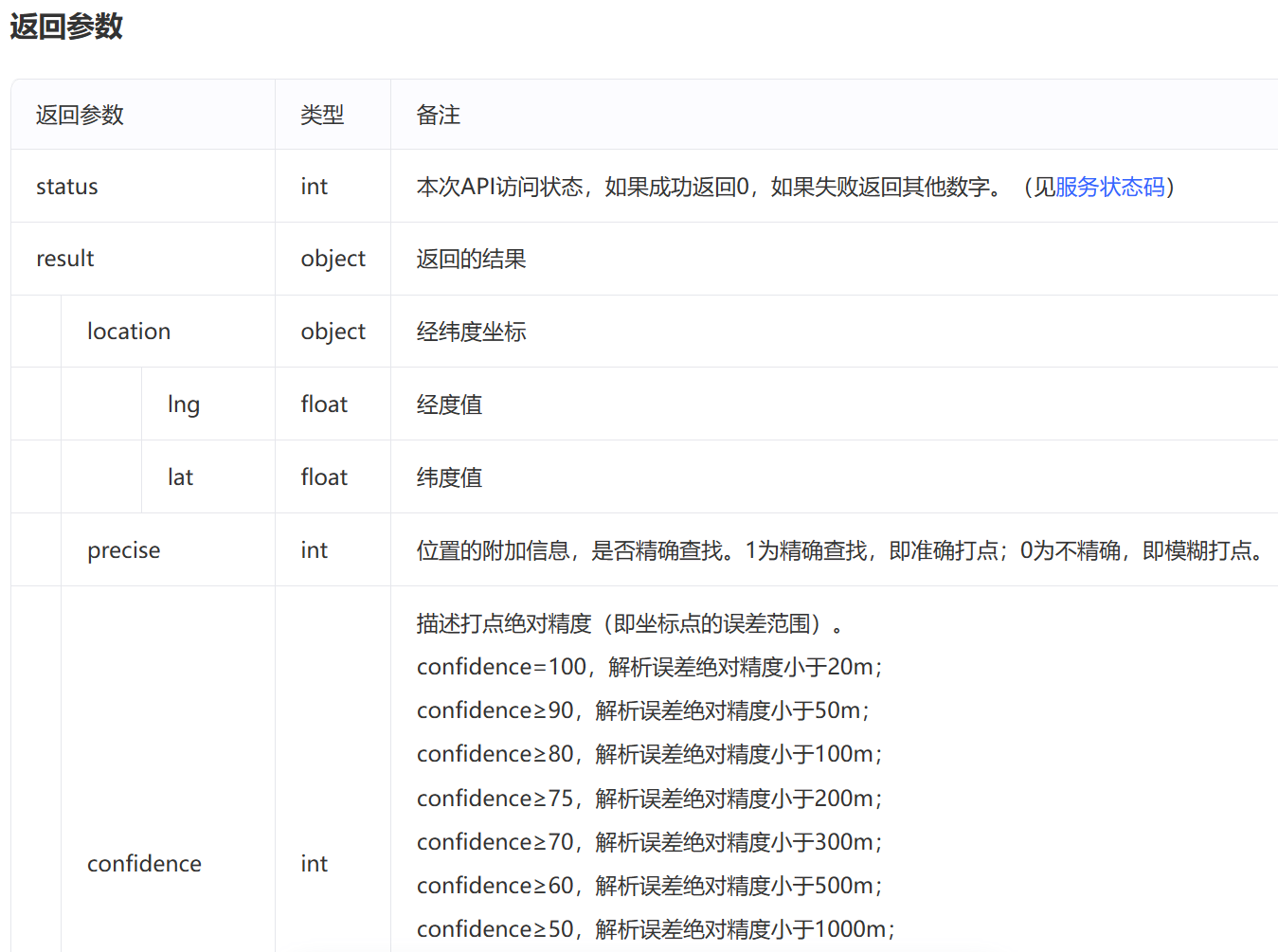
其中，$CWT(a,b)$ 是连续小波变换的结果，$a$ 和 $b$ 是小波基函数的缩放因子和平移因子，${\psi }^{\ast }(t)$ 是复共轭小波基函数。

复共轭小波基函数是小波变换中的一个重要概念。在小波变换中，我们通常使用两类小波基函数：一个是正向小波基函数（Mother Wavelet），另一个是复共轭小波基函数（Complex Conjugate Wavelet）。

设正向小波基函数为 $\psi (t)$，复共轭小波基函数为 ${\psi }^{\ast }(t)$。复共轭小波基函数是与正向小波基函数相对应的共轭复数函数。

数学上，复共轭小波基函数可以表示为：

$${\psi }^{\ast }(t)={\psi }^{\ast }(-t)$$

其中，${\psi }^{\ast }(-t)$ 表示对 $\psi (t)$ 中的每个点取共轭复数。换句话说，复共轭小波基函数是通过将正向小波基函数 $\psi (t)$ 中的每个点取共轭而得到的。这意味着复共轭小波基函数在时间域上是对称的，其实部和虚部都是奇函数。

在小波变换的计算过程中，复共轭小波基函数与信号进行内积运算，用于计算小波变换的实部和虚部部分，从而获得更完整的频率信息。

复共轭小波基函数在小波变换的正交性和完备性等性质中起到重要作用，确保小波变换的精确性和有效性。同时，复共轭小波基函数也在许多小波变换的应用中发挥着重要的作用，如信号压缩、图像处理和特征提取等领域。

离散小波变换（Discrete Wavelet Transform，DWT）则是通过对信号进行多级的低通滤波和高通滤波得到的。对于长度为 $N$ 的离散信号 $x[n]$，DWT 的数学公式为：

$$\begin{array}{rl}c{A}_j[k]& =\sum _{n=0}^{N-1}x[n]\cdot \frac{1}{\sqrt{2}}\cdot \psi \left(\frac{n-2k}{2^j}\right)\\ c{D}_j[k]& =\sum _{n=0}^{N-1}x[n]\cdot \frac{1}{\sqrt{2}}\cdot \varphi \left(\frac{n-2k}{2^j}\right)\end{array}$$

其中，$c{A}_j[k]$ 和 $c{D}_j[k]$ 分别是第 $j$ 级近似子带（Approximation Coefficients）和细节子带（Detail Coefficients），$k$ 表示子带的索引，$j$ 表示变换的级数。$\psi$ 和 $\varphi$ 是小波基函数和尺度函数，$\cdot$ 表示卷积运算。

通过多级的低通和高通滤波，DWT 可以将信号分解为不同频率的子带，从而实现多尺度分析。同时，通过对子带系数进行阈值处理和逆变换，可以实现信号的压缩和去噪等应用。

综上所述，小波变换是一种灵活且强大的信号处理技术，可以用于时频分析、信号压缩、去噪和特征提取等多个领域。它的数学公式描述了小波基函数与信号之间的变换关系，通过这种变换可以获得信号的不同频率和时间尺度上的特征信息。

程序实现

实现二维离散小波变换（2D-DWT），我们可以使用Python的pywt库，它提供了对小波变换的支持。首先，确保已经安装了pywt库，可以使用以下命令安装：

pip install PyWavelets

接下来，我们将给出一个示例代码，用于对一个二维图像进行小波变换。

import pywt
import numpy as np
import matplotlib.pyplot as plt

# blur.png
image = cv2.imread('blur.png', 0)

# 进行二维离散小波变换（2D-DWT）
coeffs = pywt.dwt2(image, 'haar')

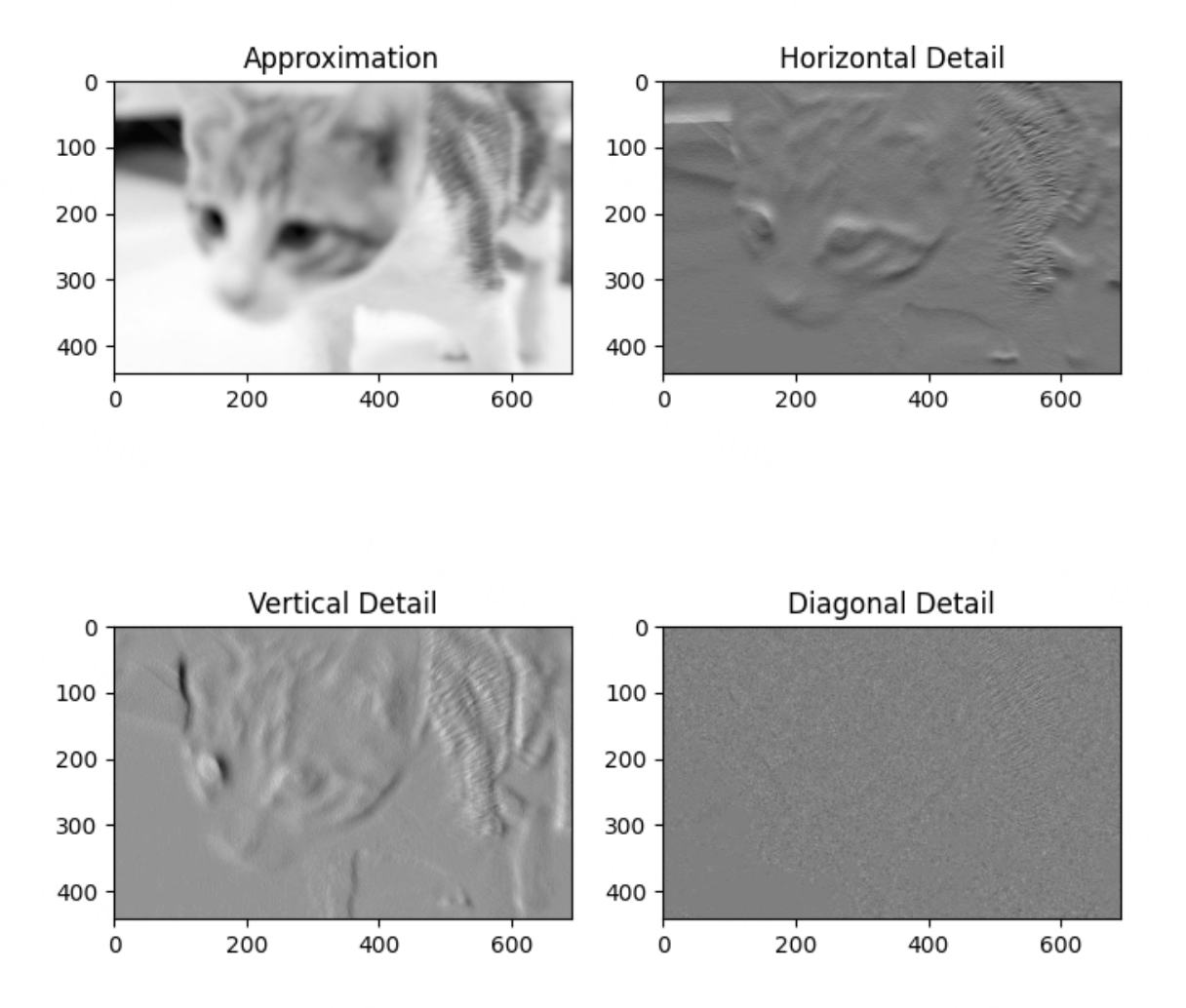
# 从结果中获取近似子带和细节子带
cA, (cH, cV, cD) = coeffs

# 打印结果
print("近似子带：")
print(cA)
print("\n水平细节子带：")
print(cH)
print("\n垂直细节子带：")
print(cV)
print("\n对角细节子带：")
print(cD)

# 可视化结果
plt.figure(figsize=(8, 8))
plt.subplot(2, 2, 1)
plt.imshow(cA, cmap='gray')
plt.title('Approximation')
plt.subplot(2, 2, 2)
plt.imshow(cH, cmap='gray')
plt.title('Horizontal Detail')
plt.subplot(2, 2, 3)
plt.imshow(cV, cmap='gray')
plt.title('Vertical Detail')
plt.subplot(2, 2, 4)
plt.imshow(cD, cmap='gray')
plt.title('Diagonal Detail')
plt.show()

子带

pywt.dwt2是pywt库中实现的二维离散小波变换（2D-DWT）函数。让我们通过数学公式来解释这个函数的作用：

给定一个2D数组data，我们可以将其表示为一个二维网格，其中每个元素表示一个像素的灰度值。2D-DWT的目标是将这个二维数组分解为多个子带，每个子带代表原始图像的不同部分或特征。具体地说，2D-DWT将输入的二维数组data分解为以下四个子带：

1. 近似子带（Approximation，记为cA）：表示原始图像的低频部分，包含图像中的整体结构和大致形状信息。

2. 水平细节子带（Horizontal Detail，记为cH）：表示图像中水平方向的高频信息，包括边缘和细节的水平变化。

3. 垂直细节子带（Vertical Detail，记为cV）：表示图像中垂直方向的高频信息，包括边缘和细节的垂直变化。

4. 对角细节子带（Diagonal Detail，记为cD）：表示图像中对角方向的高频信息，包括边缘和细节的对角变化。

这些子带可以用数学公式表示为：

cA：近似子带
cH：水平细节子带
cV：垂直细节子带
cD：对角细节子带

pywt.dwt2函数使用指定的小波（wavelet）对输入的图像data进行2D离散小波变换。其中，mode参数表示信号扩展模式，可以选择不同的模式进行计算。axes参数用于指定要进行变换的轴（即图像的维度）。函数返回近似子带cA和包含水平、垂直和对角细节子带的元组cH, cV, cD。

在示例中，我们使用Haar小波对其进行2D-DWT变换。

请注意，实际应用中，我们通常使用真实的图像数据，并根据不同的任务选择适合的小波函数。

数学公式

2D离散小波变换（2D-DWT）的数学公式可以用以下方式表示：

给定一个二维离散信号（图像） $f(x,y)$，其中 $(x,y)$ 表示图像的坐标，2D-DWT 将其分解为近似子带（Approximation, $cA$）和三个细节子带（Details）：水平细节子带（Horizontal Detail, $cH$）、垂直细节子带（Vertical Detail, $cV$）和对角细节子带（Diagonal Detail, $cD$）。

数学公式表示为：

$$\begin{array}{rl}cA& =(c{A}_{LL},c{A}_{LH},c{A}_{HL},c{A}_{HH})\\ cH& =(c{H}_{LL},c{H}_{LH},c{H}_{HL},c{H}_{HH})\\ cV& =(c{V}_{LL},c{V}_{LH},c{V}_{HL},c{V}_{HH})\\ cD& =(c{D}_{LL},c{D}_{LH},c{D}_{HL},c{D}_{HH})\end{array}$$

其中，$c{A}_{LL},c{H}_{LL},c{V}_{LL},c{D}_{LL}$ 是具有更低空间分辨率的近似子带和细节子带，分别代表水平、垂直和对角方向的低频信息。而 $c{A}_{LH},c{H}_{LH},c{V}_{LH},c{D}_{LH}$ 分别代表水平、垂直和对角方向的高频信息。

在实际应用中，通常会对近似子带进行进一步的分解，即多级小波变换，以获得更多层次的细节信息。2D-DWT 是图像处理和压缩中常用的技术，它允许我们在不同频率和空间尺度上分析图像内容，并用于多种图像处理任务。