汉诺塔(Tower of Hanoi)源于印度传说中,大梵天创造世界时造了三根金钢石柱子,其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
汉诺塔递归算法
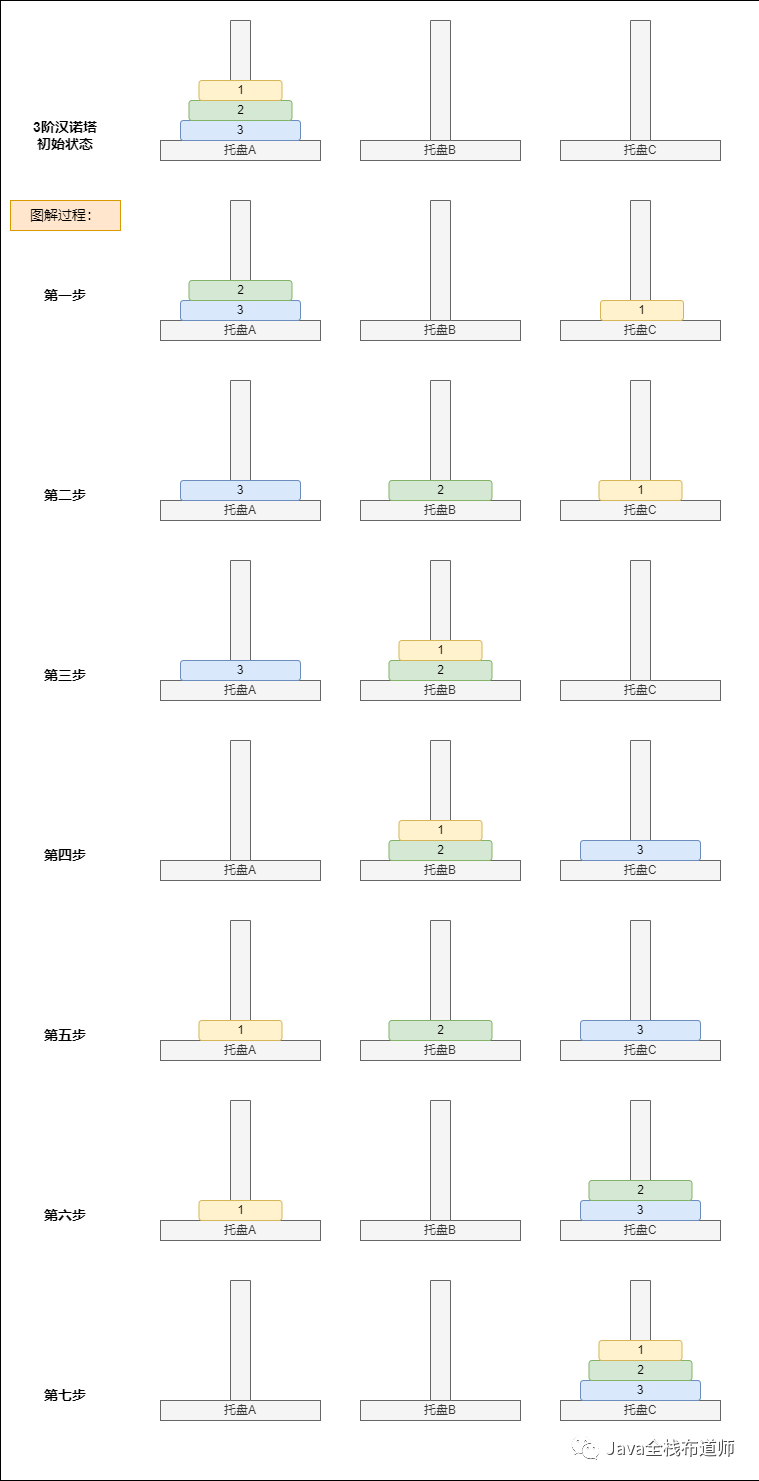
3阶汉诺塔移动步骤:
汉诺塔解法思路
一个规模为n的问题,可以拆成互相独立且与原问题形式相同的子问题的问题,可以采用递归方式解决子问题,然后将各个子问题的解合并得到原问题的解(分而治之思想)。
理解过程
如图,3阶的一共需要七步,
因为盘子3是最大的,所以所有盘子都可放在它上面,所以我们可以忽略盘子3,既是把“前三步”看做一个整体,完成2阶移动即可,移动目标是从A移动到B(伪C);
接着执行第四步,从A移到C,此时最大的盘就完成移动了,因为是最大,所以所有盘子都可以移到C,可以忽略盘子3,此时,后续的操作可以将3阶看成2阶来处理了;
“前三步”将盘子1和2,从A移到B了,托盘A和托盘B是相对来说的,此时的托盘B可以看做是托盘A,所以“后三步”2阶移动和普通的2阶移动步骤一样,移动目标是B(伪A)到C。
从上面分析可以知道,所有的移动都是从“A”移动到“C”,只是第一大步和最后一大步是要交换位置,分别是C交换成B、B交换从A(看代码不太懂时,回来看这里)
当n=1时,只需托盘A直接移到托盘C(这是递归问题的出口); 当n>1时,需要借助另一托盘来移动,将n个圆盘由A移到C上可以分解为以下几个步骤: (1) 将A上的n-1个圆盘,借助C,从A移到B上; (2) 把A上第n个圆盘,直接从A移到C上; (3) 将B上的n-1个圆盘,借助A,从B移到C上。
递归方式实现的汉诺塔(Java版):
public class Hanoi {
// 阶数
private static int n = 4;
//验证汉诺塔移动次数
private static int sum=0;
public static void main(String[] args) {
System.out.println(String.format("%s层汉诺塔的移动顺序:", n));
move(n, 'A','B','C');
System.out.println("汉诺塔移动次数:"+sum);
}
/**
* (n-1) A -> B
* n A -> C
* (n-1) B -> C
*
* 结束条件为:当n=1 时, A -> C
*/
public static void move(int n,char A, char B, char C) {
if(n==1) {
System.out.println(A + " -> " + C);
sum++;
}
else {
move(n-1, A, C, B);//每次都是输出A->C,所以要看到A->B,就需要将B和C交换
if(n==Hanoi.n)
System.out.println("前面完成(n-1)层:从A移动到B");
System.out.println(A + " -> " + C);
sum++;
if(n==Hanoi.n)
System.out.println("完成第(n)层:从A移动到C");
move(n-1, B, A, C);//每次都是输出A->C,所以要看到B->C,就需要将A和B交换
if(n==Hanoi.n)
System.out.println("前面完成(n-1)层:从B移动到C");
}
}
}
执行结果:
3层汉诺塔的移动顺序:
A -> C
A -> B
C -> B
前面完成(n-1)层:从A移动到B
A -> C
完成第(n)层:从A移动到C
B -> A
B -> C
A -> C
前面完成(n-1)层:从B移动到C
汉诺塔移动次数:7
先完成(n-1)层:从A移动到B,
再完成第(n)层:从A移动到C,
最后完成(n-1)层:从B移动到C。
通过数学推导汉诺塔移动次数
递归算法可以通过递归式的方式去推导证明,现在通过递归式推导汉诺塔移动次数。
假定n是盘子的数量,T(n)是移动n个圆盘的移动次数。
当n=1时,T(1)=1
当n=2时,T(2)=2T(1)+1
当n=3时,T(3)=2T(2)+1
得汉诺塔递归式:
由递归式求n阶汉诺塔移动次数:
由递归式可知:
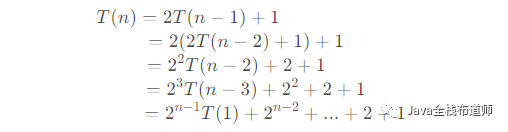
又因当n=1时,T(1)=1,得:
解得n阶汉诺塔移动次数为: 次。
汉诺塔与二进制
公式
这就像是n位二进制的和,最终得到n位二进制的最大值(全1)
所以有,n阶汉诺塔移动次数等于n位二进制得最大值,如:4阶汉诺塔移动次数为
每个盘子的移动次数,观察下图:
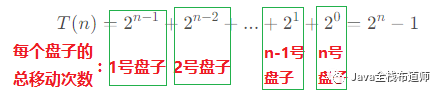
如图可知,每个盘子移动总次数刚好相反,
所以,n阶汉诺塔的第i个盘子总的移动次数为:
3阶汉诺塔图解与二进制关系
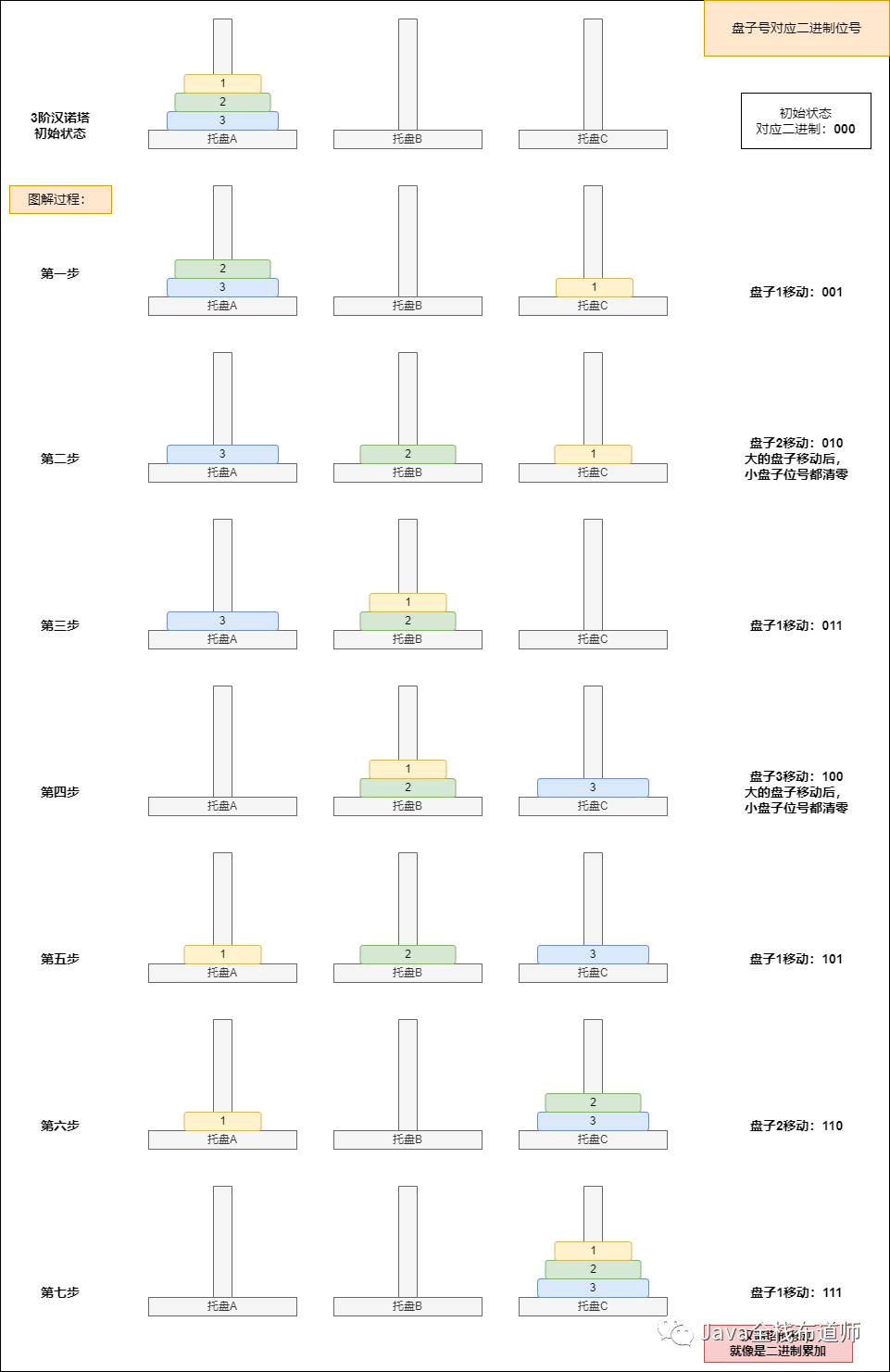
汉诺塔与满二叉树
递归算法会有相对应的递归树,而汉诺塔的递归树刚好是满二叉树,即所有分支结点都有两个叶子结点。
调整汉诺塔对算法代码的输出信息后:
public class Hanoi {
// 阶数
private static int n = 3;
public static void main(String[] args) {
System.out.println(String.format("%s层汉诺塔的移动顺序:", n));
int sum = moveTree(n, 'A','B','C');
System.out.println("汉诺塔移动次数:"+sum);
}
/**
* 汉诺塔与满二叉树
* (n-1) A -> B
* n A -> C
* (n-1) B -> C
*
* 结束条件为:当n=1 时, A -> C
*/
public static int moveTree(int n,char A, char B, char C) {
if(n==1)
System.out.println(String.format("第 %s 层(叶子节点):%s -> %s",n, A, C));
else {
moveTree(n-1, A, C, B);//每次都是输出A->C,所以要看到A->B,就需要将B和C交换
if(n==Hanoi.n)
System.out.println(String.format("第 %s 层(根节点):%s -> %s", n, A, C));
else
System.out.println(String.format("第 %s 层(分支结点):%s -> %s", n, A, C));
moveTree(n-1, B, A, C);//每次都是输出A->C,所以要看到B->C,就需要将A和B交换
}
//汉诺塔的移动次数为: 2^n-1
return (int) Math.pow(2, n)-1;
}
}
3层汉诺塔的移动顺序:
第 1 层(叶子节点):A -> C
第 2 层(分支结点):A -> B
第 1 层(叶子节点):C -> B
第 3 层(根节点):A -> C
第 1 层(叶子节点):B -> A
第 2 层(分支结点):B -> C
第 1 层(叶子节点):A -> C
汉诺塔移动次数:7
3阶汉诺塔对应的满二叉树:
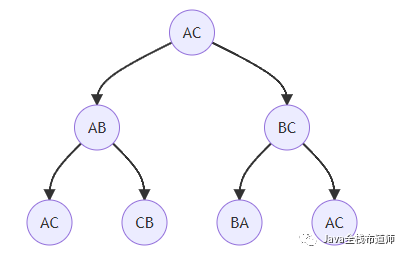
3阶汉诺塔的移动步骤为满二叉树的中序遍历:AC、AB、CB、AC、BA、BC、AC
从输出结果可以看到,汉诺塔盘子编号对应满二叉树自底向上计算的层号,如:1号盘子的移动对应是叶子节点,最底层盘子对应根节点。
为了更好理解,可以写成这样:
public static int moveTree(int n,char A, char B, char C) {
if(n==1)
System.out.println(String.format("第 %s 层(叶子节点):%s -> %s",Hanoi.n-n+1, A, C));
else {
moveTree(n-1, A, C, B);//每次都是输出A->C,所以要看到A->B,就需要将B和C交换
if(n==Hanoi.n)
System.out.println(String.format("第 %s 层(根节点):%s -> %s", Hanoi.n-n+1, A, C));
else
System.out.println(String.format("第 %s 层(根节点):%s -> %s", Hanoi.n-n+1, A, C));
moveTree(n-1, B, A, C);//每次都是输出A->C,所以要看到B->C,就需要将A和B交换
}
//汉诺塔的移动次数为: 2^n-1
return (int) Math.pow(2, n)-1;
}
汉诺塔递归实现与二叉树中序遍历的递归实现,在代码实现上很类似
public static void inorder(TreeNode root) {
if (root == null)
return;
inorder(root.left);
System.out.print(root.val);
inorder(root.right);
}
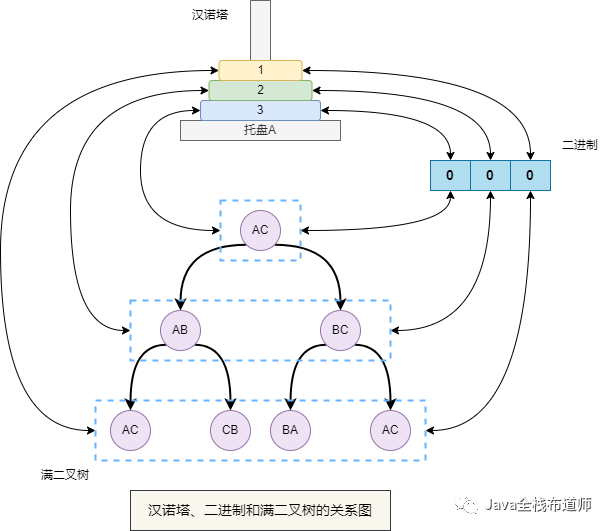
汉诺塔的移动步骤可以用满二叉树的中序遍历来表示,反过来,我们可以通过满二叉树的特性推导出汉诺塔的一些特性:
-
满二叉树总的结点数为,所以汉诺塔移动次数为;
-
满二叉树第n层的节点数为,所以n阶汉诺塔第i个盘子被移动的次数为;
-
满二叉树叶子节点数为,所以汉诺塔第一个盘子被移动的次数为;
-
满二叉树是二进制的一种表现形式,所以汉诺塔也是二进制的一种表现形式,其中汉诺塔的移动过程就是二进制的累加过程。
最后附上三者的关系图
总结
如果这些结论都是自己推导发现的话,你会发现充满惊喜。其推导过程非常有意思,好像冥冥之中万物都和二进制相关。文章想表达的不仅仅是得出汉诺塔有哪些特性,更重要的是希望能在学习中,发现学习本身的乐趣,从而滋养内在的好奇心、探索精神,不断地自我推进,让学习越来越有趣越有动力。