Models for Human-Like Tasks 

类似人类任务的模型

The example we gave above involves making a model for numerical data that essentially comes from simple physics—where we’ve known for several centuries that “simple mathematics applies”. But for ChatGPT we have to make a model of human-language text of the kind produced by a human brain. And for something like that we don’t (at least yet) have anything like “simple mathematics”. So what might a model of it be like?

我们上面给出的例子涉及到为数值数据建立一个模型，这些数据基本上来自于简单的物理学——几个世纪以来我们一直知道“简单的数学适用”。但对于 ChatGPT，我们必须建立一个人类大脑产生的人类语言文本的模型。对于这样的任务，我们（至少目前）没有任何类似于“简单的数学”。那么它的模型可能是什么样子的？

Before we talk about language, let’s talk about another human-like task: recognizing images. And as a simple example of this, let’s consider images of digits (and, yes, this is a classic machine learning example):

在我们讨论语言之前，让我们来谈谈另一个类似于人类的任务：图像识别。作为这方面的一个简单示例，我们考虑一下数字的图像（是的，这是一个经典的机器学习示例）：

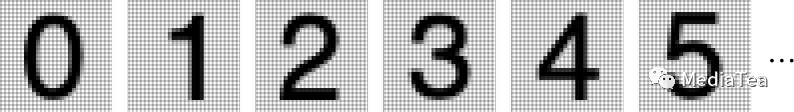
One thing we could do is get a bunch of sample images for each digit:

我们可以做的一件事是为每个数字获取一批样本图像：

Then to find out if an image we’re given as input corresponds to a particular digit we could just do an explicit pixel-by-pixel comparison with the samples we have. But as humans we certainly seem to do something better—because we can still recognize digits, even when they’re for example handwritten, and have all sorts of modifications and distortions:

然后，为了确定给定输入图像是否对应于特定数字，我们可以将其与我们拥有的样本进行像素对比。但是作为人类，我们肯定在做得更好——因为我们仍然可以识别数字，即使它们是手写的，还有各种修改和扭曲：

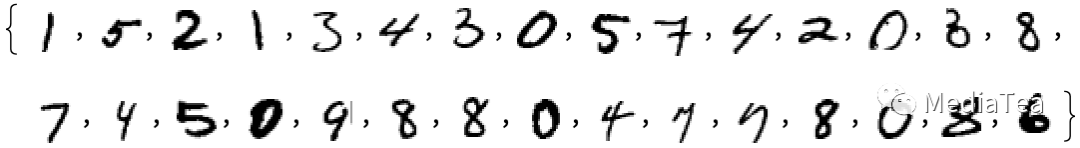
When we made a model for our numerical data above, we were able to take a numerical value x that we were given, and just compute a + b x for particular a and b. So if we treat the gray-level value of each pixel here as some variable xi is there some function of all those variables that—when evaluated—tells us what digit the image is of? It turns out that it’s possible to construct such a function. Not surprisingly, it’s not particularly simple, though. And a typical example might involve perhaps half a million mathematical operations.

当我们为上面的数值数据建立模型时，我们能够将给定的数值 x，并计算特定的 a 和 b 的 a + b x。因此，如果我们将每个像素的灰度值视为某些变量 xi，则是否存在某个涉及所有这些变量的函数，当我们进行评估时，告诉我们图像是哪个数字的？事实证明，是可能构造出这样的函数的。毫不奇怪，这并不特别简单。而一个典型的示例可能涉及大约五十万次数学运算。

But the end result is that if we feed the collection of pixel values for an image into this function, out will come the number specifying which digit we have an image of. Later, we’ll talk about how such a function can be constructed, and the idea of neural nets. But for now let’s treat the function as black box, where we feed in images of, say, handwritten digits (as arrays of pixel values) and we get out the numbers these correspond to:

但最终的结果是，如果我们将图像的像素值集合输入到这个函数中，输出的结果将是指定我们所拥有的图像的数字。稍后，我们将讨论如何构建这样的函数，以及神经网络的概念。但现在让我们将这个函数视为黑盒子，我们将手写数字的图像（作为像素值数组）输入，然后得到对应的数字：

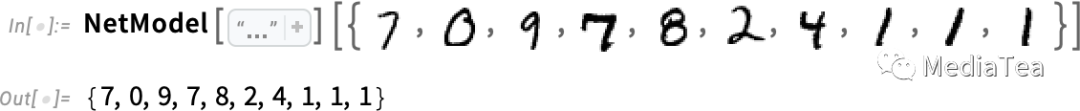
But what’s really going on here? Let’s say we progressively blur a digit. For a little while our function still “recognizes” it, here as a “2”. But soon it “loses it”, and starts giving the “wrong” result:

但是这里真正发生了什么？假设我们逐渐模糊一个数字。一开始，我们的函数仍然“识别”它，比如“2”。但很快它就“失去了识别”，并开始给出“错误”的结果：

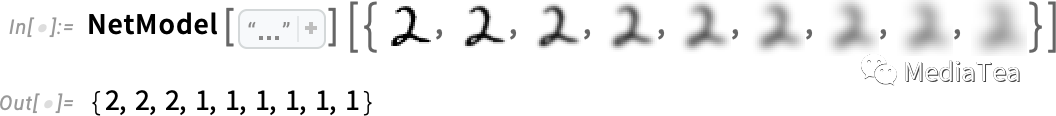
But why do we say it’s the “wrong” result? In this case, we know we got all the images by blurring a “2”. But if our goal is to produce a model of what humans can do in recognizing images, the real question to ask is what a human would have done if presented with one of those blurred images, without knowing where it came from.

但我们为什么说这是“错误”的结果？在这种情况下，我们知道我们得到的所有图像都是通过模糊“2”而获得的。但是，如果我们的目标是为人类在识别图像方面的能力建立一个模型，那么真正需要问的问题是：如果人类被呈现了这些模糊的图像，而不知道它们来自哪里，他们会做什么？

And we have a “good model” if the results we get from our function typically agree with what a human would say. And the nontrivial scientific fact is that for an image-recognition task like this we now basically know how to construct functions that do this.

如果我们的函数产生的结果通常与人类的判断相符，那么我们就拥有了一个“好的模型”。而这个重要的科学事实是，在像这样的图像识别任务中，我们现在基本上知道如何构建能够实现这一点的函数。

Can we “mathematically prove” that they work? Well, no. Because to do that we’d have to have a mathematical theory of what we humans are doing. Take the “2” image and change a few pixels. We might imagine that with only a few pixels “out of place” we should still consider the image a “2”. But how far should that go? It’s a question of human visual perception. And, yes, the answer would no doubt be different for bees or octopuses—and potentially utterly different for putative aliens.

我们是否可以“数学上证明”它们有效？嗯，不行。因为为此我们必须对人类的所作所为拥有一个数学理论。拿“2”的图像并改变几个像素。我们可以想象，只有几个像素“有点偏离”，我们仍然应该将图像视为“2”。但是应该偏离多远？这是一个关于人类视觉感知的问题。是的，对于蜜蜂或章鱼，答案无疑会不同——对于假定的外星人来说可能完全不同。

“点赞有美意，赞赏是鼓励”