【LetMeFly】2050.并行课程 III：DFS

力扣题目链接：https://leetcode.cn/problems/parallel-courses-iii/

给你一个整数 n ，表示有 n 节课，课程编号从 1 到 n 。同时给你一个二维整数数组 relations ，其中 relations[j] = [prevCourse_j, nextCourse_j] ，表示课程 prevCourse_j 必须在课程 nextCourse_j 之前完成（先修课的关系）。同时给你一个下标从 0 开始的整数数组 time ，其中 time[i] 表示完成第 (i+1) 门课程需要花费的月份数。

请你根据以下规则算出完成所有课程所需要的最少月份数：

如果一门课的所有先修课都已经完成，你可以在任意时间开始这门课程。
你可以同时上 任意门课程 。

请你返回完成所有课程所需要的最少月份数。

注意：测试数据保证一定可以完成所有课程（也就是先修课的关系构成一个有向无环图）。

示例 1:

输入：n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出：8
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月，课程 2 花费 2 个月。
所以，最早开始课程 3 的时间是月份 3 ，完成所有课程所需时间为 3 + 5 = 8 个月。

示例 2：

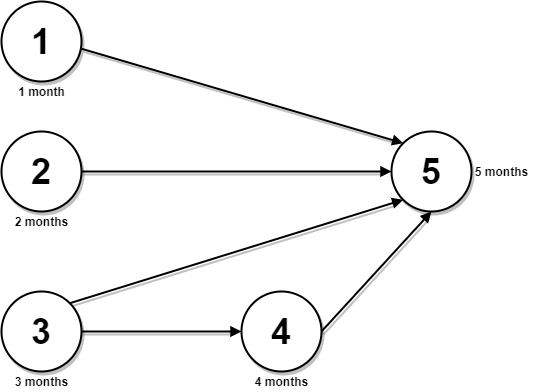
输入：n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出：12
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ，2 和 3 。
在月份 1，2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始，也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1，2，3 和 4 之后开始，也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。

提示：

1 <= n <= 5 * 10⁴
0 <= relations.length <= min(n * (n - 1) / 2, 5 * 10⁴)
relations[j].length == 2
1 <= prevCourse_j, nextCourse_j <= n
prevCourse_j != nextCourse_j
所有的先修课程对 [prevCourse_j, nextCourse_j] 都是 互不相同 的。
time.length == n
1 <= time[i] <= 10⁴
先修课程图是一个有向无环图。

方法一：深度优先搜索（DFS）

这道题其实不难，无脑记忆化搜索就可以了。

首先建立一个邻接表pre，pre[i]记录课程i的所有先修课程，接着写一个函数dfs(n)，用来求课程n最早修完的日期。

公式： $课程 i 的最早完成时 = ma x (其先修课的最早完成时) + 课程 i 耗时$

int dfs(n) {
    若已计算过n则直接返回

    int ans = 0;
    for (int thisPre : pre[n]) {
		ans = max(ans, dfs(thisPre));
	}
	ans += time[n];
	return ans;  // 返回并“记忆之”
}

时间复杂度 $O (n + l e n (re l a t i o n s))$
空间复杂度 $O (n + l e n (re l a t i o n s))$

AC代码

Python

# from typing import List
# from functools import cache

class Solution:
    @cache
    def dfs(self, n):
        if self.dp[n]:
            return self.dp[n]
        for thisPre in self.pre[n]:
            self.dp[n] = max(self.dp[n], self.dfs(thisPre))
        self.dp[n] += self.time[n]
        return self.dp[n]

    def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:
        self.time = time
        self.dp = [0] * n
        self.pre = [[] for _ in range(n)]  # 这里不能写成[[]] * n！！！
        for thisPre, thisNext in relations:
            self.pre[thisNext - 1].append(thisPre - 1)
        return max(self.dfs(i) for i in range(n))

C++

class Solution {
private:
    vector<vector<int>> pre;
    vector<int> dp;
    vector<int> time;

    int dfs(int n) {  // n从0开始
        if (dp[n]) {
            return dp[n];
        }
        for (int thisPre : pre[n]) {
            // printf("n = %d, thisPre = %d, max(%d", n, thisPre, dp[n]);  //******
            dp[n] = max(dp[n], dfs(thisPre));
            // printf(", %d) = %d\n", dfs(thisPre), dp[n]);  //*********
        }
        return (dp[n] += time[n]);
    }
public:
    int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
        this->time = time;
        pre.resize(n);
        dp.resize(n);
        for (vector<int>& relation : relations) {
            pre[relation[1] - 1].push_back(relation[0] - 1);
        }

        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans = max(ans, dfs(i));
        }
        return ans;
    }
};