机器学习

概述

以分类任务为例，机器学习可以看作是找一个猫狗的分类函数。

• step1: 设计未知函数；其中，权重和偏置都是神经元中位置参数（可学习的）；
• step2: 定义损失函数；
• step3：训练优化参数；

Meta Learning

模型训练与优化

  原学习同样是学习一个函数，该函数的输入是图像数据，输出还是一个函数，如输出一个分类器。原学习的损失在计算时包含多个任务，每个任务都有训练集和测试集。
  对于其中的一个任务，下图是一个很清晰的例子。

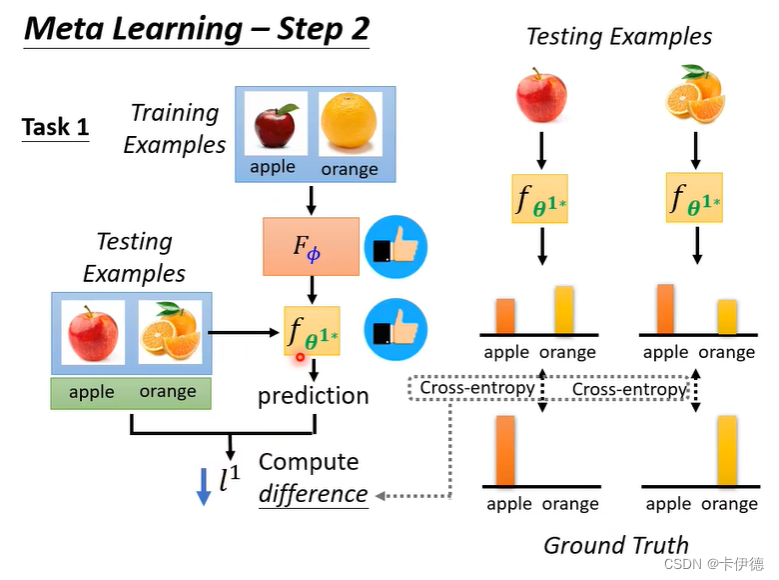
  现在解释这张图。对于任务1（Task 1）而言，他的训练集是苹果和橘子，$F_{\theta }$ 就是原学习训练的目标函数，它的输入是图片，输出是分类器$f_{\theta }^{\ast }$ 。 $f_{\theta }^{\ast }$ 就是一个分类苹果和橘子的分类器，如果$f_{\theta }^{\ast }$ 模型精度高，则说明$F_{\theta }$ 好。因此，在训练过程中，将测试数据输入$f_{\theta }^{\ast }$，进行测试，并计算损失$l^1$。这个损失就是普通深度学习的计算方法（上图右边）。 该损失越大，说明$f_{\theta }^{\ast }$ 越差，即就是$F_{\theta }$越差。
对于其他多个任务，计算也是如此。因此最终的损失为：
$L(\theta )={\sum }_{n=0}^N{l}^n$
  从上面的过程就能看出，元学习与机器学习的区别之一就是元学习在训练过程中同时包含训练数据集和测试数据集。
  下一步就是利用最小化损失函数来求最佳参数${\theta }^{\ast }$。即：
$${\theta }^{\ast }=argminL(\theta )$$

模型测试

  在训练得到一个已经学习了的学习模型${\theta }^{\ast }$。该模型拥有学习能力，则进入测试阶段。
如图所示：

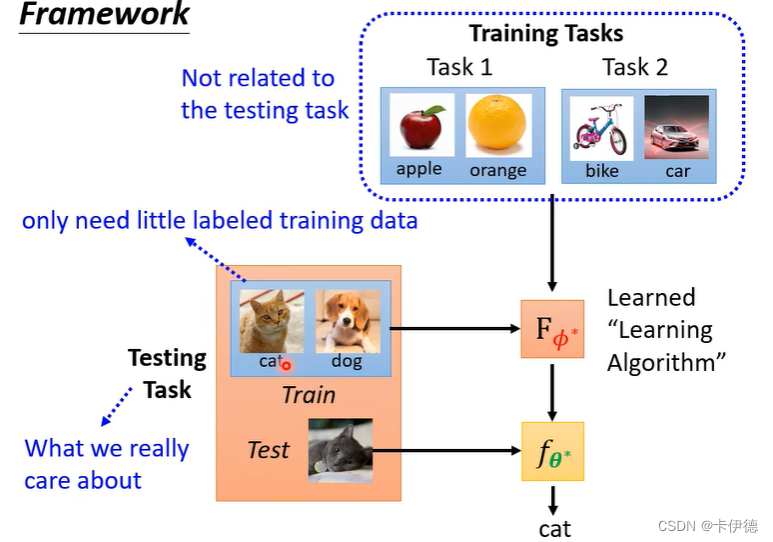
  在测试阶段，就是元学习的精髓了。在测试阶段，首先将训练数据猫和狗（训练阶段没有见过的类型）输入$f_{\theta }^{\ast }$ ，和训练阶段一样，输出一个分类模型$F_{\theta }$。这等于是给模型给了一丢丢他没见过的类型的数据和标签，让它简单学习一下（它有学习能力）。然后，再输入测试数据（和测试阶段的训练数据类型一样），让该模型进行预测。
  这个过程说明了一个问题，模型具有学习能力。比如说一个人生下来啥也没见过，如果给他给十张猫和狗的图片，并给他说哪张是猫，哪张是狗，并给他测试几张猫和狗的照片，这个过程就让他有一个学会分类的能力，也就是训练阶段（包含训练数据和测试数据）。在测试阶段，给他两张鸡和鸦的照片，并说明哪张是鸡和哪张是鸦，然后，给他一张（少样本few-shot）新的测试照片，让他进行分类，他就能够正确分类（也包含训练数据和测试数据，但是该数据是一个全新类别，而不是训练阶段同样的类别，这也是和监督学习的区别，监督学习是训练集给一万张猫，学会猫长什么样，完了给一张新的猫的照片，让测试）。

本文参考 李宏毅老师的B站课程。