文章目录

【LeetCode热题100】打卡第44天：倒数第30~25题
- ⛅前言
移动零
- 🔒题目
- 🔑题解
寻找重复数
- 🔒题目
- 🔑题解
二叉树的序列化与反序列化
- 🔒题目
- 🔑题解
最长递增子序列
- 🔒题目
- 🔑题解
删除无效括号
- 🔒题目
- 🔑题解

【LeetCode热题100】打卡第44天：倒数第30~25题

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

博客主页💖：知识汲取者的博客

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

移动零

🔒题目

原题链接：283.移动零

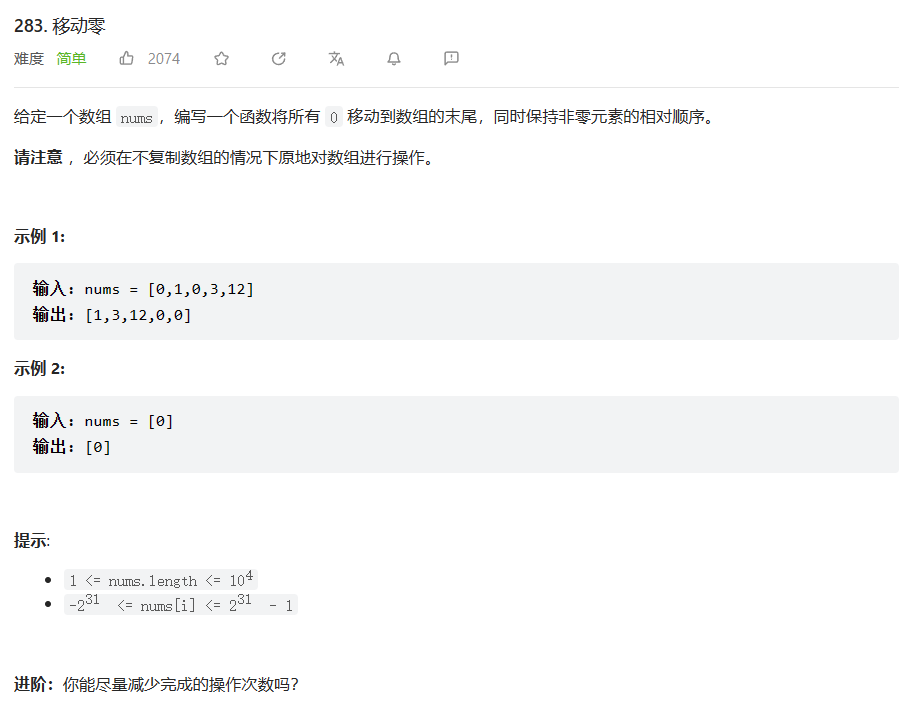
🔑题解

解法一：暴力枚举即可

但是我们使用copyOfRange方法存在一个弊端，它会重现创建一个数组，然后将值赋值给新的数组引用，给不是在原有的数组引用上进行赋值，所以这里就导致最终无法修改到我们要实现效果的数组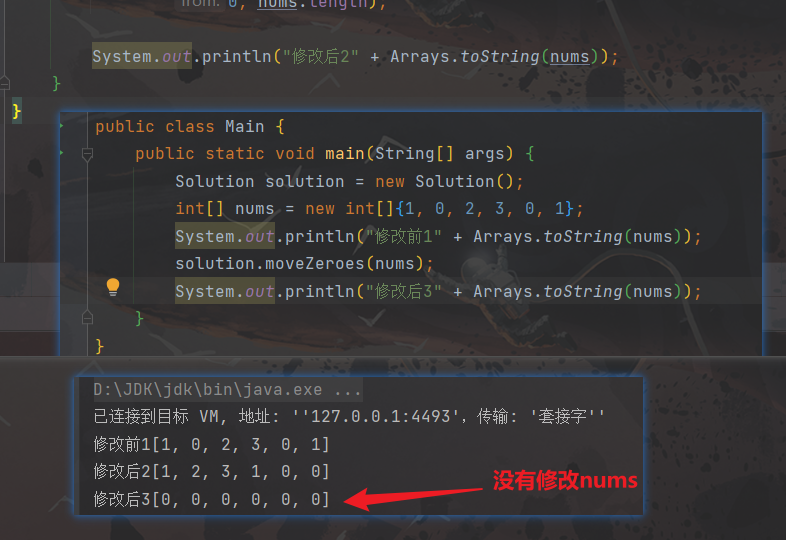

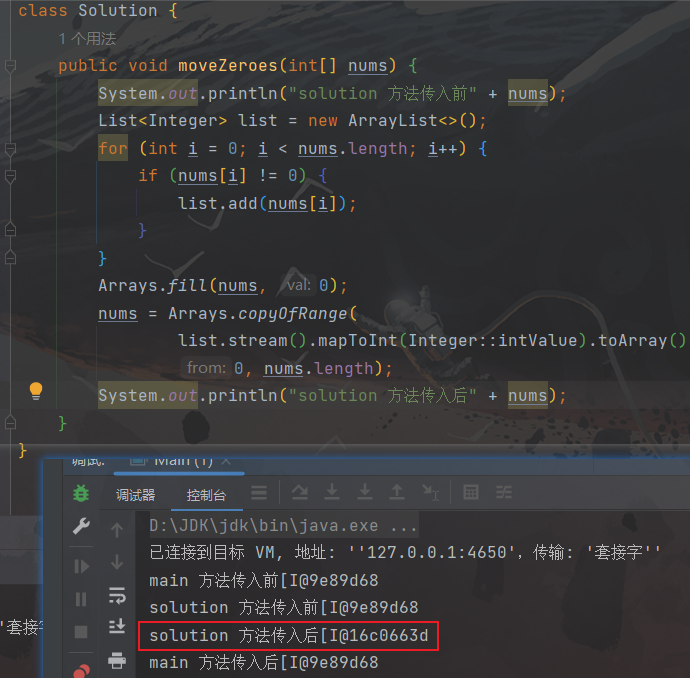
下方代码，最终输出的nums全部是 0

/**
 * @author ghp
 * @title
 * @description
 */
class Solution {
    public void moveZeroes(int[] nums) {
        List<Integer> list = new ArrayList<>();
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0){
                list.add(nums[i]);
            }
        }
        Arrays.fill(nums, 0);
        nums =  Arrays.copyOfRange(
                list.stream().mapToInt(Integer::intValue).toArray(),
                0, nums.length);
    }
}

复杂度分析：

时间复杂度： $O (n)$
空间复杂度： $O (n)$

其中 $n$ 为数组中元素的个数

解决方法：使用for循环，逐个赋值（这里我就是使用lambda表达式实现，效果都是一样的，但是这种更加优雅）

/**
 * @author ghp
 * @title
 * @description
 */
class Solution {
    public void moveZeroes(int[] nums) {
        List<Integer> list = new ArrayList<>();
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) {
                list.add(nums[i]);
            }
        }
        Arrays.fill(nums, 0);
        IntStream.range(0, list.size())
                .forEach(i -> nums[i] = list.get(i));
    }
}

解法二：双指针

这个思路是非类似于快排的那个划分左右区间，设置两个指针，使得左区间都比主元小，右区间都比主元大或等。

这里我们相当于是把0当作主元，左区间都是不等于0的，右区间都是等于0的
```
class Solution {
    public void moveZeroes(int[] nums) {
        int i = 0;
        // 遍历数组，将非0元素放到i的左侧
        for (int j = 0; j < nums.length; j++) {
            if (nums[j] != 0){
                // 当前元素不等于0，将非0元素放到i的左侧
                int t = nums[j];
                nums[j] = nums[i];
                nums[i] = t;
                i++;
            }
        }
    }
}
```
复杂度分析：
- 时间复杂度： $O (n)$
- 空间复杂度： $O (1)$
其中 $n$ 为数组中元素的个数

寻找重复数

🔒题目

原题链接：287.寻找重复数

🔑题解

本题总共有以下解法：

需要额外空间，需要修改原始数组：排序
需要额外空间，不需要修改原始数组：计数法、哈希表
不需要额外空间，需要修改原始数组：标记法、索引排序
不需要额外空间，不需要修改原始数组：暴力枚举、二分查找、位运算、快慢指针

PS：本文只讲解了二分查找、快慢指针、位运算三种能过且比较牛的方法，关于其它方法感兴趣都可以参考这篇文章：9种方法（可能是目前最全的），拓展大家思路 - 寻找重复数 - 力扣（LeetCode）

解法一：快慢指针（Floyd 判圈算法）

这个算法在前面已经多次遇到了，比如：第33天的环形链表、第34天的排序链表、第35天的相交链表、第40天的回文链表等都能看到快慢指针算法的身影。可能我们一下子无法直接联想到环形链表，这里我们画一个草图，将数组转换成一个环形链表（这是一种数学抽象，类似于七桥问题，把一个问题抽象成另一个与之等价的问题）

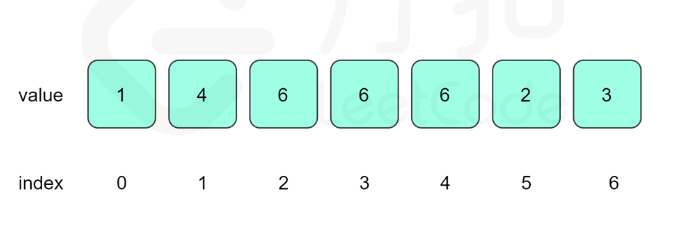
我们把数值的值当成链表的下一个节点，这个值与索引进行一个映射，从而可以通过上面的链表得到下面这个链表，此时我们把”要数组中的找重复元素“这个问题转换成"要找链表中环的入口节点"，说到这里，如果你对环形链表这一题有经验的话，很快就能够解决了。如果你对环形链表不是很懂的话，可以参考这篇文章【LeetCode热题100】打卡第33天：环形链表

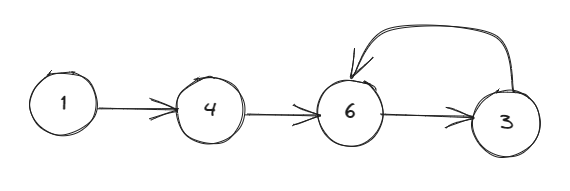
注意：本题能够使用快慢指针的前提是 $1 <= n u m s [i] <= n$ ，这样能够保障指针无论如何移动都不会出现索引越界

这里初略讲解以下如何定位环形链表的入环节点：
1. 第一次遍历，fast比slow多走一步，寻找到fast和slow相等的节点，然后将fast重置到起始节点
2. 第二次遍历，fast和slow走相同的步数，寻找到fast和slow相等的节点，此时fast和slow相遇的节点就是入环节点
至于详细证明思路，可以参考我上面给出的那个链接，链接的那篇文章中已给出比较详细的解答了
```
/**
 * @author ghp
 * @title
 * @description
 */
class Solution {
    public int findDuplicate(int[] nums) {
        int fast = 0, slow = 0;
        do {
            fast = nums[nums[fast]];
            slow = nums[slow];
        } while (fast != slow);
        fast = 0;
        while (fast != slow) {
            fast = nums[fast];
            slow = nums[slow];
        }
        return fast;
    }
}
```
复杂度分析：
- 时间复杂度： $O (n)$
- 空间复杂度： $O (1)$
其中n为数组中元素的个数
解法二：二分查找

本题主要用到了抽屉原理，简单来说就是把 10 个苹果放进 9 个抽屉，至少有一个抽屉里至少放 2 个苹果。

其此我们还需要寻找出有序的地方，本题有序的地方是隐式的，即比当前元素小的元素是有序的，只要发现这一点，其实就会变得很简单，但往往这一点一般很慢发现，这也是本题相较于其他显示有序的一个难点

我们新增一个变量cnt[i]来记录当前数组中小于等于i的数有多少个，然后可以的发现cnt数组是有序的，对于有序数组我们

①如果我们将n个数放到n个位置上（数的范围是1~n），这些数不重复，则此时 cnt==mid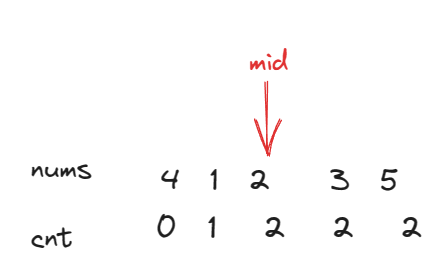

②如果我们将n个数放到n+1个位置上（数的范围是1~n），这些数不重复，如果此时 cnt<=mid，则说明重复的数一定在左侧区间，因为数是在1~n这个区间选的，cnt[n]<=mid说明比n小的数不到一半（正常情况是刚好一半的），根据抽屉原理，一定是有一个比mid小的数重复了，这样才会出现cnt[n]<=mid，所以重复的数在mid的左侧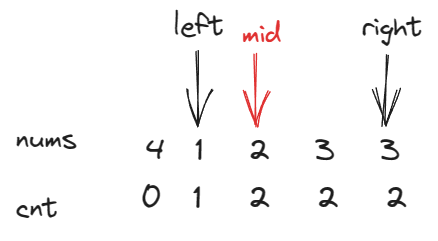

③如果我们将n个数放到n+1个位置上，如果是左侧的数多了，则会导致cnt[n]>mid，此时我们可以在左侧区间寻找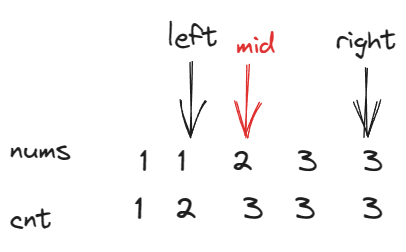

温馨提示：对于所有的二分查找，边界值都是需要十分注意的，这个我在以前总结的二分查找中就已经进行了详细讲解，这里我也不在赘述了，直接给出结论，如果想要了解的，可以参考我以前写的一篇关于二分查找边界值问题的总结
1. 对于向下取整mid = (right-left)/2 + left ，如果取等 while(left<=right)，那么目标值在右right=mid-1，目标值在左left=mid+1
2. 对于向下取整mid=(right-left)/2 + left，如果不取等while(left<right)，那么目标值在右right=mid，目标值在左left=mid+1
  
  如果取等匹配right=mid会导致死循环，如果不取等匹配right=mid-1会出现遗漏导致结果错误
```
/**
 * @author ghp
 * @title
 * @description
 */
class Solution {
    public int findDuplicate(int[] nums) {
        int left = 1, right = nums.length - 1;
        while (left < right) {
            int mid = (right - left) / 2 + left;
            // 计算当前小于等于mid的元素有多少个
            int count = 0;
            for (int i = 0; i < nums.length; i++) {
                if (nums[i] <= mid){
                    count++;
                }
            }
            if (count > mid){
                // 比mid小的元素超过了mid个，根据抽屉原理可以知道mid左侧出现了重复元素
                right = mid;
            }else{
                // 比mid小的元素超过了mid个，根据抽屉原理可以知道mid右侧出现了重复元素
                left = mid + 1;
            }
        }
        return left;
    }
}
```
复杂度分析：
- 时间复杂度： $O (n l o g n)$
- 空间复杂度： $O (1)$
其中n为数组中元素的个数

解法三：位运算

太强了，感兴趣的可以去看LeetCode官网，我先把前面两种解法消化吸收了

class Solution {
    public int findDuplicate(int[] nums) {
        int n = nums.length, ans = 0;
        int bit_max = 31;
        while (((n - 1) >> bit_max) == 0) {
            bit_max -= 1;
        }
        for (int bit = 0; bit <= bit_max; ++bit) {
            int x = 0, y = 0;
            for (int i = 0; i < n; ++i) {
                if ((nums[i] & (1 << bit)) != 0) {
                    x += 1;
                }
                if (i >= 1 && ((i & (1 << bit)) != 0)) {
                    y += 1;
                }
            }
            if (x > y) {
                ans |= 1 << bit;
            }
        }
        return ans;
    }
}

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/find-the-duplicate-number/solution/xun-zhao-zhong-fu-shu-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析：

时间复杂度： $O (n l o g n)$
空间复杂度： $O (1)$

其中n为数组中元素的个数

二叉树的序列化与反序列化

🔒题目

原题链接：297.二叉树的序列化与反序列化

🔑题解

解法一：BFS（层序遍历）

不知道为什么我第一眼看着提感觉挺简单的，直接BFS不就好了吗，结果bug频出，一眨眼一小时就过去了，经过不断的debug最终成功完成了初步代码，并最终过了😄写这题的思路也比较简答，直接使用BFS实现层序遍历即可

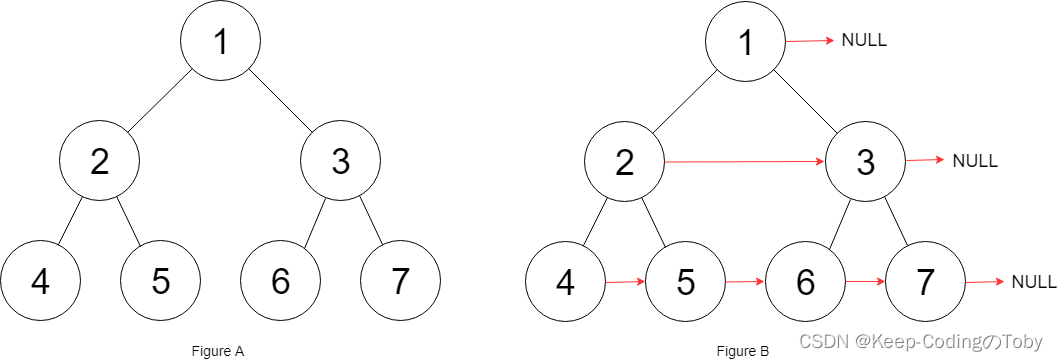
如果不会层序遍历的话，可以参考这篇文章：【LeetCode热题100】打卡第29天：二叉树的层序遍历

class Codec {
    public String serialize(TreeNode root) {
        if (root == null) {
            // 防止NPE
            return null;
        }
        // 存储每一层的节点的值
        StringBuilder ans = new StringBuilder(root.val + ",");
        // BFS层序遍历所有节点，将二叉树所有节点的值转存到ans中
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode pre = queue.poll();
            TreeNode left = pre.left;
            if (left != null) {
                queue.offer(left);
            }
            ans.append(left == null ? "null" : left.val).append(",");
            TreeNode right = pre.right;
            if (right != null) {
                queue.offer(right);
            }
            ans.append(right == null ? "null" : right.val).append(",");
        }
        // 删除最后一个多余的逗号
        ans.deleteCharAt(ans.length() - 1);
        return ans.toString();
    }

    public TreeNode deserialize(String data) {
        if (data == null) {
            // 防止NPE
            return null;
        }
        // 将String转成List方便后续逻辑处理
        String[] dataStr = data.split(",");
        List<Integer> dataList = Arrays.stream(dataStr)
                .map(str -> str.equals("null") ? null : Integer.valueOf(str))
                .collect(Collectors.toList());
        // BFS层序遍历所有节点，将层序遍历的字符串重新构建成一棵二叉树
        Deque<TreeNode> queue = new LinkedList<>();
        // 将根节点加入队列中
        TreeNode root = new TreeNode(dataList.get(0));
        queue.offer(root);
        dataList.remove(0);
        while (!dataList.isEmpty()) {
            TreeNode node = queue.poll();
            if (dataList.get(0) != null) {
                // 这里一定要判空，否则自动拆箱时会报NPE，下面那个判空也是一样的
                node.left = new TreeNode(dataList.get(0));
                queue.offer(node.left);
            }
            dataList.remove(0);
            if (dataList.isEmpty()) {
                // 防止NPE
                break;
            }
            if (dataList.get(0) != null) {
                node.right = new TreeNode(dataList.get(0));
                queue.offer(node.right);
            }
            dataList.remove(0);
        }
        return root;
    }
}

复杂度分析：

序列化

时间复杂度： $O (n)$
空间复杂度： $O (n)$

反序列化

时间复杂度： $O (n)$
空间复杂度： $O (n)$

其中 $n$ 为二叉树节点的个数

代码优化：

对于serialize方法：

每个循环只需要处理一个节点，不需要额外的变量来保存父节点

对于deserialize方法：

使用整型数组代替列表，因为在循环中频繁进行插入和删除操作会导致列表的性能下降
使用索引标记当前节点的位置，避免频繁调用 dataList.get() 方法

/**
 * @author ghp
 * @title
 * @description
 */
class Codec {

    public String serialize(TreeNode root) {
        if (root == null) {
            return null;
        }
        StringBuilder ans = new StringBuilder();
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (node != null) {
                ans.append(node.val).append(",");
                queue.offer(node.left);
                queue.offer(node.right);
            } else {
                ans.append("null,");
            }
        }
        ans.deleteCharAt(ans.length() - 1);
        return ans.toString();
    }

    public TreeNode deserialize(String data) {
        if (data == null) {
            return null;
        }
        String[] dataStr = data.split(",");
        List<Integer> dataList = Arrays.stream(dataStr)
                .map(str -> str.equals("null") ? null : Integer.valueOf(str))
                .collect(Collectors.toList());
        Deque<TreeNode> queue = new LinkedList<>();
        TreeNode root = new TreeNode(dataList.get(0));
        queue.offer(root);
        int index = 1;
        for (; index < dataList.size(); index += 2) {
            TreeNode node = queue.poll();
            if (dataList.get(index) != null) {
                node.left = new TreeNode(dataList.get(index));
                queue.offer(node.left);
            }
            if (index + 1 < dataList.size() && dataList.get(index + 1) != null) {
                node.right = new TreeNode(dataList.get(index + 1));
                queue.offer(node.right);
            }
        }
        return root;
    }
}

解法二：DFS（前序遍历）

这里主要是通过前序遍历实现

序列化实现比较简单，直接DFS搜索即可： [1,2,null,null,3,4,null,null,5,null,null]
反序列化的时候，第一个元素为根节点，接下来都是按照前序遍历的顺序，先走左边，直到遇到 null 结束，然后换另一边

整个过程递归进行

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}

/**
 * @author ghp
 * @title
 * @description
 */
class Codec {

    public String serialize(TreeNode root) {
        StringBuilder ans = new StringBuilder();
        dfs(root, ans);
        ans.deleteCharAt(ans.length() - 1);
        return ans.toString();
    }

    private void dfs(TreeNode root, StringBuilder ans) {
        if (root == null) {
            ans.append("null,");
            return;
        }
        ans.append(root.val).append(",");
        dfs(root.left, ans);
        dfs(root.right, ans);
    }

    public TreeNode deserialize(String data) {
        String[] dataStr = data.split(",");
        // 根据前序遍历的结果构建二叉树
        return buildTree(dataStr);
    }

    private int i = 0;
    private TreeNode buildTree(String[] dataStr) {
        String value = dataStr[i++];
        if (value.equals("null")) {
            // 防止自动拆箱导致NPE，同时也是递归结束条件
            return null;
        }
        TreeNode node = new TreeNode(Integer.valueOf(value));
        // 构建左子树
        node.left = buildTree(dataStr);
        // 构建右子树
        node.right = buildTree(dataStr);
        return node;
    }
}

复杂度分析：

序列化

时间复杂度： $O (n)$
空间复杂度： $O (n)$

反序列化

时间复杂度： $O (n)$
空间复杂度： $O (n)$

其中 $n$ 为二叉树节点的个数

最长递增子序列

🔒题目

原题链接：300.最长递增子序列

🔑题解

解法一：暴力DFS（超时 22 / 54）

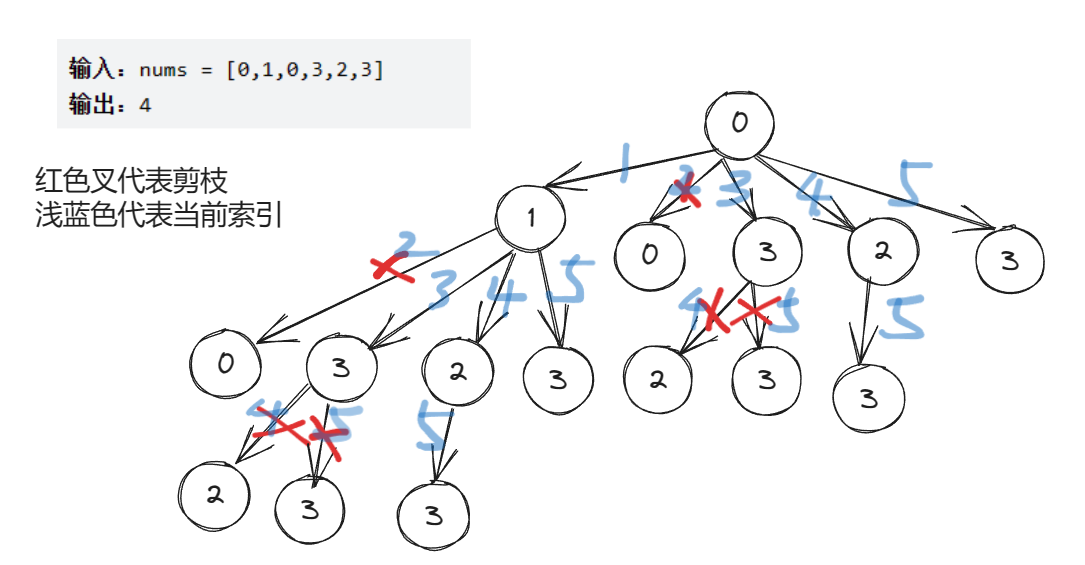
PS：画的有点丑，但是能看明白就行(●ˇ∀ˇ●)
```
/**
 * @author ghp
 * @title
 * @description
 */
public class Solution {
    public int lengthOfLIS(int[] nums) {
        // 最长递增子序列的长度
        int maxLength = 0;
        // DFS遍历每一个节点
        for (int i = 0; i < nums.length; i++) {
            int length = dfs(nums, i, Integer.MIN_VALUE);
            maxLength = Math.max(maxLength, length);
        }
        return maxLength;
    }

    private int dfs(int[] nums, int index, int preLen) {
        if (index == nums.length) {
            // 达到数组末尾，返回长度为0
            return 0;
        }
        int len1 = 0;
        if (nums[index] > preLen) {
            // 当前元素大于前一个元素，可以选择当前元素作为递增子序列的一部分
            len1 = 1 + dfs(nums, index + 1, nums[index]);
        }
        // 不选择当前元素，继续寻找下一个递增子序列
        int len2 = dfs(nums, index + 1, preLen);
        // 返回选择当前元素和不选择当前元素中的较长子序列的长度
        return Math.max(len1, len2);
    }
}
```
复杂度分析：
- 时间复杂度： $O(2^n)$ ，每一个节点都有选和不选两种情况，所以总的来说是 $2^n$
- 空间复杂度： $O (l o g n)$ ，空间复杂度为递归的最大深度，最大深度是树的最大高度
其中 $n$ 为数组中元素的个数

代码优化：时间优化

我们可以通过记忆化搜索来大幅度提高搜索的速度，我们需要新增一个memo数组，memo[i][j]表示以第i个元素为结尾、且第j个元素为上一个结尾元素的最长递增子序列的长度。

为了新增一个记忆搜索功能，我们需要对上面代码进行一个微型改造，我们在DFS搜索时，不能像前面一样传递上一个节点的长度，而是需要传递上一个节点的索引，这样我们才能够使用memo数组对当前状态进行标记，下面的示意图是添加了记忆数组之后的搜索

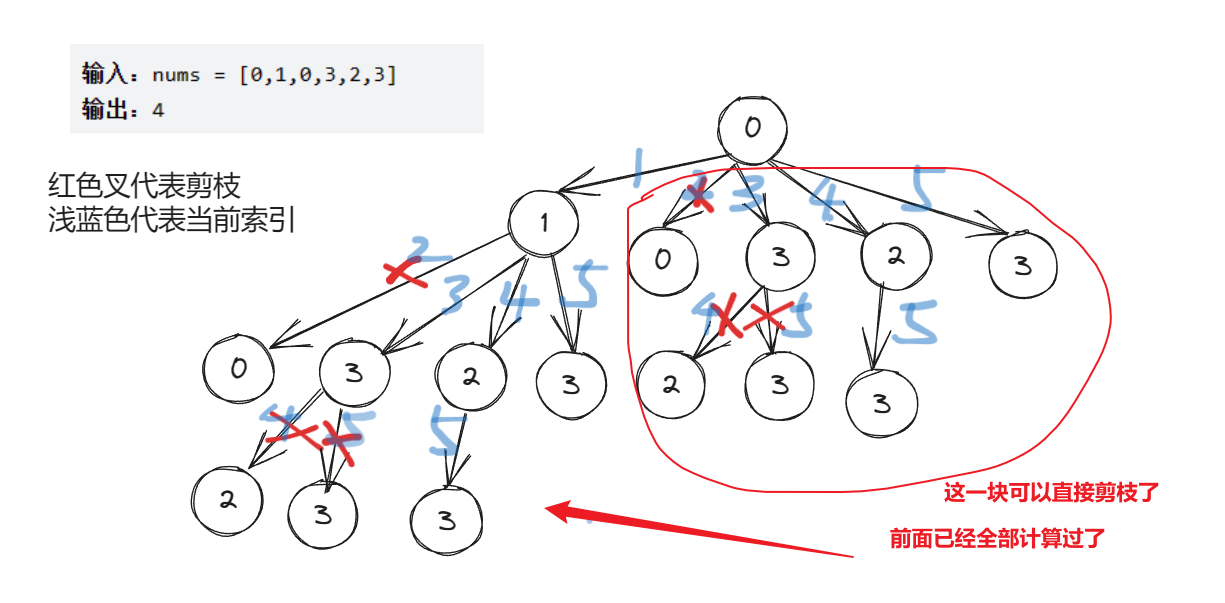
通过Debug也可以看出来，每进行一次DFS，都可以直接将当前节点到其它任意节点的距离计算出来，这样就能大幅度进行剪枝了。比如上图，0到1这条路径，就可以计算出0到其它节点（1，0，3，2，3）的距离了，后面的路径0到0、0到3、0到2、0到3就不用再去重新遍历了，而是直接拿我们缓存在memo中的路径
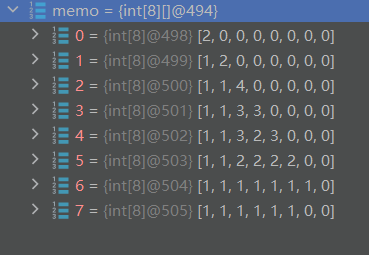
```
public class Solution {
    public int lengthOfLIS(int[] nums) {
        int maxLength = 1;
        // 记录节点的状态 memo[i][j]表示索引为j的节点到索引为i的节点的最长递增节点数
        int[][] memo = new int[nums.length][nums.length];
        // DFS搜索每一个节点
        for (int i = 0; i < nums.length; i++) {
            maxLength = Math.max(maxLength, dfs(nums, i, i, memo));
        }
        return maxLength;
    }

    private int dfs(int[] nums, int curIndex, int preIndex, int[][] memo) {
        if (curIndex >= nums.length) {
            // 后面已经没有节点了，结束搜索
            return 0;
        }
        if (memo[curIndex][preIndex] > 0) {
            // preIndex到curIndex这个状态已计算过，直接返回
            return memo[curIndex][preIndex];
        }
        int len1 = 0;
        if (preIndex == curIndex || nums[curIndex] > nums[preIndex]) {
            // 当前元素大于前一个元素，可以选择当前元素作为递增子序列的一部分
            len1 = 1 + dfs(nums, curIndex + 1, curIndex, memo);
        }
        // 不选择当前元素，继续寻找下一个递增子序列
        int len2 = dfs(nums, curIndex + 1, preIndex, memo);
        // 缓存preIndex到curIndex这个状态
        memo[curIndex][preIndex] = Math.max(len1, len2);
        // 返回选择当前元素和不选择当前元素中的较长子序列的长度
        return memo[curIndex][preIndex];
    }
}
```
记忆搜索是经典的拿时间换空间，时间复杂度虽然没有变，但是却大大缩减了搜索结果的时间，空间复杂度提高了

复杂度分析：
- 时间复杂度： $O(2^n)$ ，每一个节点都有选和不选两种情况，所以总的来说是 $2^n$
- 空间复杂度： $O(n^2)$ ，memo占用 $n^2$ 的空间
其中 $n$ 为数组中元素的个数

备注：将 memo[curIndex][preIndex] 转换为 memo[preIndex][curIndex] 是不可行的。这是因为 preIndex 的值是固定的，是遍历时的前一个索引，而 curIndex 是在不断递增变化的。

如果我们将 memo[curIndex][preIndex] 转换为 memo[preIndex][curIndex]，则无法正确存储和查找子问题的解决方案。由于 curIndex 不断增加，我们无法准确地映射到递归调用中的子问题。

代码优化：空间优化

我们可以发现memo每进行一次DFS都只用到了一列的数据，所以我们完全可以将二维的memo压缩为一维的memo
```
public class Solution {
    public int lengthOfLIS(int[] nums) {
        int maxLength = 1;
        int[] memo = new int[nums.length];
        Arrays.fill(memo, 1);
        for (int i = 0; i < nums.length; i++) {
            maxLength = Math.max(maxLength, dfs(nums, i, memo));
        }
        return maxLength;
    }

    private int dfs(int[] nums, int curIndex, int[] memo) {
        if (curIndex >= nums.length) {
            return 0;
        }
        if (memo[curIndex] > 1) {
            return memo[curIndex];
        }
        int maxLen = 1;
        for (int i = curIndex + 1; i < nums.length; i++) {
            if (nums[i] > nums[curIndex]) {
                maxLen = Math.max(maxLen, 1 + dfs(nums, i, memo));
            }
        }
        memo[curIndex] = maxLen;
        return maxLen;
    }
}
```
复杂度分析：
- 时间复杂度： $O(n^2)$ ，每一个节点都有选和不选两种情况，所以总的来说是 $2^n$
- 空间复杂度： $O (n)$ ，memo占用 $n$ 的空间
其中 $n$ 为数组中元素的个数

解法二：动态规划

我们需要构建一个dp[i]，dp[i]表示以nums[i]结尾的最长递增子序列的长度，此时我们可以知道当前第i个节点结尾的最长递增子序列，一定是由前面的节点转移而来的，至于是前面哪一个节点，我们无法直接确定，所以此时需要遍历前面 i+1个节点，在遍历的同时，我们不断更新当前的 dp[i]，遍历完毕，即可得到当前最大长度。

不知道为什么感觉动态规划比前面的DFS要简单多了

import java.util.Arrays;

/**
 * @author ghp
 * @title
 * @description
 */
public class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        int maxLength = 1;
        int[] dp = new int[nums.length];
        // 每一个节点自身的初始长度都是1
        Arrays.fill(dp, 1);
        // 遍历每一个节点
        for (int i = 1; i < nums.length; i++) {
            // 遍历0~i之间的节点，计算出所有以当前nums[i]结尾的最长递增子序列的长度
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            maxLength = Math.max(maxLength, dp[i]);
        }
        return maxLength;
    }
}

复杂度分析：

时间复杂度： $O(n^2)$
空间复杂度： $O (n)$

其中 $n$ 为数组中元素的个数

解法三：动态规划+二分查找

来自：300. 最长递增子序列（动态规划 + 二分查找，清晰图解） - 最长递增子序列 - 力扣（LeetCode）

class Solution {
    public int lengthOfLIS(int[] nums) {
        int len = 1, n = nums.length;
        if (n == 0) {
            return 0;
        }
        int[] d = new int[n + 1];
        d[len] = nums[0];
        for (int i = 1; i < n; ++i) {
            if (nums[i] > d[len]) {
                d[++len] = nums[i];
            } else {
                int l = 1, r = len, pos = 0; // 如果找不到说明所有的数都比 nums[i] 大，此时要更新 d[1]，所以这里将 pos 设为 0
                while (l <= r) {
                    int mid = (l + r) >> 1;
                    if (d[mid] < nums[i]) {
                        pos = mid;
                        l = mid + 1;
                    } else {
                        r = mid - 1;
                    }
                }
                d[pos + 1] = nums[i];
            }
        }
        return len;
    }
}

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/longest-increasing-subsequence/solution/zui-chang-shang-sheng-zi-xu-lie-by-leetcode-soluti/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析：

时间复杂度： $O (n l o g n)$
空间复杂度： $O (n)$

其中 $n$ 为数组中元素的个数

删除无效括号

先缓缓w(ﾟДﾟ)w，明天在写把，不然今天任务完不成了

🔒题目

原题链接：301.删除无效括号

🔑题解

解法一：暴力
复杂度分析：
- 时间复杂度： $O(n^2)$
- 空间复杂度： $O (1)$
其中 $n$ 为数组中元素的个数
解法二：哈希表

这个太强了，时间复杂度直接变成 $O (n)$ ，它是利用Map的Key不能重复的特性，来判断元素是否符合要求。
复杂度分析：
- 时间复杂度： $O (n)$
- 空间复杂度： $O (n)$
其中 $n$ 为数组中元素的个数

参考题解：

9种方法（可能是目前最全的），拓展大家思路 - 寻找重复数 - 力扣（LeetCode）
使用「二分查找」搜索一个有范围的整数（结合「抽屉原理」） - 寻找重复数 - 力扣（LeetCode）
【图解】dfs + bfs + 后序遍历 + 其他思路 - 二叉树的序列化与反序列化 - 力扣（LeetCode）# 【LeetCode热题100】打卡第44天：倒数第30~25题