24考研数据结构-线性表3

news2025/1/10 21:30:38

目录

      • 2.4 线性表的链式表示
      • 2.4.0 引入的原因
        • 2.4.1 单链表的定义
      • 2.4.2 单链表的两种实现形式
        • 2.4.2.1 不带头结点的单链表
        • 2.4.2.2 带头结点的单链表
        • 2.4.2.3知识回顾与重要考点
        • 2.4.3.1 带头结点的单链表按位序插入节点
        • 2.4.3.2 单链表的插入节点的时间复杂度
        • 2.4.3.3 不带头结点的单链表的插入节点
        • 2.4.3.4 不带头结点的单链表的插入节点的时间复杂度
        • 2.4.3.5 指定节点的后插操作
        • 2.4.3.6 指定节点的前插操作
        • 2.4.3.7 按位序删除节点（带头结点）
        • 2.4.3.8 按位序删除节点（带头结点）的时间复杂度
        • 2.4.3.9 指定结点的删除
        • 2.4.3.10 知识回顾与重要考点

2.4 线性表的链式表示

2.4.0 引入的原因

在这里插入图片描述

2.4.1 单链表的定义

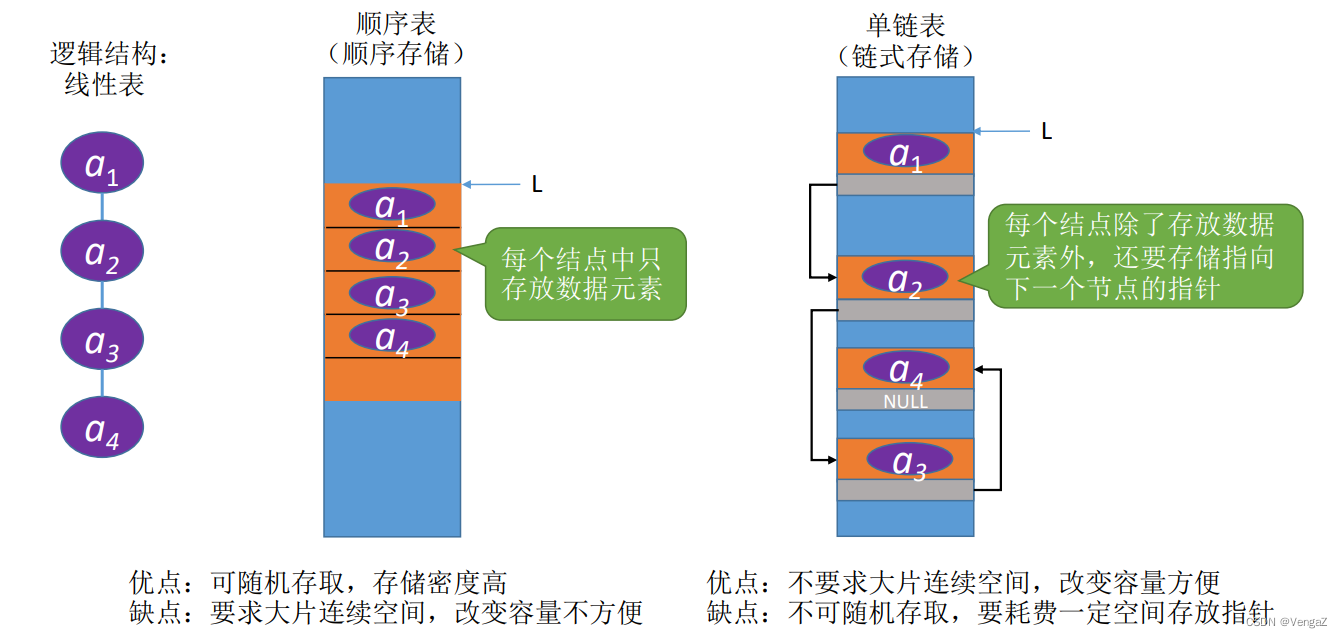
定义： 线性表的链式存储又称单链表，它是指通过一组任意的存储单元来存储线性表中的数据元素。

typedef struct LNode{//定义单链表结点类型
    ElemType data; //数据域
    struct LNode *next;//指针域
}LNode, *LinkList;

可以利用typedef关键字——数据类型重命名：type<数据类型><别名>

等价：

struct LNode{//定义单链表结点类型
    ElemType data; //数据域
    struct LNode *next;//指针域
}
typedef struct LNode LNode；
typedef struct LNode *LinkList;

在这里插入图片描述
在这里插入图片描述

2.4.2 单链表的两种实现形式

2.4.2.1 不带头结点的单链表

typedef struct LNode{  //数据结构是存有本身的数据以及下一个的地址
    ElemType data;
    struct LNode *next;
}LNode, *LinkList;

//初始化一个空的单链表
bool InitList(LinkList &L){  //注意用引用 &
    L = NULL; //空表，暂时还没有任何结点；直接指定一个空指针当作头指针，
    //这个空指针指向的下一个元素就应该是有数据的第一个节点
    return true;
}

void test(){
    LinkList L;  //声明一个指向单链表的指针: 头指针
    //初始化一个空表
    InitList(L);
    //...
}

//判断单链表是否为空
bool Empty(LinkList L){
    if (L == NULL)
        return true;
    else
        return false;
}

2.4.2.2 带头结点的单链表

头指针：开辟空间返回的指向单链表的起始物理地址的指针，仅是一个指针

不带头节点的单链表的头指针指向的头节点有数据；
带头节点的单链表的头指针指向的头节点是没有数据的

头结点：代表链表上头指针指向的第一个结点。

typedef struct LNode{
    ElemType data;
    struct LNode *next;
}LNode, *LinkList;

//初始化一个单链表（带头结点）
bool InitList(LinkList &L){  
    L = (LNode*) malloc(sizeof(LNode));  //头指针指向的结点——分配一个头结点
    //（不存储数据）返回的LNode*赋值给头指针，指向的就是第一个节点头节点，头节点为空。
    if (L == NULL)          //内存不足，分配失败
        return false;
    L -> next = NULL;       //头结点之后暂时还没有结点
    return true;
}

void test(){
    LinkList L;  //声明一个指向单链表的指针: 头指针
    //初始化一个空表
    InitList(L);
    //...
}

//判断单链表是否为空（带头结点）
bool Empty(LinkList L){
    if (L->next == NULL)
        return true;
    else
        return false;
}

2.4.2.3知识回顾与重要考点

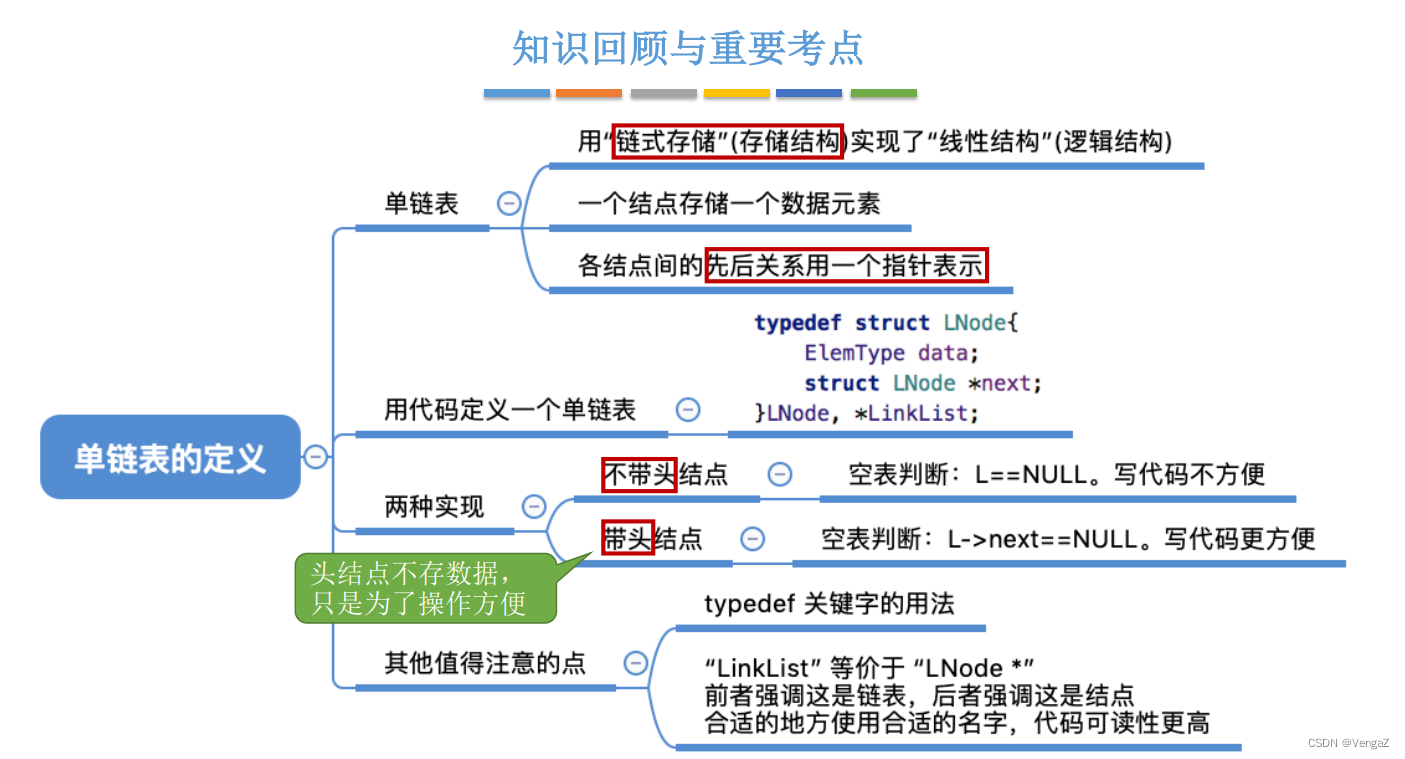
在这里插入图片描述
带头结点和不带头结点的比较：
不带头结点：写代码麻烦！对第一个数据节点和后续数据节点的处理需要用不同的代码逻辑，对空表和非空表的处理也需要用不同的代码逻辑; 头指针指向的结点用于存放实际数据;
带头结点：头指针指向的头结点不存放实际数据,头结点指向的下一个结点才存放实际数据;

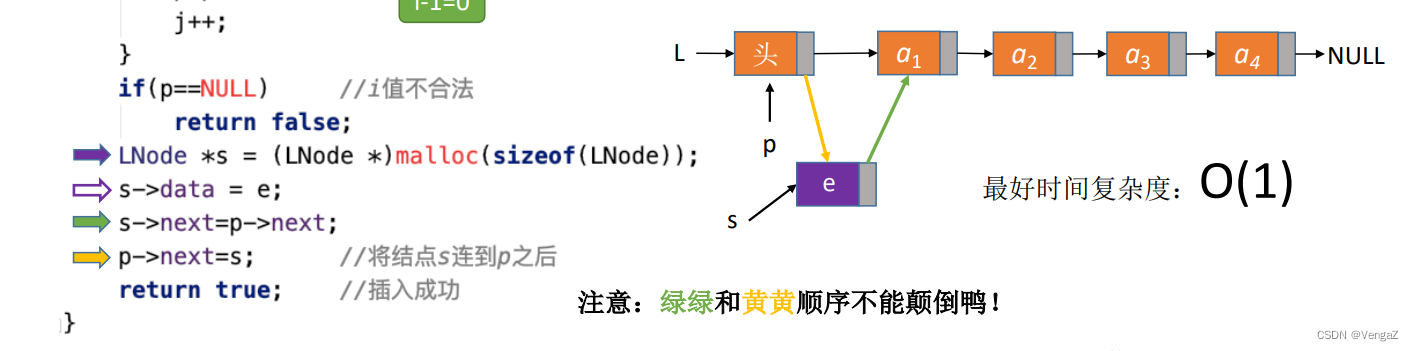
2.4.3.1 带头结点的单链表按位序插入节点

ListInsert(&L, i, e) ;在表L中的第i个位置上插入指定元素e = 找到第i-1个结点(前驱结点)，将新结点插入其后；其中头结点可以看作第0个结点，故i=1时也适用。

typedef struct LNode{
    ElemType data;
    struct LNode *next;
}LNode, *LinkList;

//在第i个位置插入元素e（带头结点）
bool ListInsert(LinkList &L, int i, ElemType e){  
    //判断i的合法性, i是位序号(从1开始)
    if(i<1)
        return False;
    
    LNode *p;       //指针p指向当前扫描到的结点 
    int j=0;        //当前p指向的是第几个结点，=0则表示目前指向头节点，链表下标从1开始
    p = L;          //L指向头结点，头结点是第0个结点（不存数据）

    //循环找到第i-1个结点，因为要修改插入节点位子的前一个节点的指针
    while(p!=NULL && j<i-1){     //如果i>lengh, p最后会等于NULL
        p = p->next;             //p指向下一个结点
        j++;
    }

    if (p==NULL)                 //i值不合法
        return false;
    
    //在第i-1个结点后插入新结点
    LNode *s = (LNode *)malloc(sizeof(LNode)); //申请一个结点空间用于存放新的节点的数据
    s->data = e;  //让新的节点的数据为e
    s->next = p->next;  //让新的节点的
    p->next = s;                 //将结点s连到p后,后两步千万不能颠倒qwq

    return true;
}
注意:
1.j = 0,是头节点的位置，这个0是方便编程的，链表的下标是从1开始
2.需要找到的位置是i-1，因为需要修改插入节点位置的上一个LNode的指针，让它指向插入节点
3.倘若最后查找出来的p指针指向null，则说明i的值不合法，因为第i-1个元素已经是null了，超过了最后一个节点，指向了null
4.最重要的LNode的指针逻辑：首先申请一个新的LNode地址指针，指向新分配的空间；设置这个LNode的数据值为e；新分配的LNode的下一个位置指向p的下一个位置（绿色线）；再将当前的p指针的下一位指向新分配的LNode（黄色线）。
5.倘若绿色黄色颠倒，则会产生LNode指向自己而不是原本的p指向的后边的链表，后边的链表就会丢失。

在这里插入图片描述

2.4.3.2 单链表的插入节点的时间复杂度

最好情况：插入表头 O（1）
最坏情况：插入表尾O（n）
平均时间复杂度：O（n）
插入每个位置（n+1个位置）的概率都是 1 n + 1 \frac{1}{n+1} n+11​， ( 1 + n ) n 2 ∗ 1 n + 1 = n 2 \frac{(1+n)n}{2}*\frac{1}{n+1} =\frac{n}{2} 2(1+n)n​∗n+11​=2n​

2.4.3.3 不带头结点的单链表的插入节点

ListInsert(&L, i, e) :在表L中的第i个位置上插入指定元素e = 找到第i-1个结点(前驱结点)，将新结点插入其后; 因为不带头结点，所以不存在“第0个”结点，因此！i=1 时，需要特殊处理——插入(删除)第1个元素时，需要更改头指针L;

typedef struct LNode{
    ElemType data;
    struct LNode *next;
}LNode, *LinkList;

bool ListInsert(LinkList &L, int i, ElemType e){
    if(i<1)
        return false;
    
    //插入到第1个位置时的操作有所不同！
    if(i==1){
        LNode *s = (LNode *)malloc(size of(LNode));
        s->data =e;
        s->next =L;
        L=s;          //头指针指向新结点
        return true;
    }

    //i>1的情况与带头结点一样！唯一区别是j的初始值为1
    LNode *p;       
    int j=1;        
    p = L;          //L指向第一个结点（存数据）

    //循环找到第i-1个结点
    while(p!=NULL && j<i-1){     //如果i>lengh, p最后会等于NULL
        p = p->next;             //p指向下一个结点
        j++;
    }

    if (p==NULL)                 //i值不合法
        return false;
    
    //在第i-1个结点后插入新结点
    LNode *s = (LNode *)malloc(sizeof(LNode)); //申请一个结点
    s->data = e;
    s->next = p->next;
    p->next = s;          
    return true;

}
注意:
1.最重要的LNode的i = 1的指针逻辑：首先申请一个新的LNode地址指针，指向新分配的空间；设置这个LNode的数据值为e；新分配的LNode的下一个位置指向头指针L指向的位置（s->next =L; 绿色线）；再将当前的头指针L指向新分配的LNode（L=s; 黄色线）。
2.不带头节点插入删除i=1的节点，需要修改头指针，所以不带头指针需要考虑对i=1操作的情况会比较麻烦。
3.此时对于定位的j，需要设置初始值为1，而不是带头节点的0。
4.若i不为1，则操作都一样

2.4.3.4 不带头结点的单链表的插入节点的时间复杂度

同上

最好情况：插入表头 O（1）
最坏情况：插入表尾O（n）
平均时间复杂度：O（n）
插入每个位置（n+1个位置）的概率都是 1 n + 1 \frac{1}{n+1} n+11​， ( 1 + n ) n 2 ∗ 1 n + 1 = n 2 \frac{(1+n)n}{2}*\frac{1}{n+1} =\frac{n}{2} 2(1+n)n​∗n+11​=2n​

2.4.3.5 指定节点的后插操作

InsertNextNode(LNode *p, ElemType e): 给定一个结点p，在其之后插入元素e; 根据单链表的链接指针只能往后查找，故给定一个结点p，那么p之后的结点我们都可知，但是p结点之前的结点无法得知;

typedef struct LNode{
    ElemType data;
    struct LNode *next;
}LNode, *LinkList;

bool InsertNextNode(LNode *p, ElemType e){
    if(p==NULL){
        return false;
    }

    LNode *s = (LNode *)malloc(sizeof(LNode));
    //某些情况下分配失败，比如内存不足
    if(s==NULL)
        return false;
    s->data = e;          //用结点s保存数据元素e 
    s->next = p->next;
    p->next = s;          //将结点s连到p之后

    return true;
}                         //平均时间复杂度 = O(1)


//有了后插操作，那么在第i个位置上插入指定元素e的代码可以改成：
bool ListInsert(LinkList &L, int i, ElemType e){  
    if(i<1)
        return False;
    
    LNode *p;       //指针p指向当前扫描到的结点 
    int j=0;        //当前p指向的是第几个结点
    p = L;          //L指向头结点，头结点是第0个结点（不存数据）

    //循环找到第i-1个结点
    while(p!=NULL && j<i-1){     //如果i>lengh, p最后4鸟会等于NULL
        p = p->next;             //p指向下一个结点
        j++;
    }

    return InsertNextNode(p, e)
}
注意:
1.bool InsertNextNode(LNode *p, ElemType e)，后插操作判断给的指针是否是空指针；判断是否内存分配失败
2.找到第i-1个节点就可以调用这个后插函数 return InsertNextNode(p, e)
3.时间复杂度为O（1） 
    if(p==NULL){
        return false;
    }

    LNode *s = (LNode *)malloc(sizeof(LNode));
    //某些情况下分配失败，比如内存不足
    if(s==NULL)
        return false;

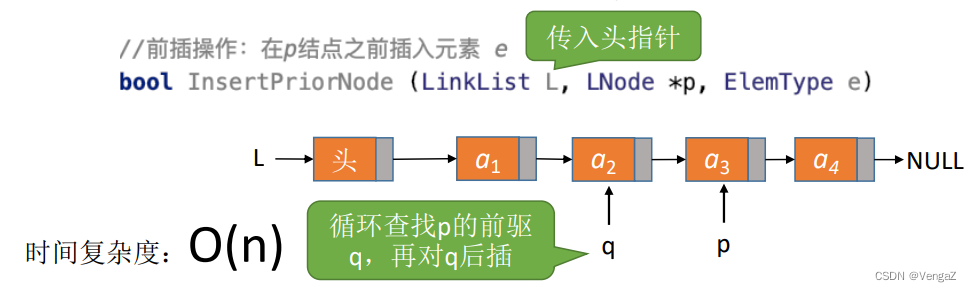
2.4.3.6 指定节点的前插操作

InsertPriorNode(LNode *p, ElenType e) 思想：设待插入结点是s，将s插入到p的前面。我们仍然可以将s插入到*p的后面。然后将p->data与s->data交换，这样既能满足了逻辑关系，又能是的时间复杂度为O(1).

  1. 传入头指针，从头开始遍历寻找到指定节点前驱
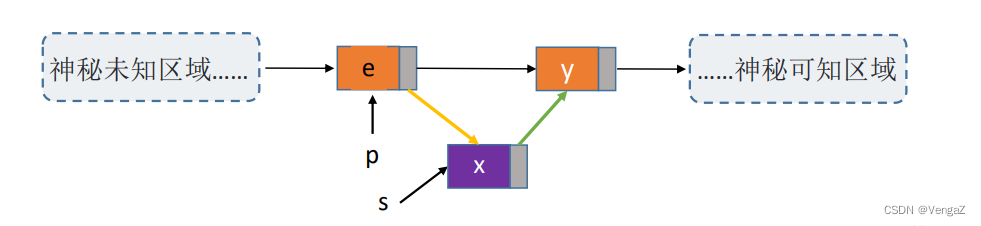
    在这里插入图片描述

  2. 不传入头节点，使用交换指定节点和需要插入节点的数据，完成操作
    该方法时间复杂度为O（1)

在这里插入图片描述

//前插操作：在p结点之前插入元素e
bool InsertPriorNode(LNode *p, ElenType e){
    if(p==NULL)
        return false;
    
    LNode *s = (LNode *)malloc(sizeof(LNode));
    if(s==NULL) //内存分配失败
        return false;

    //重点来了！
    s->next = p->next;
    p->next = s;       //新结点s连到p之后
    s->data = p->data; //将p中元素复制到s
    p->data = e;       //p中元素覆盖为e

    return true；
}  //时间复杂度为O(1)
  1. 王道书上版本（传入指定节点与需要插入的节点）
bool InsertPriorNode(LNode *p, LNode *s){
    if(p==NULL || S==NULL)
        return false;
    
    s->next = p->next;
    p->next = s;  ///s连接到p
    ELemType temp = p->data;  //声明临时变量temp存储p的数据
    p->data = s->data;  //用需要插入节点的数据覆盖p中的数据
    s->data = temp;  //将临时变量赋值给s的数据部分

    return true;
}
 



ELemType temp = p->data;  //交换数据域部分，声明临时变量temp存储p的数据

2.4.3.7 按位序删除节点（带头结点）

ListDelete(&L, i, &e) : 删除操作，删除表L中第i个位置的元素，并用e返回删除元素的值;头结点视为“第0个”结点；

思路：找到第i-1个结点，将其指针指向第i+1个结点，并释放第i个结点；

typedef struct LNode{
    ElemType data;
    struct LNode *next;
}LNode, *LinkList;

bool ListDelete(LinkList &L, int i, ElenType &e){
    if(i<1) return false;

    LNode *p;       //指针p指向当前扫描到的结点 
    int j=0;        //当前p指向的是第几个结点
    p = L;          //L指向头结点，头结点是第0个结点（不存数据）

    //循环找到第i-1个结点
    while(p!=NULL && j<i-1){     //如果i>lengh, p最后会等于NULL
        p = p->next;             //p指向下一个结点
        j++;
    }

    if(p==NULL) 
        return false;
    if(p->next == NULL) //第i-1个结点之后已无其他结点
        return false;

    LNode *q = p->next;         //令q指向被删除的结点
    e = q->data;                //用e返回被删除元素的值
    p->next = q->next;          //将*q结点从链中“断开”
    free(q)                     //释放结点的存储空间

    return true;
}

2.4.3.8 按位序删除节点（带头结点）的时间复杂度

同上

最好情况：插入表头 O（1）
最坏情况：插入表尾O（n）
平均时间复杂度：O（n）

2.4.3.9 指定结点的删除

bool DeleteNode(LNode *p){
    if(p==NULL)
        return false;
    
    LNode *q = p->next;      //令q指向*p的后继结点
    p->data = p->next->data; //让p和后继结点交换数据域
    p->next = q->next;       //将*q结点从链中“断开”
    free(q);
    return true;
} //时间复杂度 = O(1)

倘若需要删除的是最后一个节点，则时间复杂度为O（n），因为找不到下一个节点不能跟它交换数据，再free它。只能从链表的头开始寻找到该指针的前继节点，将它指向null。

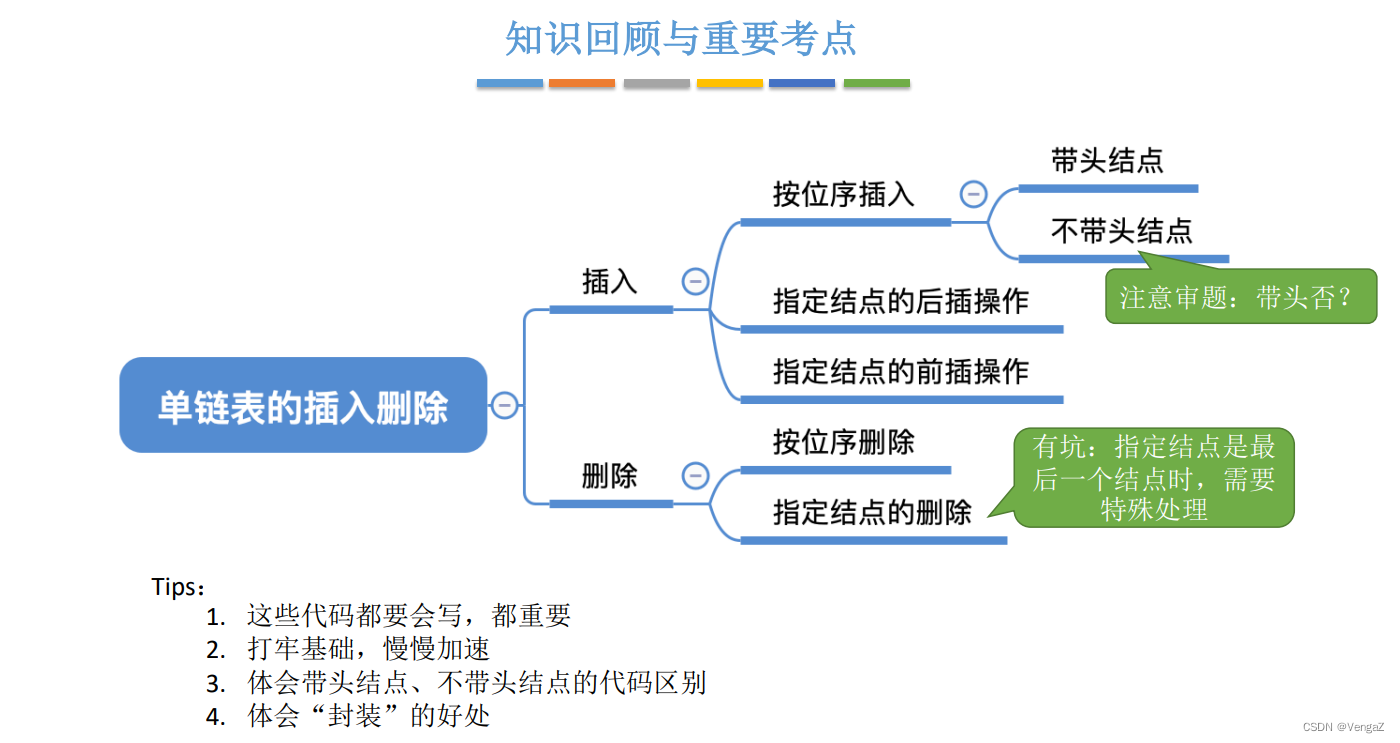
2.4.3.10 知识回顾与重要考点

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/787384.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Ceph网络模型

Ceph网络模型

Ceph网络模型 Ceph 生产环境中一般分为两个网段公有网络: 用于用户的数据通信集群网络: 用于集群内部的管理通信
阅读更多...
mac m1 触控栏TouchBar功能栏异常

mac m1 触控栏TouchBar功能栏异常

电脑可能在高温下运行时间过长&#xff0c;导致TouchBar之前正常显示的调整屏幕亮度与调整声音等功能的按钮均丢失&#xff0c;然后看了一眼键盘设置&#xff0c;设置也是正常的&#xff0c;已勾选显示功能栏 下面请看 如何在MacBook Pro&#xff08;macOS Monterey&#xff0…
阅读更多...
2023年深圳杯数学建模赛题浅析

2023年深圳杯数学建模赛题浅析

由于今明两日由于一些不可避免的事情&#xff0c;这里仅仅先给大家简单写一个赛题浅析&#xff0c;详细过程步骤思路以及讲解视频预计后天发布 A题 影响城市居民身体健康的因素分析 A题以慢性病为命题背景&#xff0c;给出数据以及题目初步来看来看为一个数据处理数据分析的综…
阅读更多...
elasticsearch查询操作（DSL语句方式）

elasticsearch查询操作（DSL语句方式）

说明&#xff1a;本文介绍在kibana&#xff0c;es的可视化界面上对文档的查询操作&#xff1b; 添加数据 先使用API&#xff0c;创建索引库&#xff0c;并且把数据从MySQL中查出来&#xff0c;传到ES上&#xff0c;参考&#xff08;http://t.csdn.cn/NaTHg&#xff09; 索引库…
阅读更多...
Ceph部署方法介绍

Ceph部署方法介绍

Ceph部署方法介绍 Installing Ceph — Ceph Documentation Ceph环境规划 admin是一个部署节点
阅读更多...
Centos7 扩容（LVM 和非 LVM）

Centos7 扩容（LVM 和非 LVM）

一、磁盘扩容方式 CentOS 系统的磁盘扩容可以分为两种方式&#xff1a;LVM 管理和非 LVM 管理。 LVM 管理的分区和传统分区方式是可以共存的。在同一个系统中&#xff0c;你可以同时使用 LVM 管理的分区和传统分区。 例如&#xff0c;在 CentOS 系统中&#xff0c;你可以选择将…
阅读更多...
《重构的时机和方法》书籍推荐

《重构的时机和方法》书籍推荐

《重构的时机和方法》是一本由克里斯蒂安克劳森(Christian Clausen)所著&#xff08;郭涛翻译&#xff09;的软件工程经典之作。本书全面介绍了重构的概念、原则和方法&#xff0c;为软件开发者提供了一系列宝贵的指导和实践经验。在这篇书评文章中&#xff0c;我将从内容、实用…
阅读更多...
Linux环境安装Tomcat

Linux环境安装Tomcat

在tomcat官网(下载路径)下载好tomcat压缩包 上传服务器压缩到/usr/tomcat目录下 tar -zxvf xxx.tar.gz 配置tomcat环境变量 export CATALINA_HOME/usr/tomcat/apache-tomcat-8.5.56 export CATALINE_BASE/usr/tomcat/apache-tomcat-8.5.56 export PATH$PATH:$CATALINA_BASE/bi…
阅读更多...
阿克曼转向模型介绍

阿克曼转向模型介绍

阿克曼转向模型介绍 目录 阿克曼转向模型介绍是什么&#xff1f;基本原理应用与改进 是什么&#xff1f; 阿克曼转向是一种现代汽车的转向方式&#xff0c;在汽车转弯的时候&#xff0c;内外轮转过的角度不一样&#xff0c;内侧轮胎转弯半径小于外侧轮胎。 它描述了汽车转向系…
阅读更多...
Spring中如何用注解方式存取JavaBean？有几种注入方式？

Spring中如何用注解方式存取JavaBean？有几种注入方式？

博主简介&#xff1a;想进大厂的打工人博主主页&#xff1a;xyk:所属专栏: JavaEE进阶 本篇文章将讲解如何在spring中使用注解的方式来存取Bean对象&#xff0c;spring提供了多种注入对象的方式&#xff0c;常见的注入方式包括 构造函数注入&#xff0c;Setter 方法注入和属性…
阅读更多...
TypeError: can‘t convert np.ndarray of type numpy.object_.

TypeError: can‘t convert np.ndarray of type numpy.object_.

在处理数据集的时候出现报错&#xff1a; TypeError: can’t convert np.ndarray of type numpy.object_. The only supported types are: float64, float32, float16, complex64, complex128, int64, int32, int16, int8, uint8, and bool. train_labels torch.tensor(train…
阅读更多...
手机怎么压缩pdf？这种压缩方法简单易用

手机怎么压缩pdf？这种压缩方法简单易用

手机怎么压缩pdf&#xff1f;PDF文件是我们生活和工作中常用的一种文档格式&#xff0c;但是有时候PDF文件的大小会很大&#xff0c;不方便发送和存储。那么&#xff0c;如何在手机上压缩PDF文件呢&#xff1f;下面就给大家介绍一种简单好用的压缩方法。 今天要给大家介绍的这款…
阅读更多...
甘特图的发展史

甘特图的发展史

目录 背景: 过程: 总结&#xff1a; 背景: 1910年代初为了管理工程项目的进度而创造了甘特图。 1917年&#xff0c;美国工程师亨利甘特(Henry Laurence Gantt)首次提出了甘特图的概念。他是一位工程师和管理学家&#xff0c;设计了一种图表&#xff0c;用于显示进度成产仅度…
阅读更多...
毕业生求职招聘网站的设计与实现JAVA（SpringBoot+VUE+Mysql）

毕业生求职招聘网站的设计与实现JAVA（SpringBoot+VUE+Mysql）

由SpringBootVUEMysql实现的网站的设计 功能模块 设计思路&#xff1a;主要分为管理员、毕业生、招聘企业三大身份模块 首先是登录界面 注册界面 其次就是公共页面 公共页面又分为首页、空中宣讲会、招聘岗位、求职信息、论坛信息、试卷列表、招聘资讯、个人中心和后台管理、…
阅读更多...
【原创】内网穿透案例

【原创】内网穿透案例

案列一&#xff08;Frp内网渗透&#xff09; 大概图列网上随便找的&#xff0c;路线是这个样子 这里选用ctfshow的一道命令执行题 由Frp实现内网访问及扫描 1.传入一句话&#xff0c;上线蚁剑http://b85fdf24-b98e-4810-9e76-a038a8987630.challenge.ctf.show:8080/?cecho…
阅读更多...
C语言--位段

C语言--位段

C语言—位段 文章目录 C语言---位段一、位段是什么&#xff1f;二、位段的内存分配三&#xff0c;位段的跨平台问题四&#xff0c;位段的应用 一、位段是什么&#xff1f; 位段的声明和结构是类似的&#xff0c;有两个不同&#xff1a; 位段的成员必须是 int、unsigned int 或…
阅读更多...
代码随想录day12 | [前、中、后、层]二叉树的遍历迭代法和递归法

代码随想录day12 | [前、中、后、层]二叉树的遍历迭代法和递归法

文章目录 一、前后中序递归法二、前后序迭代法三、中序遍历迭代法四、层序遍历 递归三部曲&#xff1a; 1️⃣ 第一步确定递归函数的返回值和参数 2️⃣第二步确定递归的终止条件 3️⃣第三步确定单层递归处理的逻辑 一、前后中序递归法 前序遍历二叉树 class Solution { pr…
阅读更多...
vue三级路由的写法

vue三级路由的写法

{path: "/trafficmanagement",component: Layout,redirect: "/trafficmanagement",alwaysShow: true,meta: {title: "通行模块",icon: "excel",},children: [{path: "carline",name: "carline",alwaysShow: true,…
阅读更多...
数据结构day8（2023.7.25）

数据结构day8（2023.7.25）

一、排序算法 排序&#xff1a;把无需序列转换为有序序列的一种算法。 内排&#xff1a;在计算机内存中实现的排序算法【多用适用于数据量较小的情况】 外排&#xff1a;在计算机内存以及外部介质实现的排序算法【先内存&#xff0c;在外部】 排序的分类&#xff1a; 交换排…
阅读更多...
Godot 4 源码分析 - 获取脚本

Godot 4 源码分析 - 获取脚本

获取属性列表 今天搂草打兔&#xff0c;取得了脚本内容 因为已能取得属性值&#xff0c;那就再进一步&#xff0c;取得属性名列表 if (SameText(drGet.propertyName, "propertyNames", DRGRAPH_FLAG_CASESENSITIVE)) {List<PropertyInfo> *p_list new List…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023