说明：

1. Kernel版本：4.14
2. ARM64处理器，Contex-A53，双核
3. 使用工具：Source Insight 3.5， Visio

1. 介绍

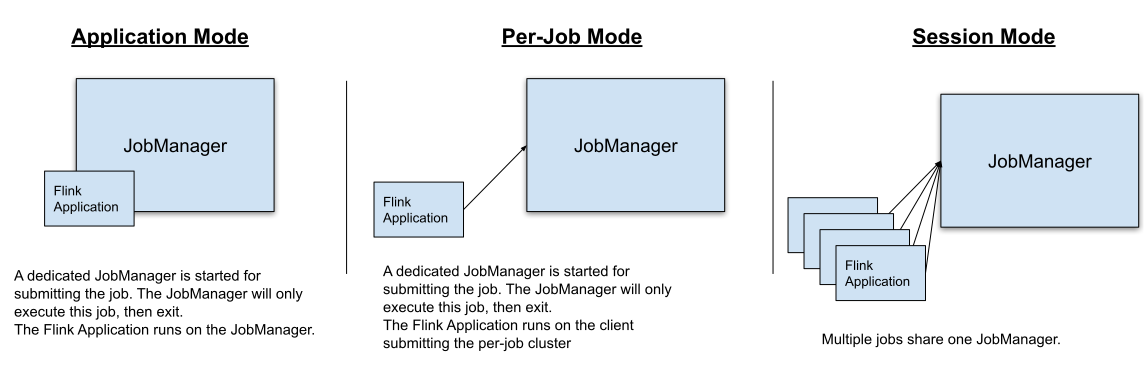
SMP, Symmetric Multi-Processor，相对于单核处理器来说，SMP实现了真正严格意义上的并发。通常SMP的启动，会先让Boot Core启动，Secondary Cores会等待Boot Core来唤醒。

顺带参考下Arm Cortex-A53 MPCore Processor, Revision:r0p4文档中的图片，描述一下SMP中CPU Core的配置接口及功能模块：

• 配置接口

• 功能框图

  资料直通车：Linux内核源码技术学习路线+视频教程内核源码

学习直通车：Linux内核源码内存调优文件系统进程管理设备驱动/网络协议栈

2. 流程

当然，这篇文章的核心，当然是下边这张图片了：

图中从Uboot到内核分析了流程：

SMP启动的时候，Secondary CPU是可能处在WFI或者WFE状态，以前的内核中会进入WFI状态，然后可以通过arch_send_call_function_ipi_mask接口去boot Secondary CPU。而我分析的这个版本中，处理器会在Uboot中进入WFE状态，后续在启动过程中，会有两次进入WFE状态的情况，Boot CPU需要两次通过SEV指令才能真正把CPU1启动起来。

在Kernel启动的过程中，涉及到smp操作的时，最终会调用到底层的CPU操作函数集cpu_ops，而cpu_ops是可以选择smp_spin_table的形式，或者psci的形式，如果选择psci的形式，那么就涉及到底层的Arm Trusted Firmware。整体的流程比较复杂，后续有机会接触再深入分析。