雅可比迭代法与高斯-塞德尔迭代法
雅可比迭代法
- 例一
{ 10 x 1 − x 2 − 2 x 3 = 7.2 − x 1 + 10 x 2 − 2 x 3 = 8.3 − x 1 − x 2 + 5 x 3 = 4.2 \left\{\begin{array}{l} 10 x_{1}-x_{2}-2 x_{3}=7.2 \\ -x_{1}+10 x_{2}-2 x_{3}=8.3 \\ -x_{1}-x_{2}+5 x_{3}=4.2 \end{array}\right. ⎩⎨⎧10x1−x2−2x3=7.2−x1+10x2−2x3=8.3−x1−x2+5x3=4.2
分别从上面的三个方程中分离出 x 1 、 x 2 、 x 3 x_1、x_2、x_3 x1、x2、x3
x 1 = 0.1 x 2 + 0.2 x 3 + 0.72 x 2 = 0.1 x 1 + 0.2 x 3 + 0.83 x 3 = 0.2 x 1 + 0.2 x 2 + 0.84 → { x 1 ( k + 1 ) = 0.1 x 2 ( k ) + 0.2 x 3 ( k ) + 0.72 x 2 ( k + 1 ) = 0.1 x 1 ( k ) + 0.2 x 3 ( k ) + 0.83 x 3 ( k + 1 ) = 0.2 x 1 ( k ) + 0.2 x 2 ( k ) + 0.84 \begin{aligned} x_{1} & =0.1 x_{2}+0.2 x_{3}+0.72 \\ x_{2} & =0.1 x_{1}+0.2 x_{3}+0.83 \\ x_{3} & =0.2 x_{1}+0.2 x_{2}+0.84 \end{aligned} \to \left\{\begin{array}{l} x_{1}^{(k+1)}=0.1 x_{2}^{(k)}+0.2 x_{3}^{(k)}+0.72 \\ x_{2}^{(k+1)}=0.1 x_{1}^{(k)}+0.2 x_{3}^{(k)}+0.83 \\ x_{3}^{(k+1)}=0.2 x_{1}^{(k)}+0.2 x_{2}^{(k)}+0.84 \end{array}\right. x1x2x3=0.1x2+0.2x3+0.72=0.1x1+0.2x3+0.83=0.2x1+0.2x2+0.84→⎩⎪⎨⎪⎧x1(k+1)=0.1x2(k)+0.2x3(k)+0.72x2(k+1)=0.1x1(k)+0.2x3(k)+0.83x3(k+1)=0.2x1(k)+0.2x2(k)+0.84
取x=0,迭代过程如下图:
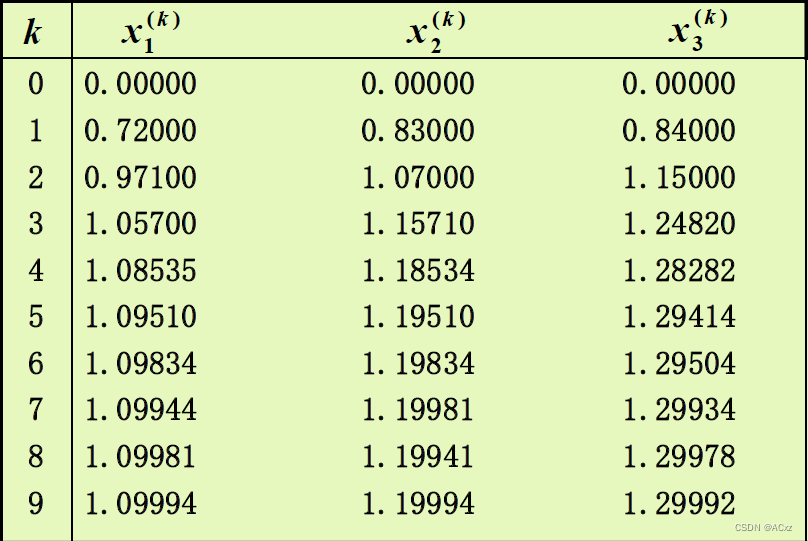
- Jacobi迭代分量形式
{ a 11 x 1 + a 12 x 2 + … + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + … + a 2 n x n = b 2 … … … … a n 1 x 1 + a n 2 x 2 + … + a n n x n = b n \left\{\begin{array}{l} a_{11} x_{1}+a_{12} x_{2}+\ldots+a_{1 n} x_{n}=b_{1} \\ a_{21} x_{1}+a_{22} x_{2}+\ldots+a_{2 n} x_{n}=b_{2} \\ \ldots \quad \ldots \quad \ldots \quad \ldots \\ a_{n 1} x_{1}+a_{n 2} x_{2}+\ldots+a_{n n} x_{n}=b_{n} \end{array}\right. ⎩⎪⎪⎨⎪⎪⎧a11x1+a12x2+…+a1nxn=b1a21x1+a22x2+…+a2nxn=b2…………an1x1+an2x2+…+annxn=bn
由 a i i ≠ 0 a_{ii} \ne 0 aii=0可得 ( i = 1 、 2 、 3 、 . . . 、 n ) (i=1、2、3、...、n) (i=1、2、3、...、n):
{ x 1 = 1 a 11 ( − a 12 x 2 − … − a 1 n x n + b 1 ) x 2 = 1 a 22 ( − a 21 x 1 − … − a 2 n x n + b 2 ) ⋯ ⋯ ⋯ x n = 1 a n n ( − a n 1 x 1 − … − a n n − 1 x n − 1 + b n ) ⇔ x i ( k + 1 ) = 1 a i i ( b i − ∑ j = 1 、 j ≠ i n a i j x j ( k ) ) \left\{\begin{array}{l} x_{1}=\frac{1}{a_{11}}\left(-a_{12} x_{2}-\ldots-a_{1 n} x_{n}+b_{1}\right) \\ x_{2}=\frac{1}{a_{22}}\left(-a_{21} x_{1}-\ldots-a_{2 n} x_{n}+b_{2}\right) \\ \cdots \quad \cdots \quad \cdots \\ x_{n}=\frac{1}{a_{n n}}\left(-a_{n 1} x_{1}-\ldots-a_{n n-1} x_{n-1}+b_{n}\right) \end{array}\right. \Leftrightarrow x_{i}^{(k+1)}=\frac{1}{a_{i i}}\left(b_{i}-\sum_{{j=1 \\ 、 j \neq i}}^{n} a_{i j} x_{j}^{(k)}\right) ⎩⎪⎪⎨⎪⎪⎧x1=a111(−a12x2−…−a1nxn+b1)x2=a221(−a21x1−…−a2nxn+b2)⋯⋯⋯xn=ann1(−an1x1−…−ann−1xn−1+bn)⇔xi(k+1)=aii1⎝⎛bi−j=1、j=i∑naijxj(k)⎠⎞
高斯-赛德尔迭代法
Jacobi迭代法并不利用这些最新的近似值计算,所以对迭代方法进行更新。
- 对例一修正:
{ x 1 ( k + 1 ) = 0.1 x 2 ( k ) + 0.2 x 3 ( k ) + 0.72 x 2 ( k + 1 ) = 0.1 x 1 ( k + 1 ) + 0.2 x 3 ( k ) + 0.83 x 3 ( k + 1 ) = 0.2 x 1 ( k + 1 ) + 0.2 x 2 ( k + 1 ) + 0.84 \left\{\begin{array}{l} \boldsymbol{x}_{1}^{(k+1)}=0.1 \boldsymbol{x}_{2}^{(k)}+0.2 \boldsymbol{x}_{3}^{(k)}+0.72 \\ \boldsymbol{x}_{2}^{(k+1)}=0.1 \boldsymbol{x}_{1}^{(k+1)}+0.2 \boldsymbol{x}_{3}^{(k)}+0.83 \\ \boldsymbol{x}_{3}^{(k+1)}=0.2 \boldsymbol{x}_{1}^{(k+1)}+0.2 \boldsymbol{x}_{2}^{(k+1)}+0.84 \end{array}\right. ⎩⎪⎨⎪⎧x1(k+1)=0.1x2(k)+0.2x3(k)+0.72x2(k+1)=0.1x1(k+1)+0.2x3(k)+0.83x3(k+1)=0.2x1(k+1)+0.2x2(k+1)+0.84
迭代过程如下:
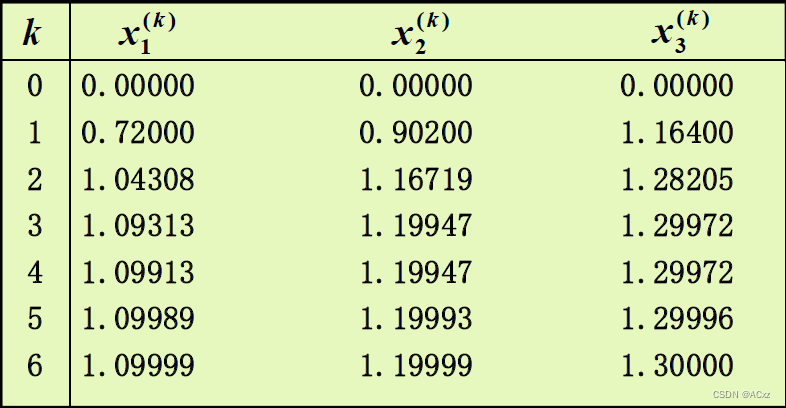
- 迭代分量形式
x 1 ( k + 1 ) = 1 a 11 ( − a 12 x 2 ( k ) − a 13 x 3 ( k ) − a 14 x 4 ( k ) − ⋯ − a 1 n x n ( k ) + b 1 ) x 2 ( k + 1 ) = 1 a 22 ( − a 21 x 1 ( k + 1 ) − a 23 x 3 ( k ) − a 24 x 4 ( k ) − ⋯ − a 2 n x n ( k ) + b 2 ) x 3 ( k + 1 ) = 1 a 33 ( − a 31 x 1 ( k + 1 ) − a 32 x 2 ( k + 1 ) − a 34 x 4 ( k ) − ⋯ − a 3 n x n ( k ) + b 3 ) ⋮ x n ( k + 1 ) = 1 a n n ( − a n 1 x 1 ( k + 1 ) − a n 2 x 2 ( k + 1 ) − a n 3 x 3 ( k + 1 ) − ⋯ − a n n − 1 x n − 1 ( k + 1 ) + b n ) ⇔ x i ( k + 1 ) = 1 a i i ( b i − ∑ j = 1 i − 1 a i j x j ( k + 1 ) − ∑ j = i + 1 n a i j x j ( k ) ) \begin{array}{l} x_{1}^{(k+1)}=\frac{1}{a_{11}}\left(-a_{12} x_{2}^{(k)}-a_{13} x_{3}^{(k)}-a_{14} x_{4}^{(k)}-\cdots-a_{1 n} x_{n}^{(k)}+b_{1}\right) \\ x_{2}^{(k+1)}=\frac{1}{a_{22}}\left(-a_{21} x_{1}^{(k+1)}-a_{23} x_{3}^{(k)}-a_{24} x_{4}^{(k)}-\cdots-a_{2 n} x_{n}^{(k)}+b_{2}\right) \\ x_{3}^{(k+1)}=\frac{1}{a_{33}}\left(-a_{31} x_{1}^{(k+1)}-a_{32} x_{2}^{(k+1)}-a_{34} x_{4}^{(k)}-\cdots-a_{3 n} x_{n}^{(k)}+b_{3}\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ x_{n}^{(k+1)}=\frac{1}{a_{n n}}\left(-a_{n 1} x_{1}^{(k+1)}-a_{n 2} x_{2}^{(k+1)}-a_{n 3} x_{3}^{(k+1)}-\cdots-a_{n n-1} x_{n-1}^{(k+1)}+b_{n}\right) \\ \end{array}\\\Leftrightarrow x_{i}^{(k+1)}=\frac{1}{a_{i i}}\left(b_{i}-\sum_{j=1}^{i-1} a_{i j} x_{j}^{(k+1)}-\sum_{j=i+1}^{n} a_{i j} x_{j}^{(k)}\right) x1(k+1)=a111(−a12x2(k)−a13x3(k)−a14x4(k)−⋯−a1nxn(k)+b1)x2(k+1)=a221(−a21x1(k+1)−a23x3(k)−a24x4(k)−⋯−a2nxn(k)+b2)x3(k+1)=a331(−a31x1(k+1)−a32x2(k+1)−a34x4(k)−⋯−a3nxn(k)+b3) ⋮xn(k+1)=ann1(−an1x1(k+1)−an2x2(k+1)−an3x3(k+1)−⋯−ann−1xn−1(k+1)+bn)⇔xi(k+1)=aii1(bi−j=1∑i−1aijxj(k+1)−j=i+1∑naijxj(k)) - 矩阵形式
x ⃗ ( k + 1 ) = − D − 1 ( L x ⃗ ( k + 1 ) + U x ˉ ( k ) ) + D − 1 b ⃗ ⇔ ( D + L ) x ⃗ ( k + 1 ) = − U x ⃗ ( k ) + b ⃗ ⇔ x ⃗ ( k + 1 ) = − ( D + L ) − 1 U ⏟ B x ˉ ( k ) + ( D + L ) − 1 ⏟ f ˉ b ⃗ \begin{array}{l} \vec{x}^{(k+1)}=-D^{-1}\left(L \vec{x}^{(k+1)}+U \bar{x}^{(k)}\right)+D^{-1} \vec{b} \\ \Leftrightarrow(D+L) \vec{x}^{(k+1)}=-U \vec{x}^{(k)}+\vec{b} \\ \Leftrightarrow \vec{x}^{(k+1)}=\underbrace{-(D+L)^{-1} U}_{B} \bar{x}^{(k)}+\underbrace{(D+L)^{-1}}_{\bar{f}} \vec{b} \end{array} x(k+1)=−D−1(Lx(k+1)+Uxˉ(k))+D−1b⇔(D+L)x(k+1)=−Ux(k)+b⇔x(k+1)=B −(D+L)−1Uxˉ(k)+fˉ (D+L)−1b
收敛性
- 例二
有方程组 X = B X + f X = BX + f X=BX+f
B = ( 0.9 0 0.3 0.8 ) , f = ( 1 2 ) B=\left(\begin{array}{cc} 0.9 & 0 \\ 0.3 & 0.8 \end{array}\right), f=\left(\begin{array}{l} 1 \\ 2 \end{array}\right) B=(0.90.300.8),f=(12)
判断该方程组用迭代法求解的收敛性。
解:
∥ B ∥ 1 = 1.2 , ∥ B ∥ 2 = 1.021 , ∥ B ∥ ∞ = 1.1 \|B\|_{1}=1.2,\|B\|_{2}=1.021,\|B\|_{\infty}=1.1\\ ∥B∥1=1.2,∥B∥2=1.021,∥B∥∞=1.1
但迭代矩阵谱半径 ρ ( B ) = 0.9 \rho(B)=0.9 ρ(B)=0.9,所以收敛。 - 例三
考察用Jacobi方法解方程组
{ 8 x 1 − 3 x 2 + 2 x 3 = 20 4 x 1 + 11 x 2 − x 3 = 33 6 x 1 + 3 x 2 + 12 x 3 = 36 \left\{\begin{array}{l} 8 x_{1}-3 x_{2}+2 x_{3}=20 \\ 4 x_{1}+11 x_{2}-x_{3}=33 \\ 6 x_{1}+3 x_{2}+12 x_{3}=36 \end{array}\right. ⎩⎨⎧8x1−3x2+2x3=204x1+11x2−x3=336x1+3x2+12x3=36
的收敛性。
解:
Jacobi迭代矩阵为:
B J = − [ 0 − 3 8 2 8 4 11 0 − 1 11 6 12 3 12 0 ] B_{J}=-\left[\begin{array}{ccc} 0 & -\frac{3}{8} & \frac{2}{8} \\ \frac{4}{11} & 0 & -\frac{1}{11} \\ \frac{6}{12} & \frac{3}{12} & 0 \end{array}\right] BJ=−⎣⎡0114126−83012382−1110⎦⎤
因 ∥ B J ∥ ∞ = max { 5 8 , 5 11 , 9 12 } < 1 \left\|B_{J}\right\|_{\infty}=\max \left\{\frac{5}{8}, \frac{5}{11}, \frac{9}{12}\right\}<1 ∥BJ∥∞=max{85,115,129}<1,故其Jacobi 迭代收敛。
定理一:设 x ⃗ = B x ⃗ + f ⃗ \vec{x}=B \vec{x}+\vec{f} x=Bx+f存在唯一解,则从任意 x ⃗ ( 0 ) \vec{x}^{(0)} x(0)出发,迭代 x ⃗ ( k + 1 ) = B x ⃗ ( k ) + f ⃗ \vec{x}^{(k+1)}=B \vec{x}^{(k)}+\vec{f} x(k+1)=Bx(k)+f收敛 ⇔ B k → 0 \Leftrightarrow \quad B^{k} \rightarrow 0 ⇔Bk→0。
定理二: B k → 0 ⇔ ρ ( B ) < 1 B^{k} \rightarrow 0 \Leftrightarrow \rho(B)<1 Bk→0⇔ρ(B)<1。
定理三:设有方程组 x ⃗ = B x ⃗ + f ⃗ \vec{x}=B \vec{x}+\vec{f} x=Bx+f,对任意 x ⃗ ( 0 ) \vec{x}^{(0)} x(0)和 f f f,迭代收敛充要条件为 ρ ( B ) < 1 \rho(B)<1 ρ(B)<1, ρ ( B ) \rho(B) ρ(B)越小收敛越快。
定理四: R ( B ) = − ln ρ ( B ) R(B)=-\ln\rho(B) R(B)=−lnρ(B)为迭代法的渐近收敛速度。
定理五:若A 为严格对角占优阵,则解 A x ⃗ = b A\vec{x}=b Ax=b的迭代都收敛。
超松弛迭代法
Gauss - Seidel 方法:
x
i
(
k
+
1
)
=
1
a
i
i
[
b
i
−
∑
j
=
1
i
−
1
a
i
j
x
j
(
k
+
1
)
−
∑
j
=
i
+
1
n
a
i
j
x
j
(
k
)
]
=
x
i
(
k
)
+
r
i
(
k
+
1
)
a
i
i
r
i
(
k
+
1
)
=
b
i
−
∑
j
=
1
i
−
1
a
i
j
x
j
(
k
+
1
)
−
∑
j
=
i
+
1
n
a
i
j
x
j
(
k
)
x_{i}^{(k+1)}=\frac{1}{a_{i i}}\left[b_{i}-\sum_{j=1}^{i-1} a_{i j} x_{j}^{(k+1)}-\sum_{j=i+1}^{n} a_{i j} x_{j}^{(k)}\right] =x_{i}^{(k)}+\frac{r_{i}^{(k+1)}}{a_{i i}}\\ r_{i}^{(k+1)} = b_{i}-\sum_{j=1}^{i-1} a_{i j} x_{j}^{(k+1)}-\sum_{j=i+1}^{n} a_{i j} x_{j}^{(k)}
xi(k+1)=aii1[bi−j=1∑i−1aijxj(k+1)−j=i+1∑naijxj(k)]=xi(k)+aiiri(k+1)ri(k+1)=bi−j=1∑i−1aijxj(k+1)−j=i+1∑naijxj(k)
令
x
i
(
k
+
1
)
=
x
i
(
k
)
+
ω
r
i
(
k
+
1
)
a
i
i
x_{i}^{(k+1)}=x_{i}^{(k)}+\omega \frac{r_{i}^{(k+1)}}{a_{i i}}
xi(k+1)=xi(k)+ωaiiri(k+1),希望通过选取合适
ω
\omega
ω加速收敛。该方法称松弛法。
- 矩阵形式
x i ( k + 1 ) = x i ( k ) + ω r i ( k + 1 ) a i i = ( 1 − ω ) x i ( k ) + ω a i i [ − ∑ j < i a i j x j ( k + 1 ) − ∑ j > i a i j x j ( k ) + b i ] ⇒ x ⃗ ( k + 1 ) = ( 1 − ω ) x ⃗ ( k ) + ω D − 1 [ − L x ⃗ ( k + 1 ) − U x ⃗ ( k ) + b ⃗ ] ⇒ x ⃗ ( k + 1 ) = ( D + ω L ) − 1 [ ( 1 − ω ) D − ω U ] ⏟ H ω x ⃗ ( k ) + ( D + ω L ) − 1 ω b ⃗ ⏟ f ⃗ \begin{array}{c} x_{i}^{(k+1)}=x_{i}^{(k)}+\omega \frac{r_{i}^{(k+1)}}{a_{i i}}=(1-\omega) x_{i}^{(k)}+\frac{\omega}{a_{i i}}\left[-\sum_{j<i} a_{i j} x_{j}^{(k+1)}-\sum_{j>i} a_{i j} x_{j}^{(k)}+b_{i}\right] \\ \Rightarrow \vec{x}^{(k+1)}=(1-\omega) \vec{x}^{(k)}+\omega D^{-1}\left[-L \vec{x}^{(k+1)}-U \vec{x}^{(k)}+\vec{b}\right] \\ \Rightarrow \vec{x}^{(k+1)}=\underbrace{(D+\omega L)^{-1}[(1-\omega) D-\omega U] }_{H_\omega }\vec{x}^{(k)}+\underbrace{(D+\omega L)^{-1} \omega \vec{b}}_{\vec f} \end{array} xi(k+1)=xi(k)+ωaiiri(k+1)=(1−ω)xi(k)+aiiω[−∑j<iaijxj(k+1)−∑j>iaijxj(k)+bi]⇒x(k+1)=(1−ω)x(k)+ωD−1[−Lx(k+1)−Ux(k)+b]⇒x(k+1)=Hω (D+ωL)−1[(1−ω)D−ωU]x(k)+f (D+ωL)−1ωb - 例四
A = [ 4 3 0 3 4 − 1 0 − 1 4 ] A=\left[\begin{array}{ccc} 4 & 3 & 0 \\ 3 & 4 & -1 \\ 0 & -1 & 4 \end{array}\right] A=⎣⎡43034−10−14⎦⎤
解:
A 是正定对称的三对角矩阵,
B J = D − 1 ( L + U ) = [ 0 − 0.75 0 − 0.75 0 0.25 0 0.25 0 ] det ( λ I − B J ) = λ ( λ 2 − 0.625 ) → ρ ( B J ) = 0.625 ≈ 0.790 \begin{array}{l} B_{J}=D^{-1}(L+U)=\left[\begin{array}{ccc} 0 & -0.75 & 0 \\ -0.75 & 0 & 0.25 \\ 0 & 0.25 & 0 \end{array}\right] \\ \operatorname{det}\left(\lambda I-B_{J}\right)=\lambda \left(\lambda^{2}-0.625\right) \to \rho\left(B_{J}\right)=\sqrt{0.625} \approx 0.790 \\ \end{array} BJ=D−1(L+U)=⎣⎡0−0.750−0.7500.2500.250⎦⎤det(λI−BJ)=λ(λ2−0.625)→ρ(BJ)=0.625≈0.790
据定理,有 ρ ( B G − S ) = 0.625 \rho\left(B_{G-S}\right)=0.625 ρ(BG−S)=0.625,SOR的最佳松弛因子为:
ω o p t = 2 1 + 1 − 0.625 ≈ 1.24 , ρ ( H ω ) = 0.24 \omega_{o p t}=\frac{2}{1+\sqrt{1-0.625}} \approx 1.24,\\ \rho\left(H_{\omega}\right)=0.24 ωopt=1+1−0.6252≈1.24,ρ(Hω)=0.24
可见采用最优松弛因子的SOR方法收敛速度比Jacobi方法和G-S方法快得多。