---

一、深度学习的概念

让机器自动寻找一个函数

如下图所示：

• 语音识别：输入一段语音，通过函数，得到对应的文字内容
• 图像识别：输入一张图片，通过函数，得到对应的图像类别
• 机器下围棋：输入当前“局面”，通过函数，得到下一步应该落子的坐标

---

二、函数的类型

• 回归：函数输出是一个实数。（当然还有多标签回归，输出是一个实数型的向量/矩阵）
• 分类：函数输出是一个类别。（类别通常用独热编码表示）
• 结构：函数输出是一个结构体

---

三、深度学习的步骤

3.1 定义一个参数未知的函数表达式

这一步骤在 Deep Learning 中通常表现为建立Model。比如，建立了一个3层的全连接网络，每一层是由线性层+ReLu激活函数构成的，这就是我们定义的函数表达式。在每一个线性层中，都有未知的参数 w 和 b

3.2 定义一个损失函数

损失函数的值代表了真实值与预测值之间的差距，通常来说，损失函数值越小，代表模型的预测就越接近真实值。常用的损失函数如下图所示：MAE、MSE 等

3.3 采用梯度下降法求解使得函数表达式的Loss最小的参数

---

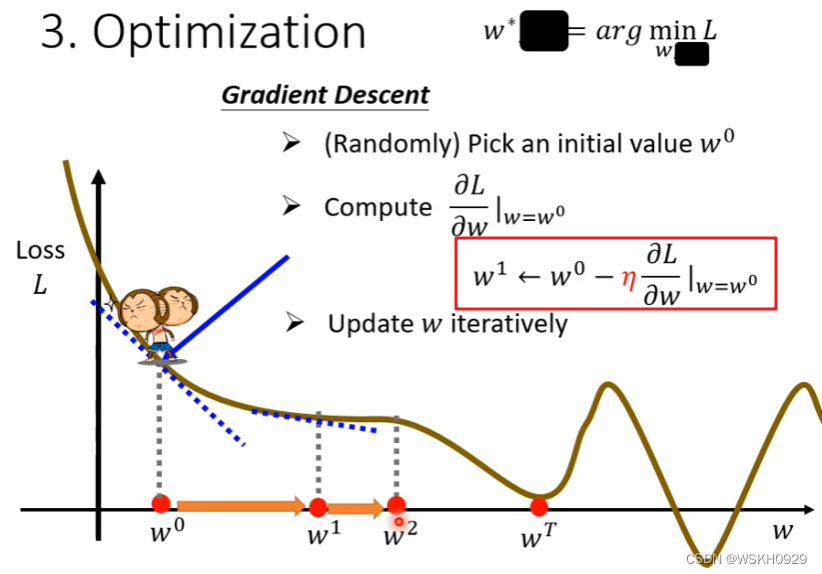
四、视频播放量预测案例

接下来，我们通过一个视频播放量的预测案例，来更深入的理解深度学习的相关概念

4.1 案例介绍和思路分析

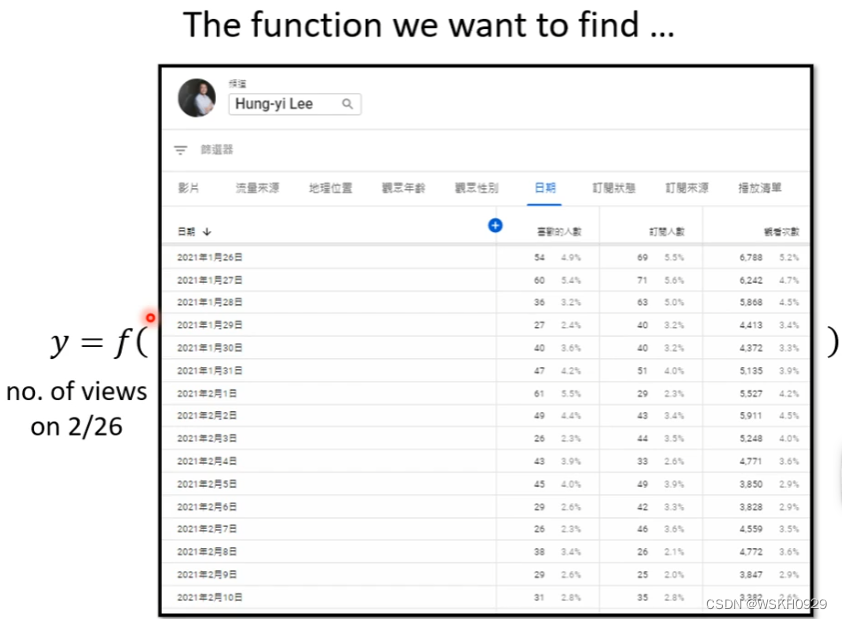
案例介绍

已知2017年-2020年的播放量数据，通过已知的数据，训练一个模型（拟合一个函数），预测未来的播放量

思路分析

按照上面介绍的三个步骤：

1. 建立参数未知的函数表达式
2. 定义损失函数
3. 梯度下降优化

实际上，很多时候步骤2和3都是比较固定的，例如回归问题，损失函数常用MSE，分类问题损失函数常用交叉熵损失等，梯度下降优化就不用说了，也是一个通用的方法。

所以，预测的效果，很大程度上取决于模型的建立，即函数表达式的选取。下面，我们会介绍几种函数表达式，带大家感受不同函数表达式的预测效果的差别，并且让大家浅浅感受一下 Why Deep Learning

4.2 线性函数表达式1

最简单的，我们可以定义一个线性的函数表达式 y = wx + b，w 是斜率，b是偏置

采用该函数表达式，相当于只根据今天的播放量对明天的播放量进行预测

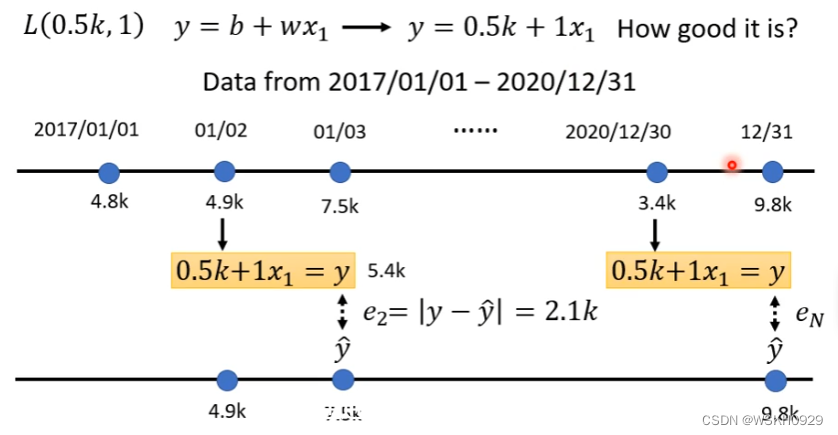
采用MAE作为损失函数，下面是损失值计算的例子

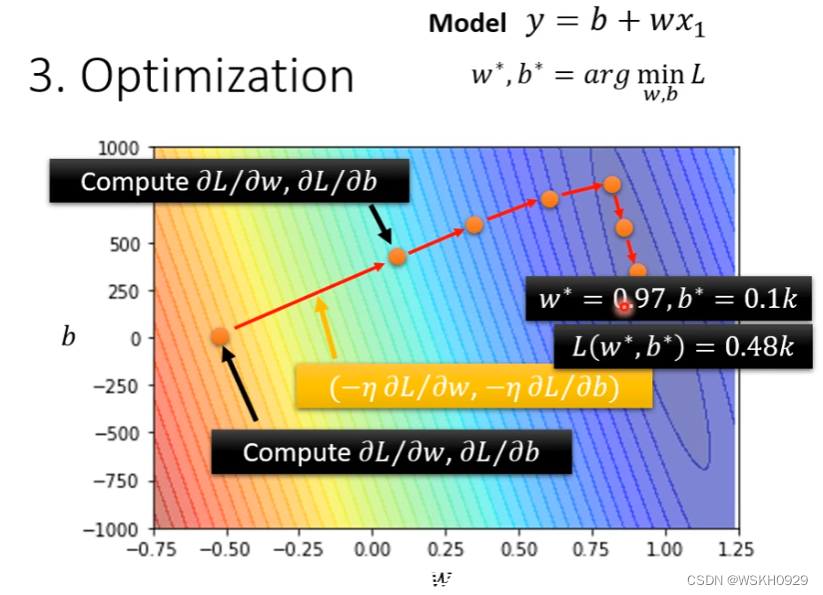
进行梯度下降优化，找到最佳参数

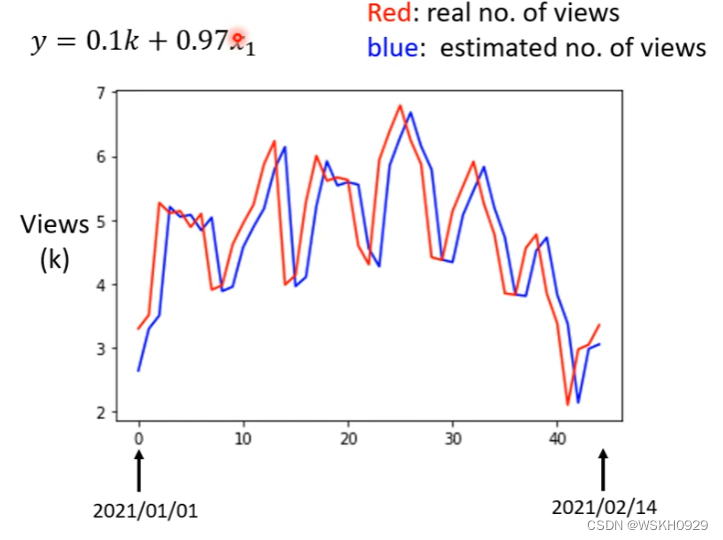
查看预测效果（红色线是真实值，蓝色线是预测值）

可以看到，预测值基本上就是真实值延后一天。这是因为我们采用的简单的线性表达式导致的，只考虑今天的播放量来预测明天

4.3 改进1：使用前一段时间的播放量来预测明天的播放量

如下图所示，将函数表达式修改一下

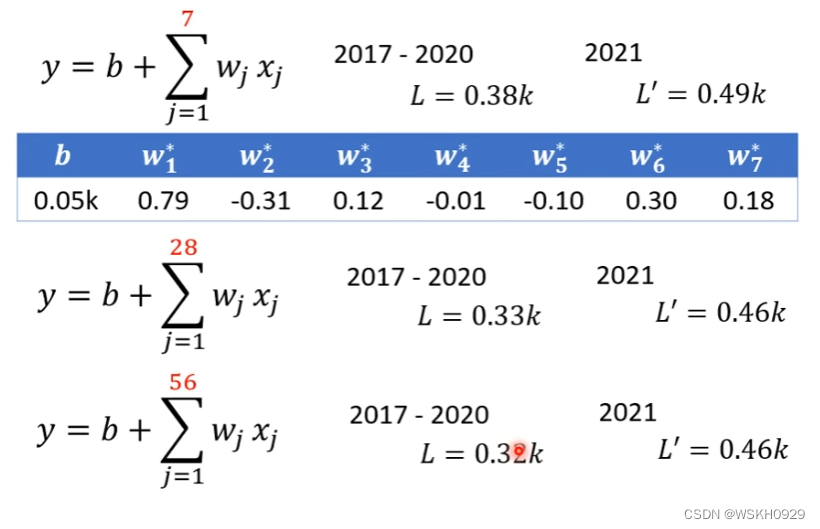
第一个函数表达式：表示用前7天的播放量预测明天的播放量
第二个函数表达式：表示用前28天的播放量预测明天的播放量
第三个函数表达式：表示用前56天的播放量预测明天的播放量

L表示模型在训练集上的损失值，L‘表示模型在测试集，也就是预测未来播放量时候的损失值

可以看出，随着采用前一段时间的天数越来越大，模型在训练集和测试集上的损失值都在减小，但是采用前一段时间的天数为56和28时的损失值相差不大，说明通过增加采用前一段时间的天数来提高莫模型精度的方法达到了瓶颈

4.4 改进2：采用非线性函数表达式

现实的曲线（红色线），可能在某一段为线性关系，但总体来看为非线性
红色的线可以看为一个常数加上很多蓝色线

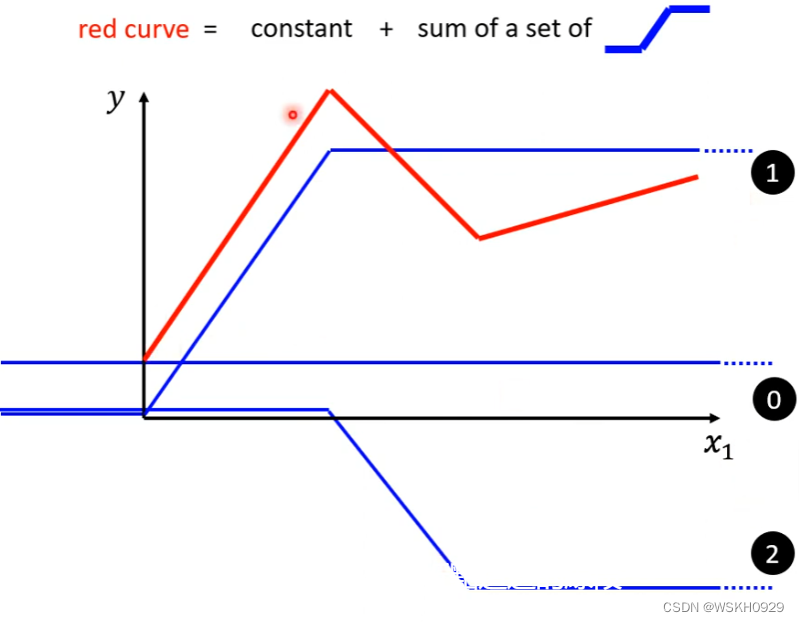
蓝色的函数：hard sigmoid
w:斜率
b：左右移动
c:高度

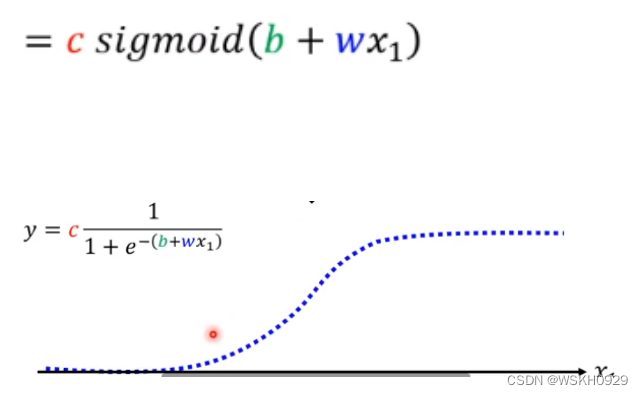
所以红色的线等于下式

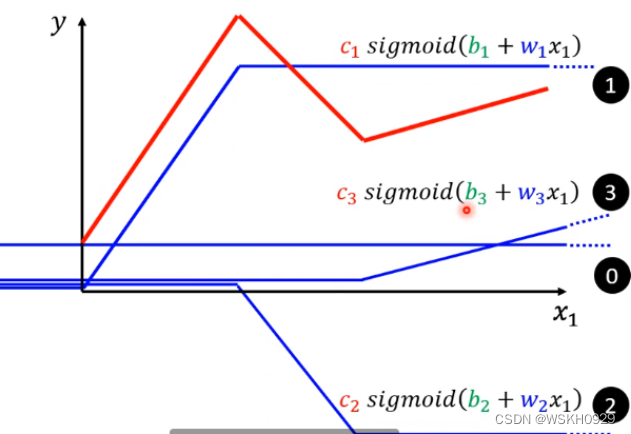
函数表达式变为下图所示

写成矩阵

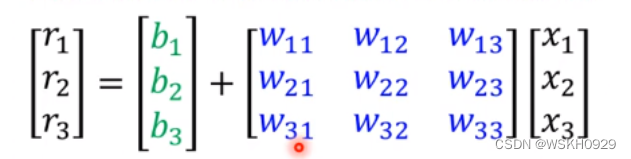
写成神经网络的样子

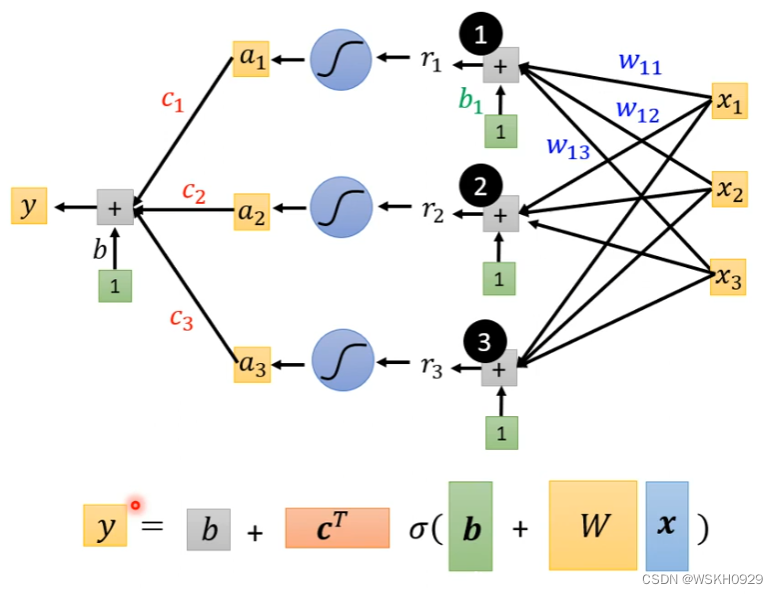
将w每一个行，b，c，常数写为一个长向量

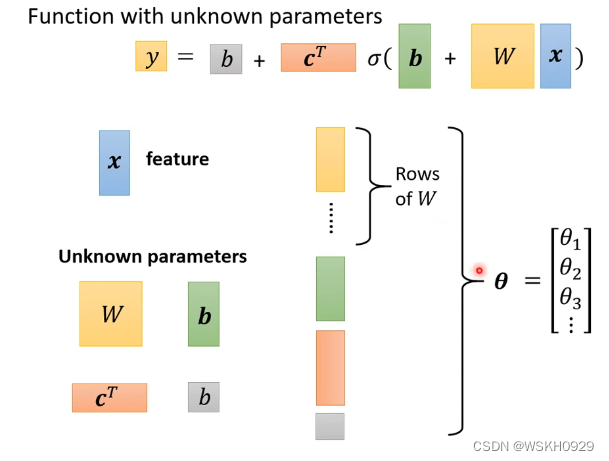
计算loss（同上面)
optimization:梯度下降法（同上面）
可以将长向量分为很多短向量，依次用梯度下降法

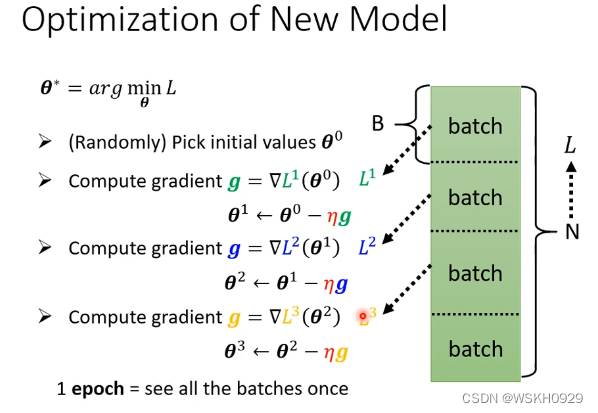
每更新一个参数叫1update ，所有的batch算完叫1epoch。

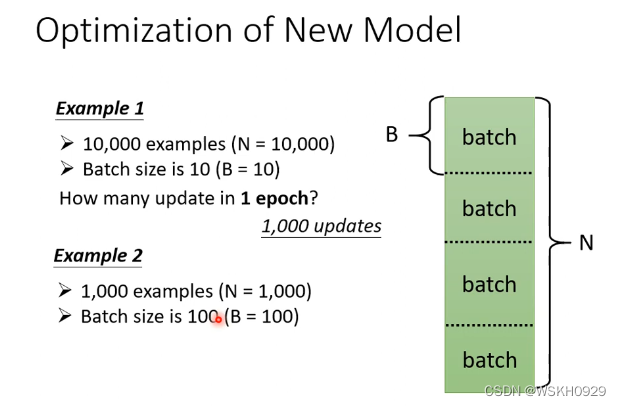
4.5 多层神经网络

上面讲的是单层神经网络。而深度学习中的“深度”指的是多层的神经网络。了解了单层神经网络的基本原理之后，要想实现多层神经网络就很简单了，只需要将第i层的输出作为第i+1层的输入即可实现

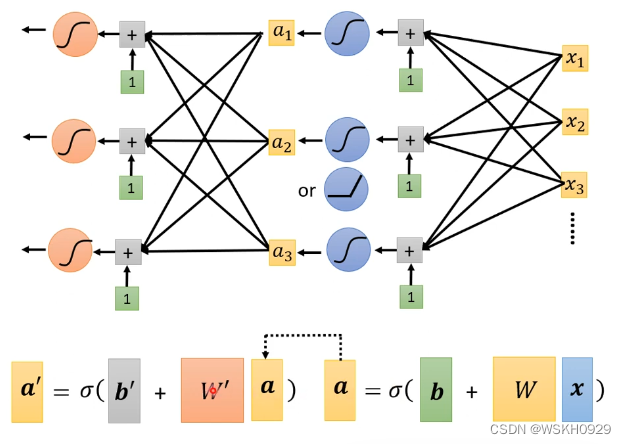
我们来看看在这个案例中，使用多层的神经网络有什么效果把

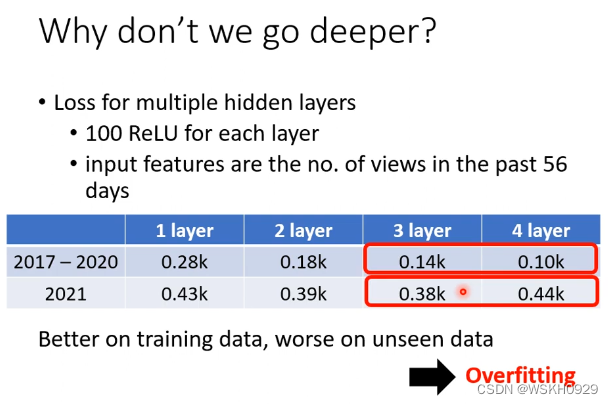
从上图我们可以看到，网络层数在1-3之间时，随着层数增加，测试集损失值在逐渐下降。但是，到第4层的时候，测试集的损失值反而上升了。我们把这种现象称为“过拟合”。

过拟合：模型过于复杂，学到了很多噪声，导致训练集loss下降，但是验证集loss上升