最全LaTeX 数学公式、字母符号、上下标、列表矩阵、公式注释、分数二进制数、分割字符、逻辑集合论、否定符号等

1. 公式示例

1. $$E(T)=\sum _{(p,q)ϵ\kappa }\mid \mid p-T_q\mid {\mid }^2$$

2. $$E(T)=\sum _{(p,q)ϵ\kappa }((p-T_q)\cdot n_p{)}^2$$

3. $$\mathbf{x}+y^{2x}\text{\hspace{1em}(hi)}$$

4. 不换行，只是显示为公式：$n_p$

5. 字体颜色：$$F=ma$$
   背景色：$$\boxed{F=ma}$$
   不加粗：$$\sum _{1\le i\le j\le n}{x}_{ij}$$
   加粗：$$\sum _{1\le \mathbf{i}\le \mathbf{j}\le \mathbf{n}}{\mathbf{x}}_{\mathbf{i}\mathbf{j}}$$

6. 下标：$$x_n$$

7. 上标：$$e^x$$

8. $$\genfrac{}{}{0ex}{}{a}{b}$$

9. $$a\text{b}c$$

10. $$\sum _{1\le i\le j\le n}{x}_{ij}$$

11. $$\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$$

12. $$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$$

13. $$\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$$

14. $$\Vert \begin{array}{cc}a& b\\ c& d\end{array}\Vert$$

15. $$\left\{\begin{array}{cc}a& b\\ c& d\end{array}\right\}$$

16. $$\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}$$

17. $$x=\{\begin{array}{ll}a& \text{if }b\\ c& \text{if }d\end{array}$$

18. $$\sum _{i=1}^n$$

19. $${\sum }_{i=1}^n$$

20. $$\underset{x}{\lim }$$

21. $${\lim }_x$$

22. $$\text{x^2}$$

2.1 字母符号组合

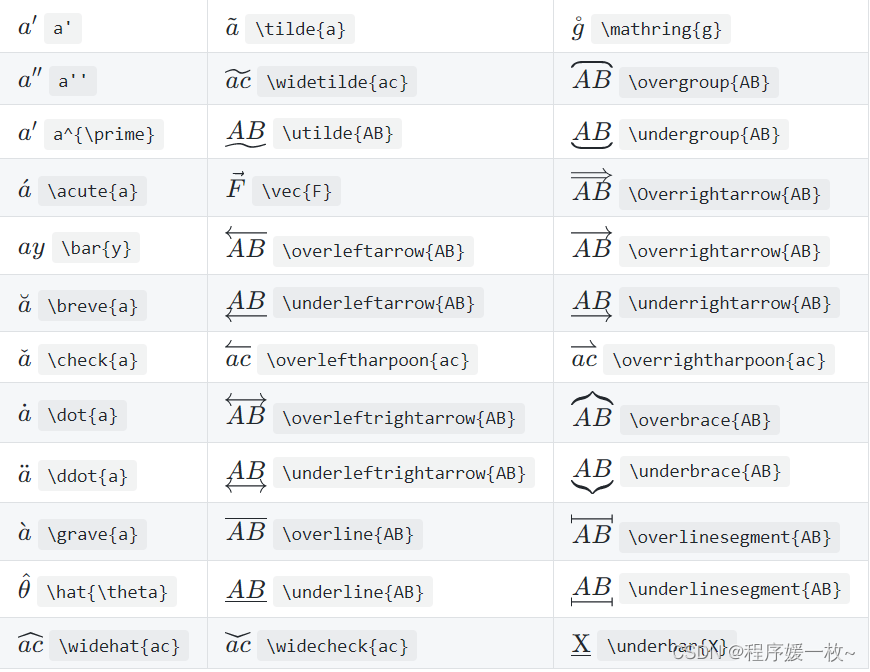
2.2 列表矩阵

2.3 公式注释

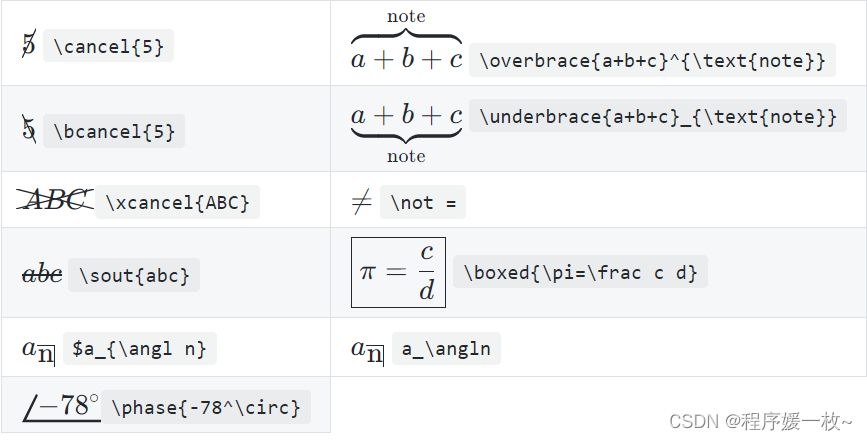
2.4 垂直布局

2.5 分割字符

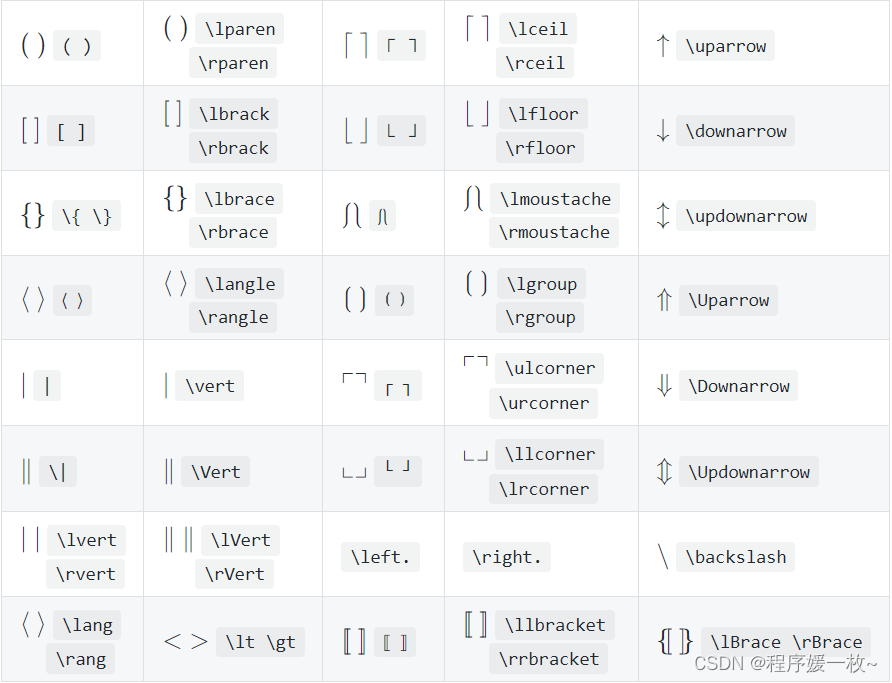
2.5 希腊字母和Unicode字符

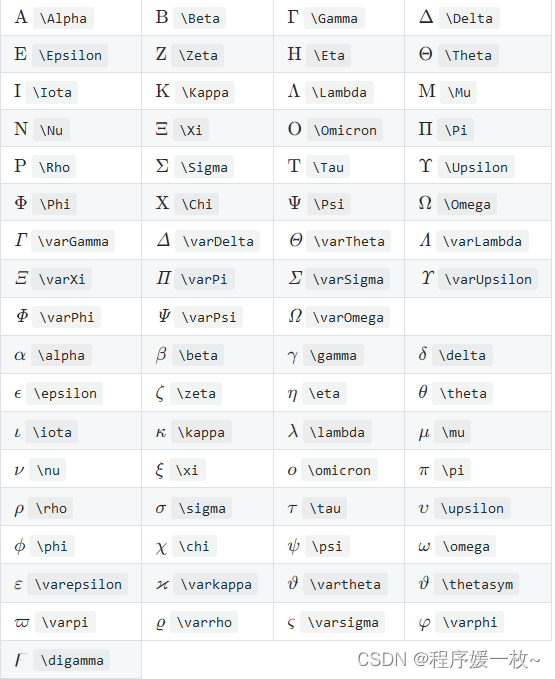
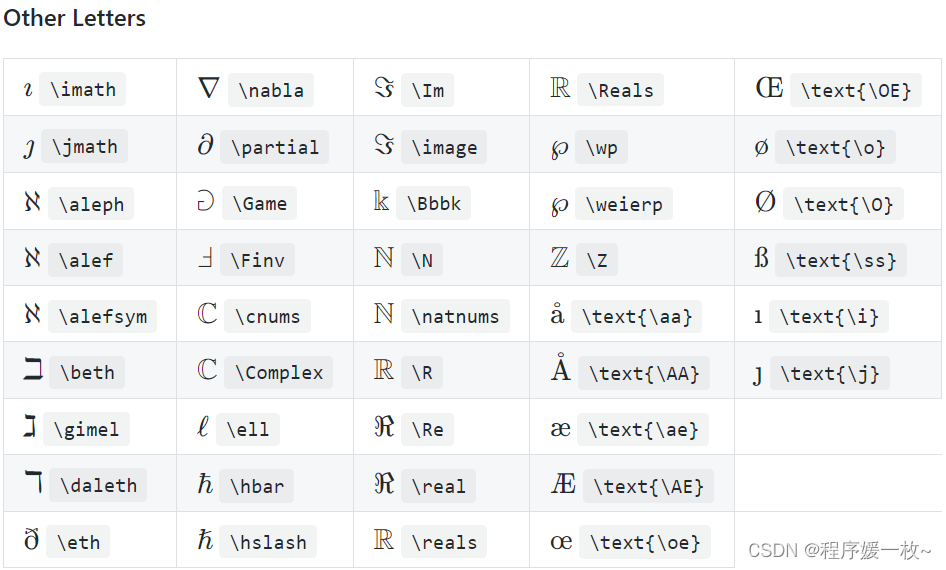
2.6 逻辑与集合论

2.7 大型符号

2.8 二进制符号

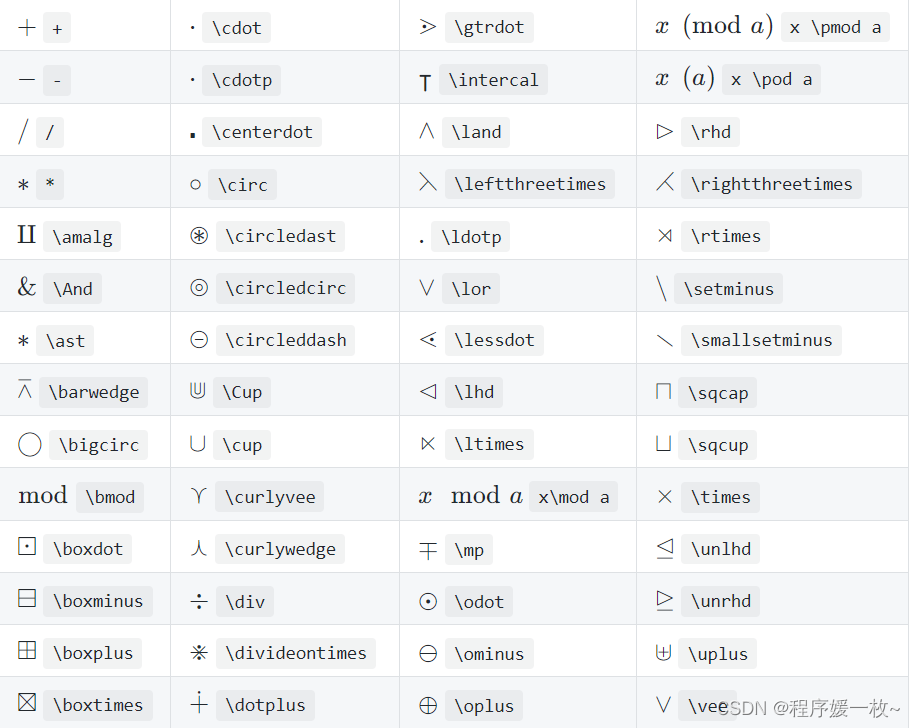
2.9 分数和二进制数

2.10 数学符号

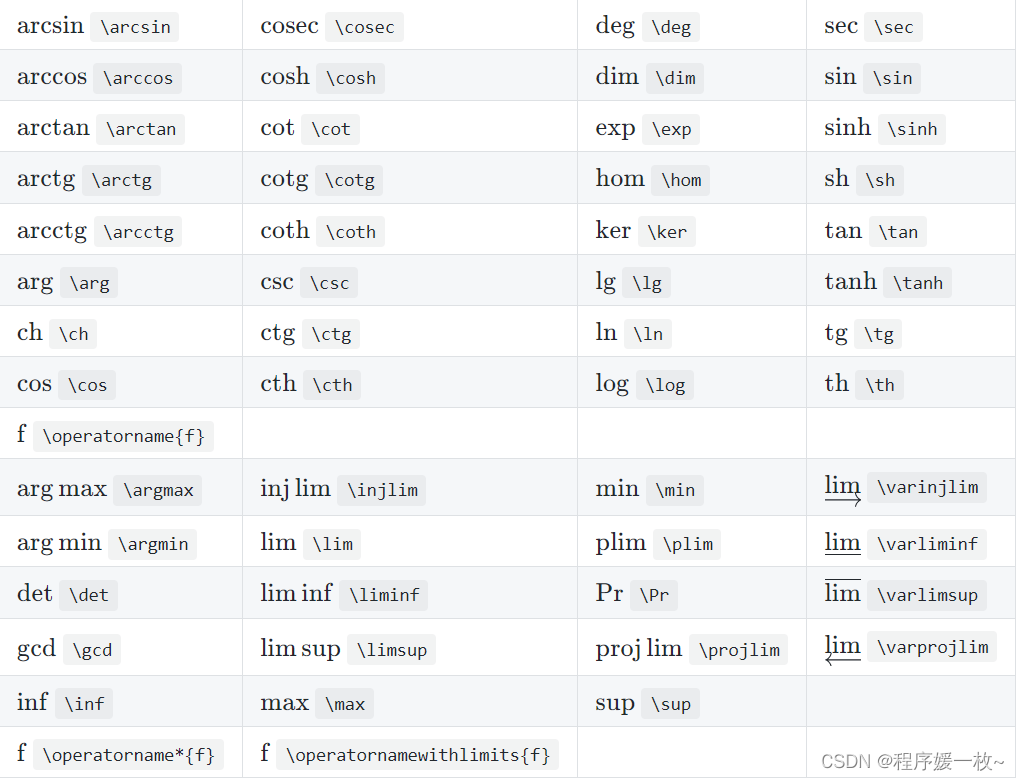
2.11 关系表达式

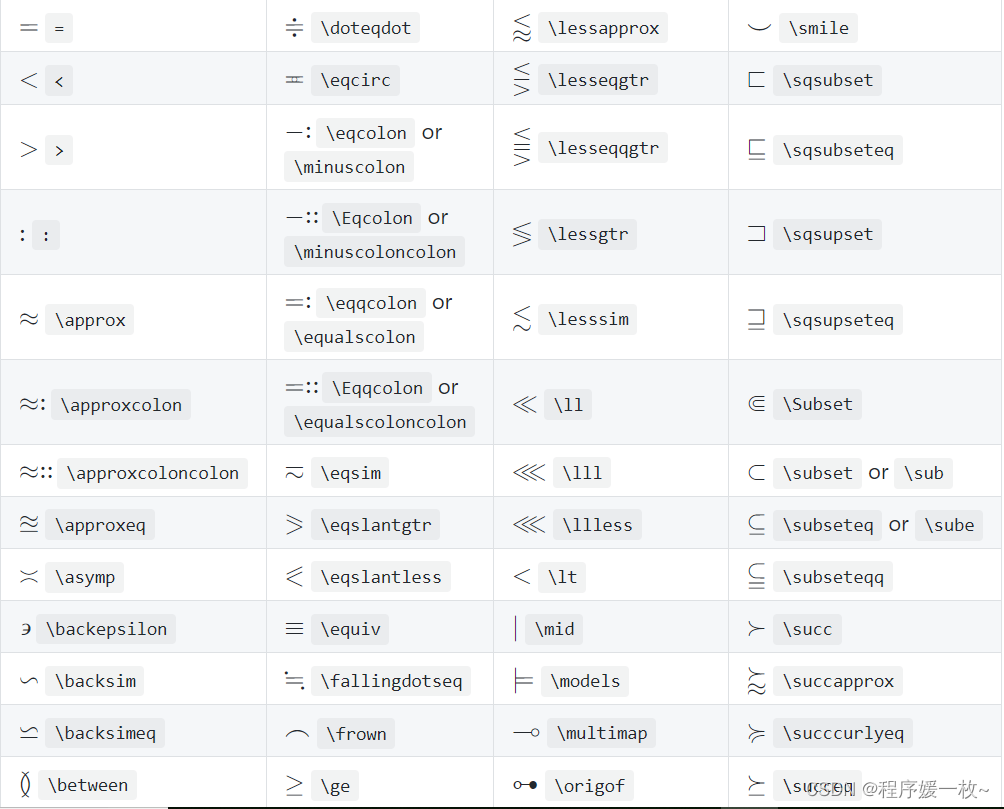
2.12 否定关系

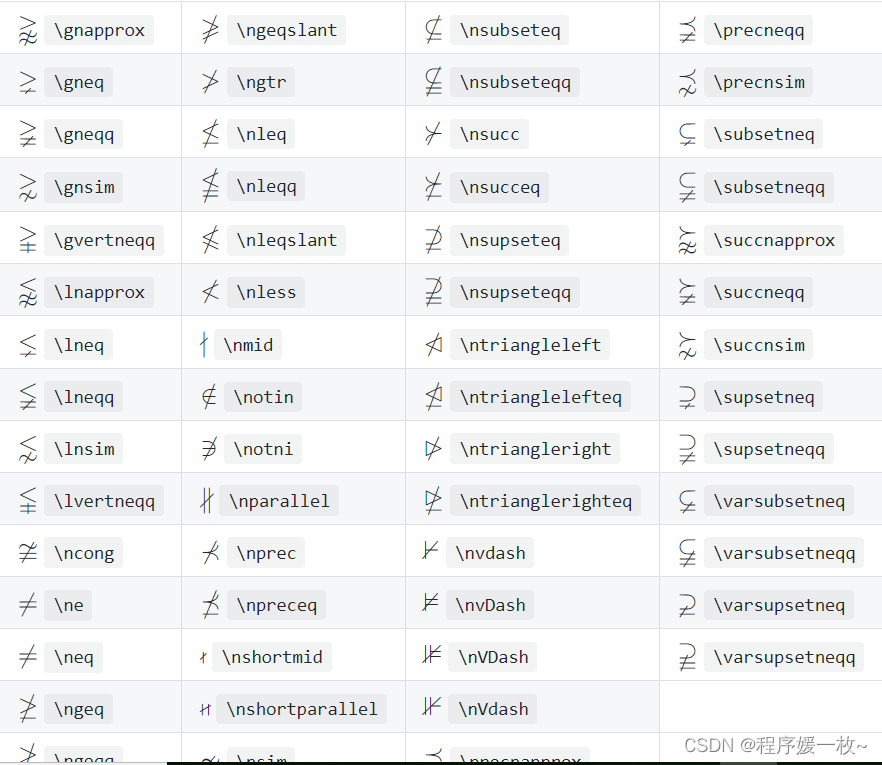
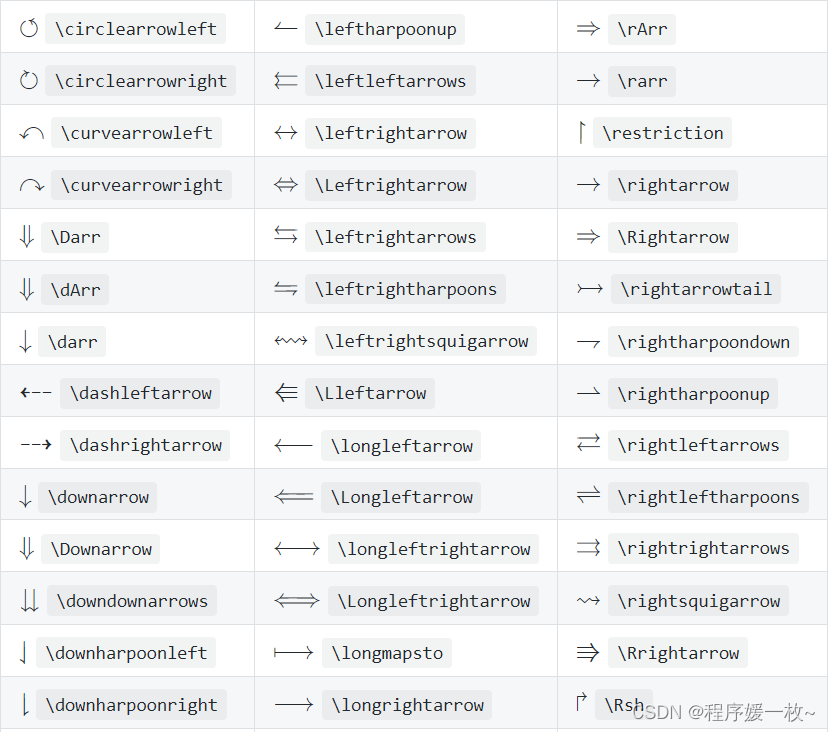
2.13 箭头 & 特殊箭头

2.14 颜色 加粗 斜体等也可

字体颜色：$$ \color{blue} F=ma $$
背景色：$$ \fcolorbox{red}{aqua}{$F=ma$} $$

不加粗：$${\sum_{\mathclap{1\le i\le j\le n}} x_{ij}} $$
加粗：整体公式加大括号，外加\bold
$$\bold {\sum_{\mathclap{1\le i\le j\le n}} x_{ij}} $$

字体颜色：$$F=ma$$
背景色：$$\boxed{F=ma}$$
不加粗：$$\sum _{1\le i\le j\le n}{x}_{ij}$$
加粗：$$\sum _{1\le \mathbf{i}\le \mathbf{j}\le \mathbf{n}}{\mathbf{x}}_{\mathbf{i}\mathbf{j}}$$

3. 源码

1. $$ E(T)=\sum_{(p,q)\epsilon\kappa} \mid\mid p-T_q \mid \mid ^2 $$
2. $$ E(T)=\sum_{(p,q)\epsilon\kappa} ((p-T_q) \cdot n_p)^2 $$
3. $$ \bold \tag{hi} x+y^{2x} $$
4. 不换行，只是显示为公式：$n_p$
5. 字体颜色：$$ \color{blue} F=ma $$
背景色：$$ \fcolorbox{red}{aqua}{$F=ma$} $$
不加粗：$${\sum_{\mathclap{1\le i\le j\le n}} x_{ij}} $$
加粗：$$\bold {\sum_{\mathclap{1\le i\le j\le n}} x_{ij}} $$
6. 下标：$$ ​ x_n $$
7. 上标：$$ e^x $$
8. $$​ a \atop b $$
9. $$ a\raisebox{0.25em}{$b$}c  $$
10. $$ \sum_{\mathclap{1\le i\le j\le n}} x_{ij} $$
11. $$ \begin{pmatrix}
   a & b \\
   c & d 
\end{pmatrix}	$$ 
12. $$	\begin{bmatrix}
   a & b \\
   c & d
\end{bmatrix} $$
13. $$
​	\begin{vmatrix}
   a & b \\
   c & d
\end{vmatrix}	$$
14. $$
​	\begin{Vmatrix}
   a & b \\
   c & d 
\end{Vmatrix} $$
15. $$ \begin{Bmatrix}
   a & b \\
   c & d
\end{Bmatrix}	$$
16. $$ \def\arraystretch{1.5}
   \begin{array}{c:c:c}
   a & b & c \\ \hline
   d & e & f \\
   \hdashline
   g & h & i
\end{array} $$
17. $$ x = \begin{cases}
   a &\text{if } b \\
   c &\text{if } d
\end{cases} $$

18. $$ \displaystyle\sum_{i=1}^n $$
19. $$ \textstyle\sum_{i=1}^n$$ 
20. $$ \lim\limits_x$$ 
21. $$ \lim\nolimits_x$$ 
22. $$ \verb!x^2!  $$

23. 符号
∑ \sum	∏∏ \prod	⨂⨂ \bigotimes	⋁⋁ \bigvee
∫∫ \int	∐∐ \coprod	⨁⨁ \bigoplus	⋀⋀ \bigwedge
∬∬ \iint	∫∫ \intop	⨀⨀ \bigodot	⋂⋂ \bigcap
∭∭ \iiint	∫∫ \smallint	⨄⨄ \biguplus	⋃⋃ \bigcup
∮∮ \oint	∯∬ \oiint	∰∭ \oiiint	⨆⨆ \bigsqcup

24. 希腊字母
A \Alpha	BB \Beta	ΓΓ \Gamma	ΔΔ \Delta
EE \Epsilon	ZZ \Zeta	HH \Eta	ΘΘ \Theta
II \Iota	KK \Kappa	ΛΛ \Lambda	MM \Mu
NN \Nu	ΞΞ \Xi	OO \Omicron	ΠΠ \Pi
PP \Rho	ΣΣ \Sigma	TT \Tau	ΥΥ \Upsilon
ΦΦ \Phi	XX \Chi	ΨΨ \Psi	ΩΩ \Omega
ΓΓ \varGamma	ΔΔ \varDelta	ΘΘ \varTheta	ΛΛ \varLambda
ΞΞ \varXi	ΠΠ \varPi	ΣΣ \varSigma	ΥΥ \varUpsilon
ΦΦ \varPhi	ΨΨ \varPsi	ΩΩ \varOmega	
αα \alpha	ββ \beta	γγ \gamma	δδ \delta
ϵϵ \epsilon	ζζ \zeta	ηη \eta	θθ \theta
ιι \iota	κκ \kappa	λλ \lambda	μμ \mu
νν \nu	ξξ \xi	οο \omicron	ππ \pi
ρρ \rho	σσ \sigma	ττ \tau	υυ \upsilon
ϕϕ \phi	χχ \chi	ψψ \psi	ωω \omega
εε \varepsilon	ϰϰ \varkappa	ϑϑ \vartheta	ϑϑ \thetasym
ϖϖ \varpi	ϱϱ \varrho	ςς \varsigma	φφ \varphi
ϝϝ \digamma

参考

• https://katex.org/docs/supported.html