两个数组的dp问题(1)--动态规划

一)最长公共子序列:

1143. 最长公共子序列 - 力扣（LeetCode）

一)定义一个状态表示:根据经验+题目要求

1)选取第一个字符串[0，i]区间以及第二个字符串[0，j]区间作为研究对象，先选取两段区间研究问题，先求出[0，i]中所有的子序列和[0，j]中所有的子序列，然后求出两个子序列中相同的最大的哪一个，找到最长公共子序列的长度；

2)根据题目要求来确定一个状态表示

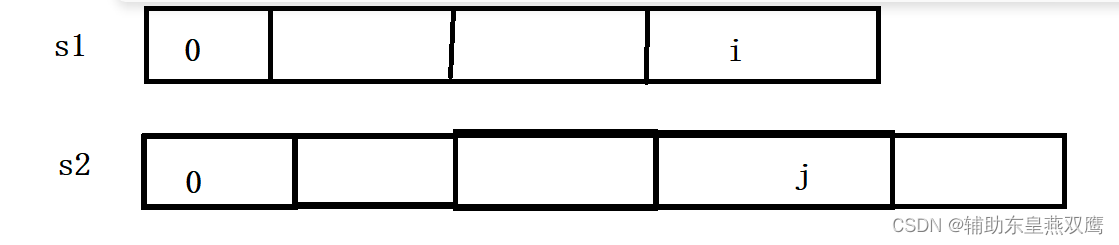
dp[i][j]就表示s1字符串的[0，i]区间以及s2的[0，j]区间内的所有子序列中(可以包含包含以i，j为结尾，也可以不包含i，j)，找到其中的最长的公共子序列的长度

二)根据状态表示推导状态转移方程:根据最后一个位置的状况来进行划分情况去讨论

如果这两个字符串的最后一个位置的字符相等，那么这两个字符串的最长公共子序列，一定是一这两个字符为结尾的，下面是用反证法来进行证明一下:

所以就可以根据这个最后一个字符的状态，分类讨论:

1)if(s1[i]==s2[j]) dp[i][j]=dp[i-1][j-1]+1

2)如果这两个字符不相等，那么最长公共子序列一定不是以这两个字符结尾的

s1[0，i]和s2[0，j-1]

s1[0，i-1]，s2[0，j]

s1[0，i-1]和s2[0，j-1]

但是仔细分析之后我们发现，第一种情况已经包含了第三种情况，第二种情况也是已经包含了第三种情况，但是我们此时求的是长度，只需要保证不漏就可以了，如果求的是个数，那么这个状态表示就出现问题了
三)初始化:

1)关于字符串的dp问题，空字符串是有研究意义的，子序列是一个空串那么也是一个公共子序列，引入空串的概念，会方便初始化

2)当i==0或者是j==0的时候，也就是当进行研究第一个字符的时候，dp[i-1]和dp[j-1]会越界，在上面和右边多增加一列，这时，当i==0的时候，第一个字符串是空，当j==0的时候，第二个字符串是空，此时dp表新增加的列里面的值全部是初始化成0；

3)添加辅助节点的时候，里面的值要保证我们后续进行填表的时候是正确的，还需要注意下标的映射关系，可以不在填表的时候进行处理，而是可以在所有的字符串前面加上一个空串，这样就可以不用计算下标的映射关系了

四)填表顺序+返回值:从上向下填写每一行，每一行填写从左向右dp[m][n]
class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
    int m=text1.length();
    int n=text2.length();
    char[] array1=text1.toCharArray();
    char[] array2=text2.toCharArray();
    int[][] dp=new int[m+1][n+1];
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            if(array1[i-1]==array2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
            else  dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
        }
    }
  return dp[m][n];
    }
}

二)不相交的线

求的是最长公共子序列

1035. 不相交的线 - 力扣（LeetCode）

dp[i][j]表示n1里面的[0,i]区间内以及n2里面的[0,j]区间内的所有子序列中，数组最长公共子序列的长度
class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int m=nums1.length;
        int n=nums2.length;
        int[][] dp=new int[m+1][n+1];
        for(int i=1;i<=m;i++){
             for(int j=1;j<=n;j++){
                 if(nums1[i-1]==nums2[j-1]){
                     dp[i][j]=dp[i-1][j-1]+1;
                 }else{
                     dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                 }
            }
        }
    return dp[m][n];
    }
}

三)不同的子序列

115. 不同的子序列 - 力扣（LeetCode）

一)定义一个状态表示:

两个字符串的dp表示:dp[i][j]表示从[0，i]位置的t子串在s从[0，j]的子序列中出现的个数

dp[i][j]表示s字符串[0，j]区间内的所有子序列中，有多少个t[0，i]区间内的子串，子串是连续的，但是子序列是不连续的

二)根据状态表示推导状态转移方程:

1)我们可以将s从[0，j]这段字符串的子序列分成两类，就是根据最后一个位置的元素进行划分问题，我们目标是在s的子序列中看看有多少个t字符串

首先求出所有子序列，在求出有多少子序列中等于t

2)可以根据s的子序列中的最后一个位置是否包含j来进行划分问题，s的子序列分成两类

2.1)如果s的子序列中，最后一个位置包含s[j]，if(array[i]==array[j]) dp[i][j]=dp[i-1][j-1]

2.2)如果s的子序列中，最后一个位置不包含s[j]，dp[i][j]=dp[i][j-1]

我们要找的是[0，i]位置的子串在[0，j]区间内的子序列出现的个数

dp[i][j]就是上面两种情况的的总和

三)初始化+填表顺序+返回值:

3.1)因为有可能使用到i-1和j-1的值，那么我们给dp表新增加一行和一列

3.2)我们下标从1位置和1位置开始，也就是从第一个字符开始进行研究问题

3.3)细节问题:

1)引入空串

2)保证里面的值要保证后面的填表的顺序是正确的

3)还需要注意下表的映射关系:不做任何处理只是在进行填写dp表的时候下标统一进行-1即可

或者是加上在原来的字符串里面加上一个空字符即可

4)当i等于0的时候，说明t字符串是一个空串，那么无论此时j的值等于多少，s的子序列中一定是包含一个空串的，那么所有的dp[0][j]=1

5)那么当j等于0的时候，说明s没有任何子序列，s是一个空串，那么除了i等于0的时候

dp[i][0]都等于0，当i==1的时候，dp[i][0]=1

初始化:从上向下填写每一行，每一行从左向右

返回值:dp[m][n]
class Solution {
    public int numDistinct(String s, String t) {
        char[] array1=t.toCharArray();
        char[] array2=s.toCharArray();
        int[][] dp=new int[array1.length+1][array2.length+1];
        for(int i=0;i<=array2.length;i++){
           dp[0][i]=1;
        }
        for(int j=1;j<=array1.length;j++){
            dp[j][0]=0;
        }
    for(int i=1;i<=array1.length;i++){
        for(int j=1;j<=array2.length;j++){
//1.如果以j为结尾的子序列包含j,况且array1[i]==array2[j]
            if(array1[i-1]==array2[j-1]){
                dp[i][j]=dp[i-1][j-1];
            }
//2.如果以j为结尾的子序列不包含j,
             dp[i][j]+=dp[i][j-1];
        }
    }
    System.out.println(Arrays.deepToString(dp));
  return  dp[array1.length][array2.length];
    }
}

四)通配符匹配

44. 通配符匹配 - 力扣（LeetCode）

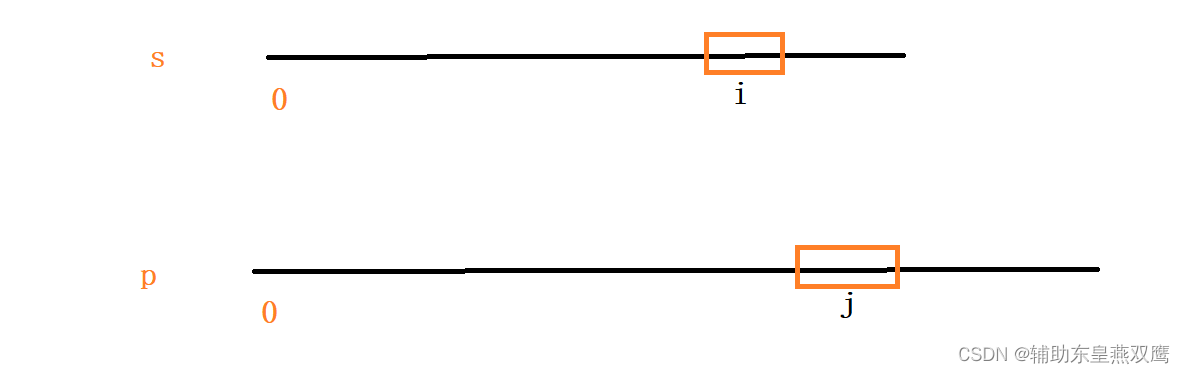
我们进行研究的是p这个字符串是否能够匹配s，我们先进行选取s字符串的[0，i]区间，再进行选取p字符串的[0，j]区间，先进行研究p的[0，j]的区间是否能匹配s字符串的[0，i]区间

一)定义一个状态表示:

dp[i][j]表示p[0，j]这段区间内字符串的子串能否匹配s区间内[0，i]的子串

二)根据状态表示推到状态转移方程:根据最后一个位置的状况来进行划分问题

我们这个dp[i][j]就可以p根据最后一个位置的情况来进行划分问题

1)如果p这个字符串的最后一个位置是普通字符，不是*也不是?，此时如果说要相匹配成功，需要满足s[i]=p[j]，同时还需要满足dp[i-1][j-1]是true，因为还要满足p[0，j-1]区间要能够匹配s[0，i-1]区间内的子串；

2)p[j]如果是等于字符?，?只能匹配一个字符，但是此时这个?只能干掉最后一个字符，那么此时我们还是需要进行判断p[0，j-1]区间要能够匹配s[0，i-1]区间内的子串；

3)如果p[j]是一个*，这个*可以匹配空字符串，可以匹配一个字符，可以匹配多个字符，如果3.1)这个*匹配的是一个空串那么我们需要检查p[0，j-1]区间是否能够匹配s[0，i]区间内的字符串

3.2)如果p[j]这个字符匹配的是一个字符，我们此时还是需要看s字符串[0，i-1]的字符是否能够被p字符串[0，j-1]的字符串匹配

3.3)如果这个p[j]这个字符能够匹配两个字符，那么此时就需要检查s字符串[0，i-2]内的字符是否能够被p字符串[0，j-1]的字符串匹配

等等等我们的这个p[j]字符时还是可以匹配三个字符，四个字符等等等dp[i-k][j-1]k是*能够匹配的字符个数，在这里面我们还需要使用循环来进行判断，况且只是需要满足一种情况即可，此时的时间复杂度已经达到了O(N^3)，况且只需要满足一种情况即可，如果填写二维dp表的时候，时间复杂度已经达到了O(N^3)此时就需要采取优化的手段了，但是这些状态是否能由若干个有限的状态表示

4)优化:前提是p[j]=="*"

优化1:

dp[i][j]=dp[i-1][j-1]||dp[i-2][j-1]||dp[i-3][j-1].....

dp[i-1][j]=dp[i-2][j-1]||dp[i-3][j-1]....

那么此时dp[i][j]就可以优化成dp[i-1][j]||dp[i-1][j-1]

优化2:根据状态标识以及实际情况来优化状态转移方程

当p[j]=="*"的时候，那么可以匹配的情况分成两种:

1)当进行匹配空字符串的时候，那么dp[i][j]=dp[i][j-1]，相当于"*"白用了

2)第二种情况就是不让这个p[j]匹配单个字符串了，只是让p[j]匹配一个字符串，但是这个p[j]的子字符串还不会进行丢弃，然后继续看[0，j]这个区间能否匹配[0，i-1]这个区间

所以sp[i][j]=dp[i][j-1]||dp[i-1][j]

三)初始化:

当有字符串需要进行初始化的时候是需要有三个细节问题需要进行考虑的

1)引入空串的概念:在原始的dp表里面最上面加上一行，在最左边加上一列，让第一行表示第一个字符串是空的情况，让第一列表示第二个字符串是空的情况，让原来的dp表统一向右下移动一位

1.1)当我们的s字符串是空的时候，p字符串时空串的时候能够进行匹配空串，或者是"*"字符串的时候能够匹配空串，如果全都是连续的*就可以进行匹配，如果遇到的不是"*"直接返回，如果*是不连续的，那么全部是false

1.2)如果p是空串，那么s如果不时空串，那么就是false

2)里面的值要保证后续的填表是正确的

3)下标的映射关系:一般是在两个字符串前面加上一个空串，要么就是采用下标-1的方式

四)填表顺序:从上向下填写每一行，每一行从左向右

五)返回值:dp[m][n]

不优化:是时间复杂度是O(N^3)

class Solution {
    public boolean isMatch(String s, String p) {
        char[] array1=s.toCharArray();//被匹配的0-i
        char[] array2=p.toCharArray();//要匹配的0-j
        boolean[][] dp=new boolean[array1.length+1][array2.length+1];
        dp[0][0]=true;//空字符串匹配空字符串是一定可以匹配成功的
        for(int i=1;i<=array2.length;i++){
//如果遇到了某一个字符是"*"一定可以匹配成功空串,如果遇到的不是*那么当前以及后面都无法匹配成功
            if(array2[i-1]=='*') dp[0][i]=true;
            else break;
        }
        for(int i=1;i<=array1.length;i++){
            for(int j=1;j<=array2.length;j++){
        if(array2[j-1]!='?'&&array2[j-1]!='*'){
          if(array1[i-1]==array2[j-1]){
                    dp[i][j]=dp[i-1][j-1];
           }else{
               dp[i][j]=false;
           }
               }else if(array2[j-1]=='?'){
                    dp[i][j]=dp[i-1][j-1];
               }else{
                   for(int k=0;k<=i;k++){
                      if(dp[k][j-1]==true){
                          dp[i][j]=true;
                          break;
                      }
                   }
               }
            }
        }
    return dp[array1.length][array2.length];
    }
}

优化时间复杂度:O(N^2)

五)最长公共前缀:

一)定义一个状态表示:dp[i]表示以i位置为结尾的字符串数组的最长公共前缀

二)根据状态表示状态转移方程:

1)根据最近的一步来进行划分问题，如果发现这个字符串所有的i位置的元素都是相等的，那么最长公共前缀就是dp[i-1]+"ch"，但是如果出现了abcde和hhhhe这种情况，如果发现以i-1位置为结尾的最长公共公共前缀是空，那么dp[i]也是空，虽然相等但是没有最长公共前缀

2)如果发现各个字符串在i位置的元素不是全部都相等，那么直接返回dp[i-1]的值
class Solution {
    public String longestCommonPrefix(String[] strs) {
        //dp[i]表示以i位置为结尾字符串数组的最长公共前缀
        String minString=strs[0];
        for(String str:strs){
            if(minString.length()>=str.length()) 
              minString=str;
        }
        if(minString.equals("")) return "";
//1.先进行初始化
       String[] dp=new String[minString.length()];
       char ch=strs[0].charAt(0);
       dp[0]=ch+"";
       for(String str:strs){
           if(str.charAt(0)!=ch){
               dp[0]="";
               break;
           }
       }
//2.进行填表
     for(int i=1;i<minString.length();i++){
           ch=minString.charAt(i);
          for(int j=0;j<strs.length;j++){
              if(strs[j].charAt(i)!=ch){
                return dp[i-1];
              }
          }
        if(!dp[i-1].equals("")) dp[i]=dp[i-1]+ch;
        else dp[i]="";
      }
    return dp[minString.length()-1];
    }
}

六)正则表达式匹配

10. 正则表达式匹配 - 力扣（LeetCode）

1)* 匹配零个或多个前面的那一个元素，这句话的意思就是*和某一个字符组合，这个字符可以出现0次，也可以出现1次，也可以出现两次，也可以出现N次

a*可以匹配空串，可以匹配aa，aaa，aaaa，aaaa，就是可以把*a变换成上面的值

2).*可以匹配成空串，一个.，两个.，三个.，或者是若干个.，所以.*可以匹配任何字符串

3)s="aab"，p="d*a*."，d*可以匹配一个空串，a*可以匹配aa剩下的一个.可以匹配b字符串

4)保证每次出现字符 * 时，前面都匹配到有效的字符，也就是说当某一个位置是*的时候，前面的字符都是能够进行匹配的有效字符，也就是a-z或者是.，绝对不可能出现*字符，也就是两个**是不能连着的

一)确定一个状态表示:

dp[i][j]表示从s[0，i]这个字符串，能否被p这个字符串从[0，j]进行匹配

dp[i][j]表示p这个字符串[0，j]区间内的子串是否能够匹配s[0，i]区间内的子串

二)根据状态表示来推导状态转移方程:这个状态转移方程的推导，仍然是根据最后一个位置的状况来进行划分问题来进行分情况讨论

我们还是和上个题一样，从p这个字符串的最后一个位置来进行划分问题:

1)如果p[j]是一个普通字符(a-z)，那么如果s子串如果想要和p字符子串进行匹配，那么p[j]必须等于s[i]，if(p[j]==s[j]) dp[i][j]=dp[i-1][j-1]，如果这两种情况有一种条件不满足，那么就直接返回false

2)如果p[j]是一个.，那么这个字符也是可以只干掉一个字符，那么dp[i][j]=dp[i-1][j-1]

3)如果p[j]是一个"*"那么p[j]必须和前面的一个字符进行匹配

3.1)如果说p[j]的字符是一个"*",那么这个字符必须得和前面的字符搭配在一起进行使用,单独进行使用是没有任何意义的
3.2)如果前一个字符是"."的话,那么这个字符串可以翻译成空串,可以翻译成一个.，可以翻译成两个..,可以翻译成三个.
a)如果".*"相进行结合翻译成"",那么dp[i][j]=dp[i][j-2]
b)如果".*"进行相结合翻译成一个.".",那么这个.是可以进行匹配s字符串中的一个字符

dp[i][j]=dp[i-1][j-2]
c)如果".*"进行相结合翻译成两个."..",那么是可以进行匹配s字符串中的两个字符的

dp[i][j]=dp[i-2][j-2]，等等等等，在上面的情况中只要有一个true，那么整个的结果dp[i][j]的结果就是true，在这里面我们再来分析一下时间复杂度已经达到了O(N^3)，能不能采取以下优化手段呢？

3.3)

a)优化方式:使用数学的方式来进行优化

dp[i][j]=dp[i][j-2]||dp[i-1][j-2]||dp[i-2][j-2]

dp[i-1][j]=dp[i-1][j-2]||dp[i-2][j-2].....

dp[i][j]=dp[i][j-2]||dp[i-1][j-2]

b)根据状态标识以及结合实际情况来进行分析状态转移方程

当".*"进行匹配空串的时候，dp[i][j]=dp[i][j-2]

当".*"进行匹配一个字符串的时候，不会将这两个字符舍去，而是让p字符串[0,j]继续去匹配s[0，i-1]位置的子串，dp[i][j]=dp[i-1][j-2]，这两种情况只需要有一种情况满足就可以了

3.4)如果p[j]是一个"*"，而p[j-1]是一个普通字符(a-z)

a)如果我去匹配一个空串，那么dp[i][j]=dp[i-1][j-2]

b)如果匹配的不是空串，如果是普通字符+"*"

匹配一个字符，p[j-1]=s[i]&&dp[i][j]=dp[i-1][j-2]

匹配两个相同的字符，p[j-1]=s[i]=s[i-1]，dp[i][j]=dp[i-2][j-2]

匹配k个相同的字符，p[j-1]=s[i]=.....=s[i-k]，dp[i][j]=dp[i-k][j-2]

但是这里面又是可以做优化的:dp[i][j]=dp[i-1][j]，只是匹配一个字符然后进行保留