基于密度的噪声应用空间聚类(DBSCAN)是一种无监督聚类算法,它可以替代KMeans和层次聚类等流行的聚类算法。
KMeans 的缺点
- 容易受到异常值的影响,离群值对质心的移动方式有显著的影响。
- 在集群大小和密度不同的情况下存在数据精确聚类的问题。
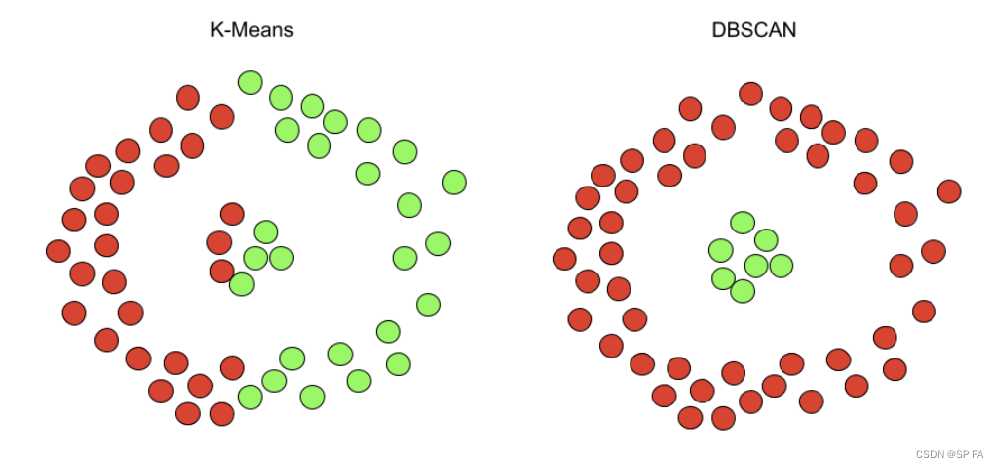
- 只能应用于球形簇,如果数据不是球形的,它的准确性就会受到影响。
- KMeans 要求我们首先选择希望找到的集群的数量,无法自动判断集群的类别。
针对这些缺点,人们提出了 DBSCAN 算法
1. 算法流程
首先该算法用到两个参数:
eps:领域半径min_samples:领域半径内的最少点数
还有一些基本概念:
- 核心点:算法会遍历每一个点,并统计以该点为圆心,半径为
eps的圆内点的数量,如果大于等于min_samples,那么该店就是核心点 - 密度直达:如果点
P
P
P 为核心点,点
Q
Q
Q 在
P
P
P 的邻域内,也就是它们间距离小于
eps,那么 P P P 到 Q Q Q 密度直达。注意,密度直达不具有对称性,也就是 P P P 到 Q Q Q 密度直达, Q Q Q 到 P P P 不一定密度直达,因为 Q Q Q 可能不是核心点。 - 密度可达:如果有这么一组核心点: { P i ∣ 0 ≤ i ≤ n } \{P_i~|~0\le i\le n\} {Pi ∣ 0≤i≤n},并且 P i P_i Pi 到 P i + 1 P_{i+1} Pi+1 密度直达, P n P_n Pn 到 Q Q Q 密度直达且 P 1 P_1 P1 到 Q Q Q 不是密度直达,那么 P 1 P_1 P1 到 Q Q Q 密度可达。密度可达也不具有对称性
- 密度相连:如果存在核心点 S S S,使得 S S S 到 P P P 和 Q Q Q 都密度可达,则 P P P 和 Q Q Q 密度相连。密度相连具有对称性,如果 P P P 和 Q Q Q 密度相连,那么 Q Q Q 和 P P P 也一定密度相连。密度相连的两个点属于同一个聚类簇。
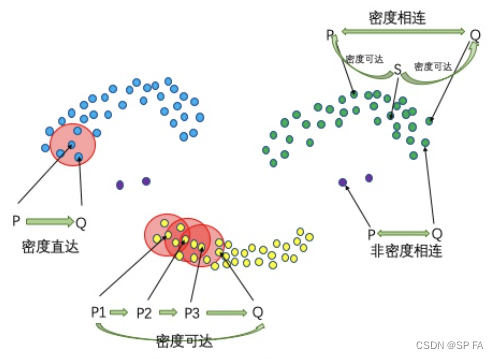
看完上面的这些概念,对于这个算法的流程可能就已经有些眉目了,该算法的步骤可以大概分为两部分:
- 遍历没有访问过的点,并且找到一个核心点 P P P,归为类别 i i i
- 从这个核心点开始往外扩展:把它的密度直达点放到集合 Q = { q j } Q=\{q_j\} Q={qj},依次遍历集合内所有点 q j q_j qj,统统归为类别 i i i,再判断一下 q j q_j qj 是不是核心点,如果是的话继续从 q j q_j qj 开始重复第二步,直到没有新的点加入集合 Q Q Q,并且这个集合内的点全被访问过。这样集合 Q Q Q 内的点全部都是密度相连的,并且它们统统都是类别 i i i,因此该算法是成立的。
2. 代码实现
又是喜闻乐见的展示代码环节
class DBSCAN:
def __init__(self, eps, min_samples):
self.distance = None
self.visit = None
self.label = None
self.eps = eps
self.min_samples = min_samples
def fit(self, X):
"""
分类 id 从 1 开始,0 为噪声
"""
self._distance(X)
n_samples = X.shape[0]
self.visit = np.zeros(n_samples)
self.label = np.zeros(n_samples)
clusterId = 1
for i in range(n_samples):
if self.visit[i] == 1:
continue
self.visit[i] = 1
neighbors = self._region_query(i)
if len(neighbors) < self.min_samples:
self.label[i] = 0 # 标记为噪声点
else:
self.label[i] = clusterId
self._expand_cluster(neighbors, clusterId)
clusterId += 1
self.label = self.label.astype(int)
return self.label
def _distance(self, X):
self.distance = np.linalg.norm(X[:, np.newaxis] - X, axis=-1)
def _region_query(self, i):
dists = self.distance[i]
neighbors = np.argwhere(dists <= self.eps).squeeze(axis=1)
return neighbors
def _expand_cluster(self, neighbors, clusterId):
j = 0
while j < len(neighbors):
neighbor = neighbors[j]
if self.visit[neighbor] == 0:
self.visit[neighbor] = 1
self.label[neighbor] = clusterId
new_neighbors = self._region_query(neighbor)
if len(new_neighbors) >= self.min_samples:
neighbors = np.concatenate((neighbors, new_neighbors), axis=0)
j += 1
测试代码
import numpy as np
import matplotlib.pyplot as plt
from draw_point import map_label_to_color
def generate_dataset(num_clusters, num_points_per_cluster, noise_ratio):
# 确定数据集的范围
x_range = (-10, 10)
y_range = (-10, 10)
# 生成聚类中心点
cluster_centers = []
for _ in range(num_clusters):
center_x = np.random.uniform(*x_range)
center_y = np.random.uniform(*y_range)
cluster_centers.append((center_x, center_y))
# 生成数据点
dataset = []
for center in cluster_centers:
points = []
for _ in range(num_points_per_cluster):
offset_x = np.random.uniform(-1, 1)
offset_y = np.random.uniform(-1, 1)
point_x = center[0] + offset_x
point_y = center[1] + offset_y
points.append((point_x, point_y))
dataset.extend(points)
# 生成噪声点
num_noise_points = int(len(dataset) * noise_ratio)
noise_points = []
for _ in range(num_noise_points):
noise_x = np.random.uniform(*x_range)
noise_y = np.random.uniform(*y_range)
noise_points.append((noise_x, noise_y))
dataset.extend(noise_points)
return np.array(dataset)
colorLst = [
(1, 0, 0), # 红色
(0, 1, 0), # 绿色
(0, 0, 1), # 蓝色
(1, 1, 0), # 黄色
(1, 0, 1), # 品红色
(0, 1, 1), # 青色
(0.5, 0, 0), # 深红色
(0, 0.5, 0), # 深绿色
(0, 0, 0.5), # 深蓝色
(0.5, 0.5, 0.5), # 灰色
(0, 0, 0) # 白色
]
# 生成数据集
num_clusters = 4
num_points_per_cluster = 50
noise_ratio = 0.1
dataset = generate_dataset(num_clusters, num_points_per_cluster, noise_ratio)
eps = 1
min_samples = 4
dbscan = DBSCAN(eps, min_samples)
labels = dbscan.fit(dataset)
labels = map_label_to_color(labels)
plt.scatter(dataset[:, 0], dataset[:, 1], s=5, c=[colorLst[i] for i in labels])
plt.title('DBSCAN Test Dataset')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
效果如下:
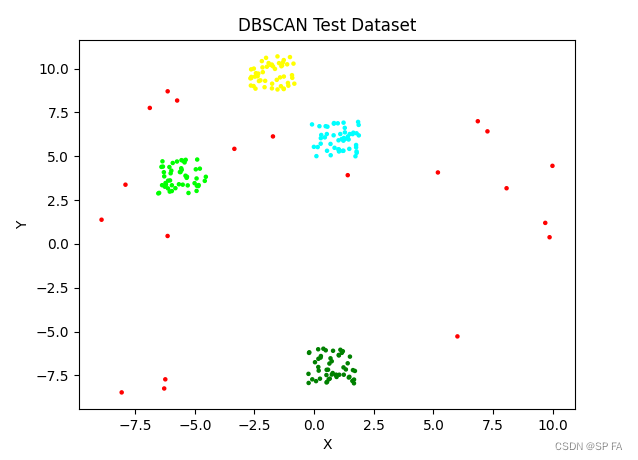
3. 确定参数
还记得 eps 和 min_samples 这两个参数吗,我们要想让算法有不错的效果,这个两个的值必须合适才可以。
min_samples的取值:很简单,2 * 维度 即可eps的取值:- 首先要选取一个 k 值,一般为 2 * 维度 - 1
- 计算并绘制 k-distance 图。即计算出每个点到距其第 k 近的点的距离,然后将这些距离排序后进行绘图。
- 找到拐点位置的距离,即为
eps的值。
这里我用的 KDTree 来快速找到第 k 近的点,代码如下,KDTree 的实现可以看我之前的博客:
import os
import numpy as np
import pandas as pd
from tqdm import tqdm
from model.kdTree import KDTree
from tools.visualization import draw_plots
csvPath = "./data/radar_3"
files = os.listdir(csvPath)
totDistLst = []
for i in tqdm(files):
df = pd.read_csv(os.path.join(csvPath, i))
points = np.array([df['u'].tolist(), df['v'].tolist(), df['z'].tolist()]).T
kdt = KDTree(points, 4)
for j in range(points.shape[0]):
points, dist = kdt.search_nearest(j, isInner=True)
totDist = -dist[0]
totDistLst.append(totDist)
totDistLst = sorted(totDistLst)
draw_plots("k-distance", totDistLst)
从下图可以看出,如果点的数量很多的话,拐点还是不太好确定的,可以通过分段的方式画出多个区间的图,再去具体的判断 eps 取值,比如在这个整体的图上看感觉拐点是在 250 的位置,但是如果把所有的点分成几部分分开来看的话,会发现取 50 左右才是最合适的值。