嬴图 | K邻算法在风险传导场景中的实践意义

随着图思维方式与图数据框架在工业领域的有效开展和深入应用，可靠且高效的图算法也就成为了图数据探索、挖掘与应用的基石。该图算法系列（具体见推荐阅读），集合了 Ultipa 嬴图团队在算法实践应用中的经验与思考，希望在促进业界爱好者交流的同时，能从技术层面为企业的图数据库选型开拓一些思路。

K邻（K-Hop Neighbor）即K跳邻居，是基于广度优先（BFS）[1] 的遍历方式对起始节点周边的邻域进行探索的一种算法，广泛应用于关系发现、影响力预测、好友推荐等预测类场景。

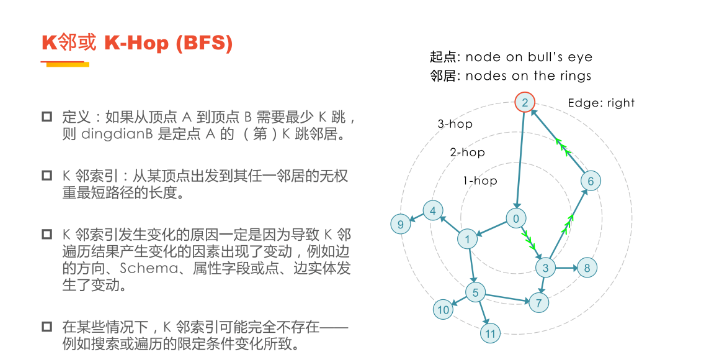
在图论中，沿着一条边游走一个单位路径被称之为一跳（hop）。遍历图中的顶点时，就会涉及到多跳的问题。

图论最早脱胎于数学家欧拉于 1836 年提出的哥尼斯堡七桥问题，它是图计算的数学基础，从上世纪 80 年代开始，图计算得到了快速的发展。

在真实世界中，危机的传递就是典型的K邻搜索的过程，以发生危机的实体为起点[2] ，顺着或逆着（取决于边的具体定义）边[3]的方向进行1步、2步、3步直至更深的查询，得到的就是先后会被危机波及到的实体。

我们以某著名房地产企业HD的供应链图谱为例，看看如何在图上通过持股方向、资金流向等，清晰直观地反映出危机的传递方向以及传递对象。

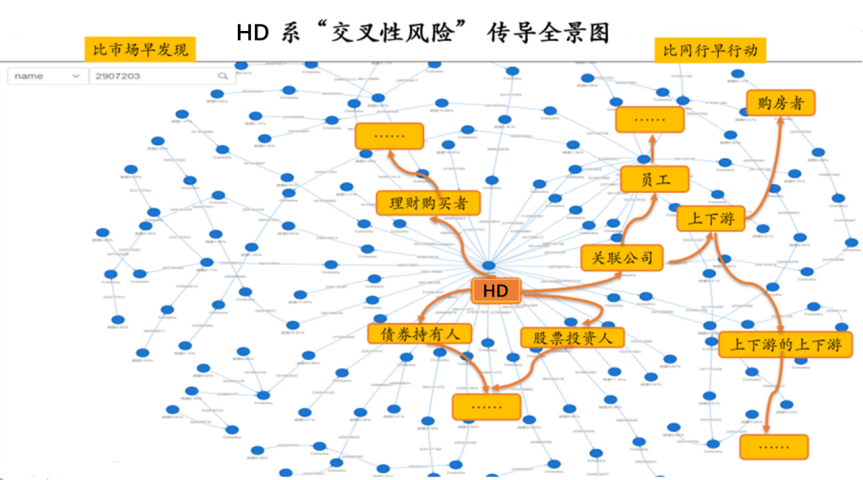
以HD为例，其发生危机后，风险的传播路径为：

·第一层：传播到HD的关联公司；
·第二层：传播到公司员工和供应商；
·第三层：传播到购房者：供应商停止供货、工人拒绝复工，HD的在建工程就可能烂尾）

……以此类推，风险从最初的HD集团一个点最后传播到关联公司、员工、供应商、购房者等，形成一张“网络”，风险是一层一层传播的——“链条效应”明显。【关于图技术在风险管理领域的详细阅读，参阅：图计算在交叉性金融风险管理的创新】

而事实上，很多与传导相关的实际应用并不是基于图计算进行的，而是用纯手工计算来完成的。

如很多银行的KYC（Know Your Client）部门在计算其对公客户的UBO（Ultimate Beneficial Owner，最终受益人）时，仍在使用Excel表进行计算——可想而知这样的计算效率和准确率有多低。

显然，这和很多金融机构的IT系统陈旧、工作方法落伍有着直接关系，并将阻碍这些机构的业务开展，例如客户的企业影响力分析。我们知道，企业影响力分析的内容，远不止探讨持股关系、生产供求关系等传统的问题，凡是和企业相关的金融行为、事件，以及与这些事件行为有直接关联、甚至间接关联的事务，都应被列在研究范围内。同时，分析的出发点不应该只局限于一个企业实体，而应该扩展延伸至企业发布的产品、债券……

如图3所示，分析的核心为一家企业的某个债券，该债券价格的下跌可能直接影响该企业发布的其他债券的价格：

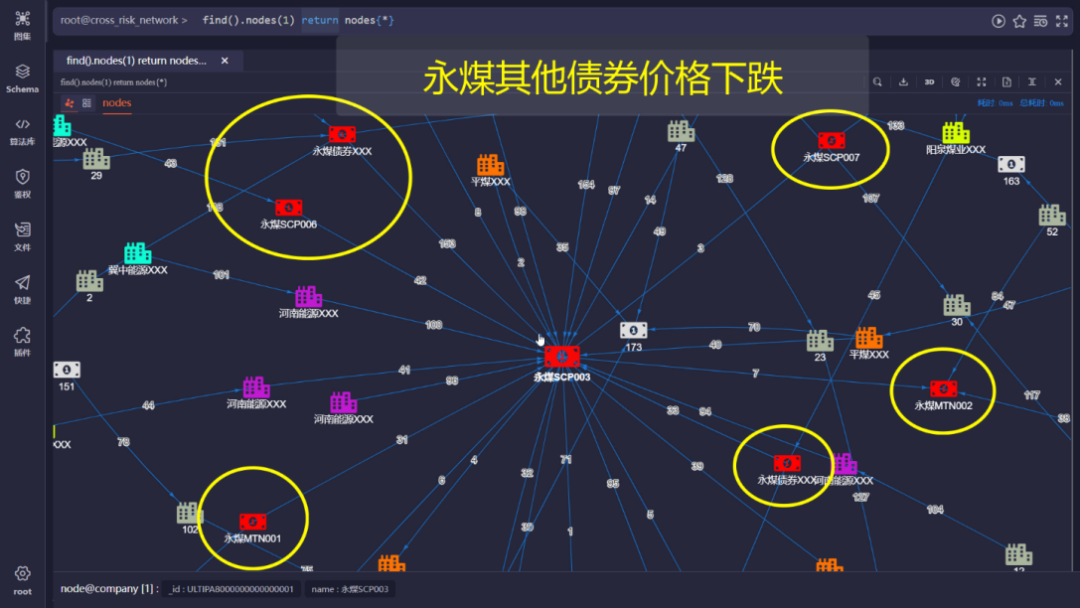
图4标出的则为持有该债券的、可能被影响到的省内其他企业：

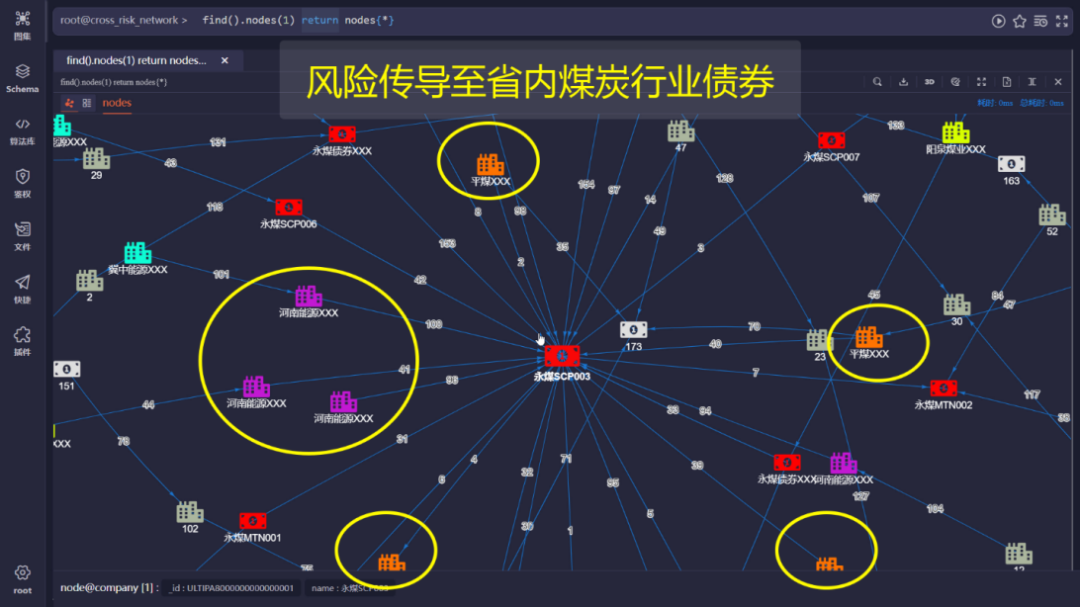
图3、图4所示的均为该债券的1步邻居，从这些邻居继续向外探寻就能得到该债券价格下跌后产生的危机传递效应，如图5所示：

专家们已越来越认识到，金融风险并不是孤立存在的，不同风险间具有链条效应，任何一只蝴蝶扇动翅膀，都有可能造成跨市场的风险传染——风险的关联性具有相互转化、传递和耦合的特点。图技术与蝴蝶效应在本质上是不谋而合的，即通过深度挖掘不同来源的数据，以网络化分析的方式去洞察。【更多阅读，链接：图计算引发银行流动性风险管理变革】

此外，金融场景是一种基于长链条计算的场景，这就导致技术实现时的规则更为复杂，因为会涉及到各种回溯、归因，而且数据的计算量更大，同时也更注重时效性。只有实现真正的实时、全面、深度穿透、逐笔追溯、精准计量的监测和预警，才能保障金融风控中避免出现“蝴蝶效应”式的风险的发生。【更多阅读，链接：沸点·专访 | 科技赋能银行流动性风险管理的“AI路径”| 沸点 & 伦敦流动性管理会议 Ultipa亮相】

值得注意的是，图往往包含着复杂的属性及定义，例如：边的有向、无向，边的属性权重，K 邻是否包含 K-1 邻，如何处理计算环路等等，这些问题会导致 K 邻算法具体实现的差异。此外，在一些实际场景中，图自身拓扑结构的变化，过滤条件的设定，节点、边属性的变化都会影响到 K 邻计算的结果。【更多阅读，链接：图数据库查询与算法正确性验证】

此外，K邻算法在行业中的应用，多为多模态的异构图，就是将很多张信息单一的图融合在一起的综合性的图谱。这不仅对算法实现相关人员的数据收集能力、构图能力提出了非常高的要求，也对K邻算法在灵活性、功能性等方面是否满足业务需求提出了更高的要求。【Ultipa 嬴图的高密度并发图算法是目前全球运行最快、最丰富（超过100+）的图算法库的集合，可通过 EXTA 接口热插拔和扩展。】

如果你在很多公开的资料中，看到很多关于K邻应用的例子都是同构图（只有一种点、一种边），那么多半是以下情况：

· 作者想通过简单的例子来阐明观点，如社交网好友推荐的应用场景

· 构图能力不足，从而限制了算法的使用

· K邻算法的实现不尽人意，无法对异构图进行恰当处理

K邻的应用应该是广泛的，实际的，能解决现实问题的，如果是因为后面两种情况而限制了算法的“大展宏图”，那么相关图厂商就应该反思一二并提高自身了！

值得一提的是，一个算法设计的好坏，除了具备解决问题的能力，还需要关注计算的效率，也就是算力。在最后，我们列举出一些高性能的图计算（图数据库）系统应具备的核心能力，以供企业在甄别市场上林林总总的图计算产品时进行参考：

·高速图搜索能力：高QPS/TPS、低延时，实时动态剪枝（过滤）能力

·对任何规模的图的深度、实时搜索与遍历能力（10层以上）

·高密度、高并发图计算引擎：极高的吞吐率

·成熟稳定的图数据库、图计算与存储引擎、图中台等

·可扩展的计算能力：支持垂直与线性可扩展

·3D+2D高维可视化、高性能的知识图谱Web前端系统

·便捷、低成本的二次开发能力（图查询语言、API/SDK、工具箱等）

【更多阅读，链接：专家观察 | 高并发图数据库系统如何实现？& 图观 | 从电影《满江红》看图数据库的高维力 & 沸点 | 告别“缺芯少魂”：用自研创新的算力之“芯” 夯实金融硬核基础】

[1] 广度优先（Breadth-First-Search，BFS），是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。
[2]点 (Node)，代表真实世界中的实体，即图论中的顶点 (vertex)，在 Ultipa 图系统中也称作节点。
[3] 边 (Edge)，代表真实世界中实体间的关系，即连接两个节点的边。Ultipa 图系统中的边均为有向边。边的两个端点可以相同也可以不相同，相同时边称为自环边（Loop）。
[4]《图数据库原理、架构与应用》; 孙宇熙，嬴图团队；2022-8；机械工业出版社。