目录
题目:
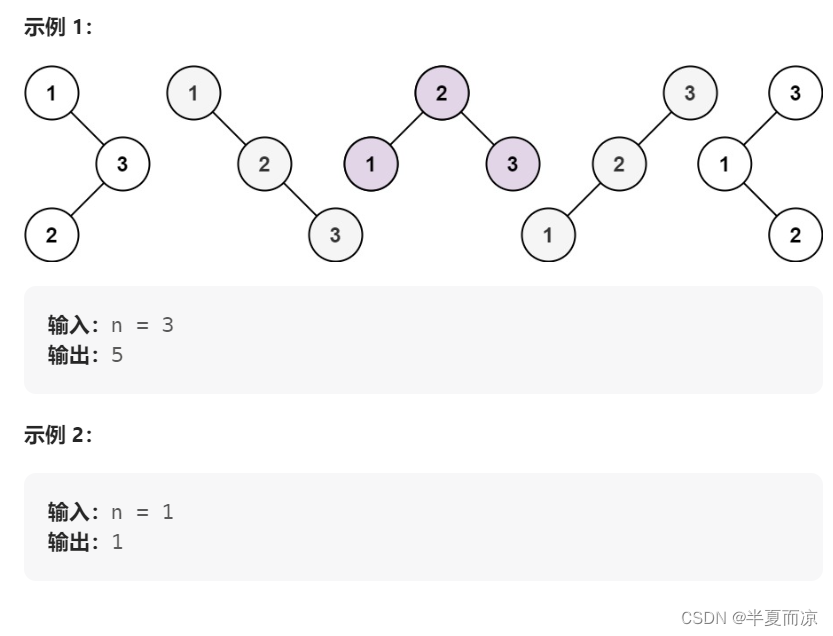
示例:
分析:
代码+运行结果:
题目:
示例:

分析:
接雨水是力扣里非常经典的一道单调栈的题目,使用单调栈的做法就是从左到右将高度依次入栈,保持栈内从栈顶开始升序,在遇到比栈顶更高的高度后,则弹出栈顶元素,并开始按行来计算所积雨水数量,再将后面来的高度入栈。
由于这题很经典,并且讲解的人也不少,因此我就不说单调栈的解法了,我这里介绍一种按列积水的方法。
这里我把示例2做成了图方便看:

我们可以注意到不管是示例一还是示例二,数组的左右两边的列是一定没有积水的,有积水的列都是左边右边都有比自身更高的柱子。
因此我们发现了一个柱子所在的列有没有积水,是根据自身左右边的最高的高度来决定了,因此我们可以用两个数组(一个二维数组也行)来缓存住某索引所在的位置,它的左边最高的高度是多少,以及它的右边最高的高度是多少。
然后这个柱子左右最高的高度中较小的高度减去自身的高度就是本列能积水的最多数量。
我们需要正序遍历一边获取每个柱子左边最高的高度。
再逆序遍历一边获取每个柱子右边最高的高度。
再任意顺序遍历一边将刚刚获取的左右最高高度按照我们刚才说的公式来计算积水数。
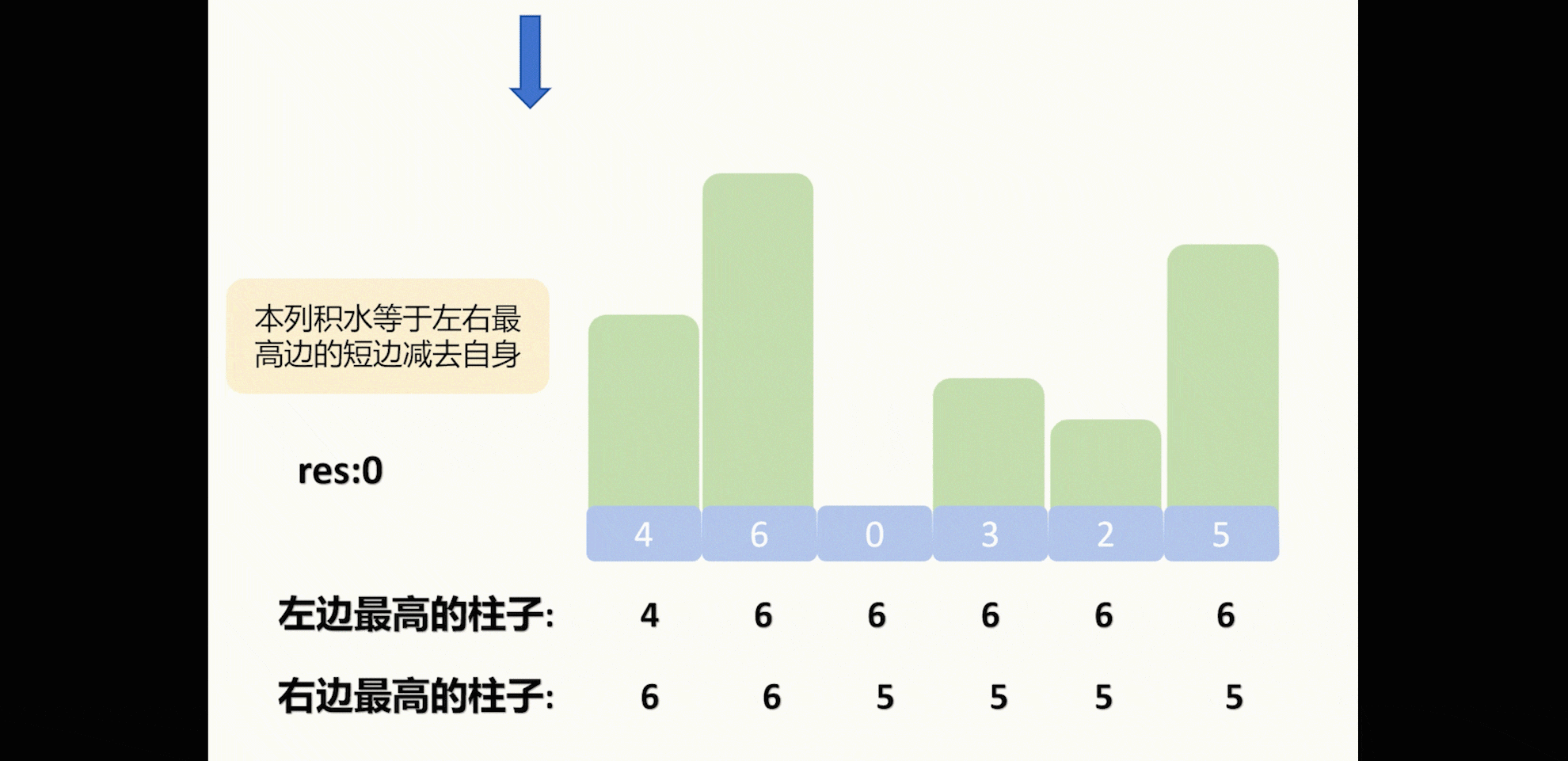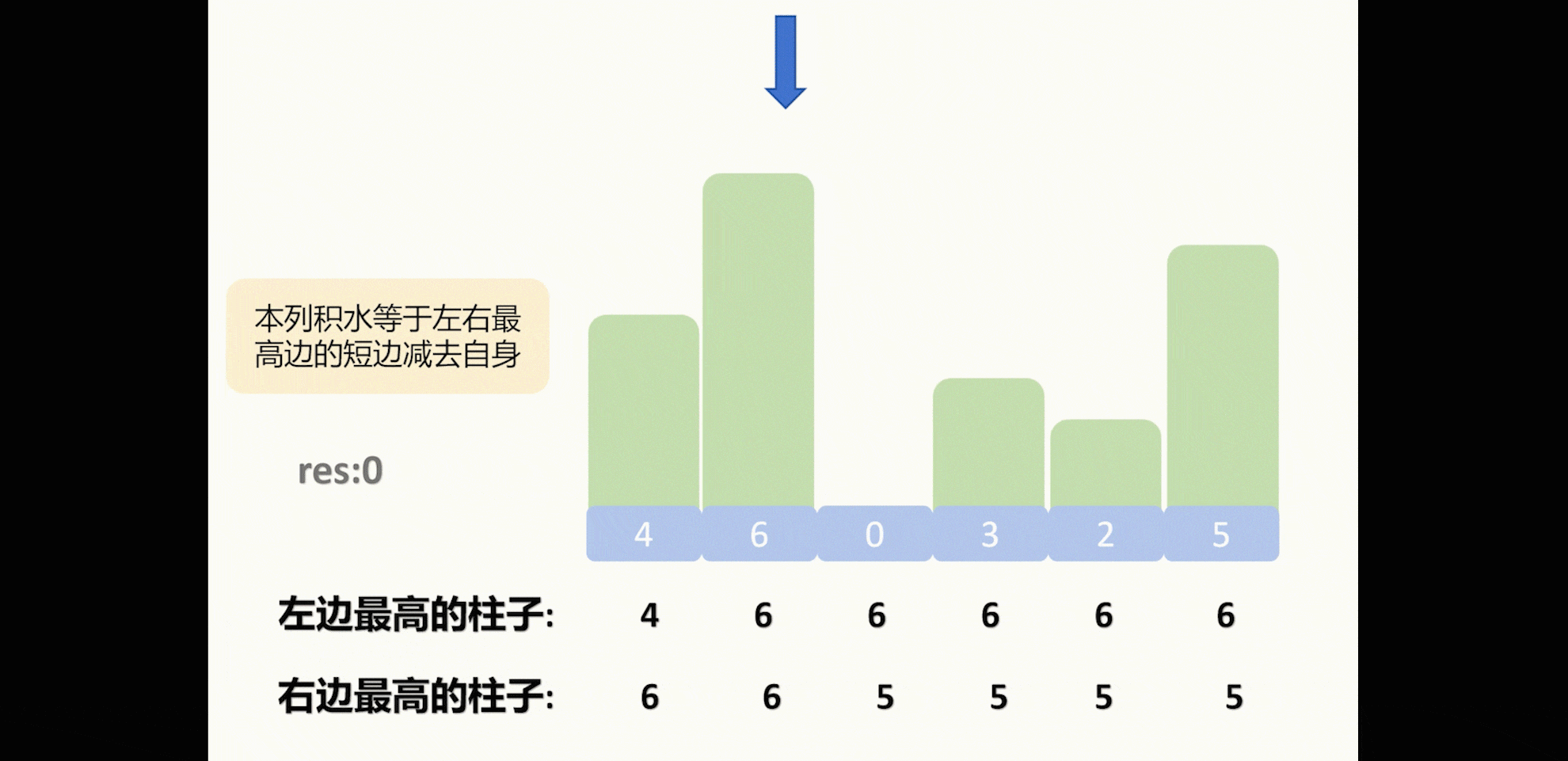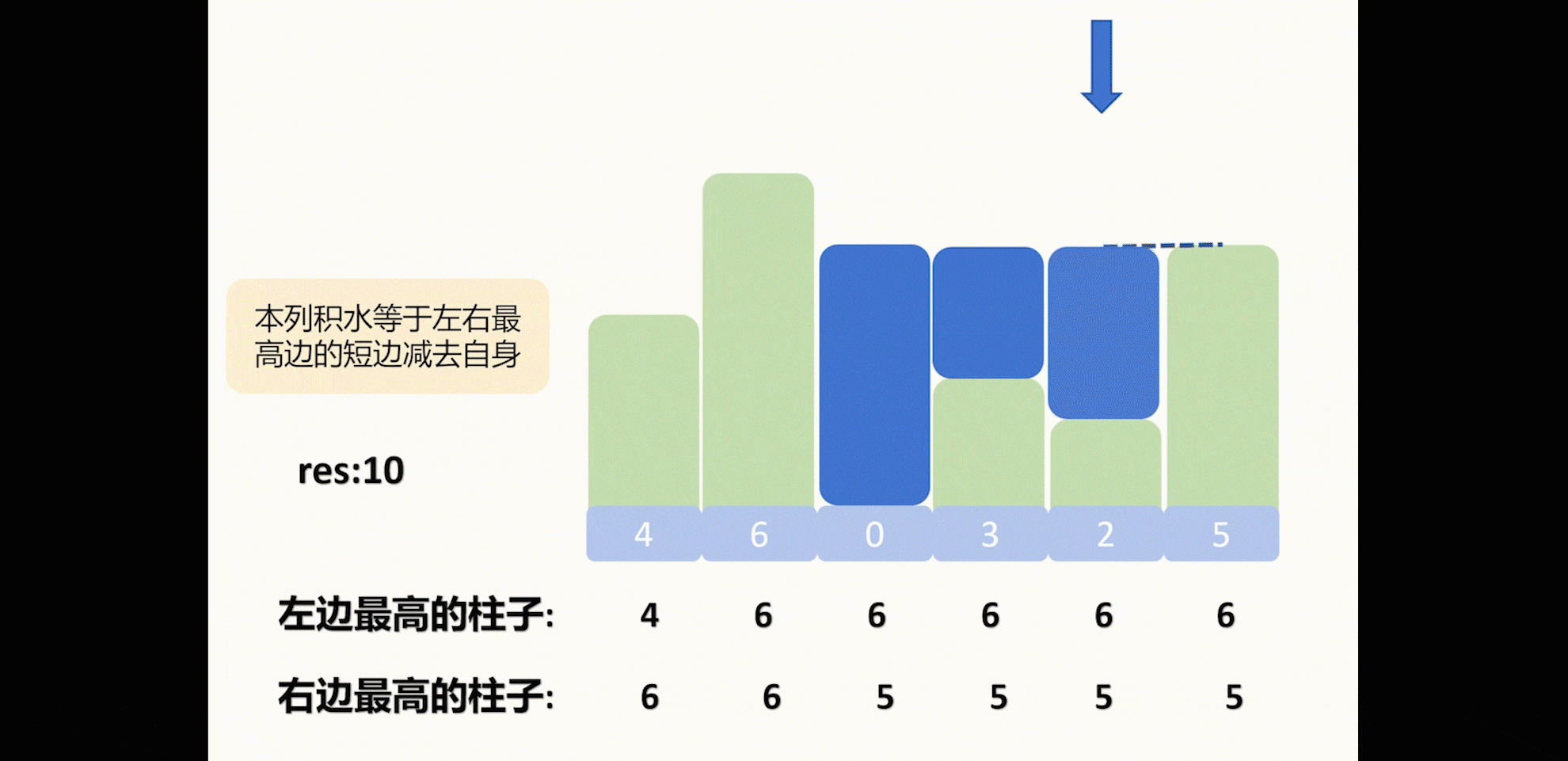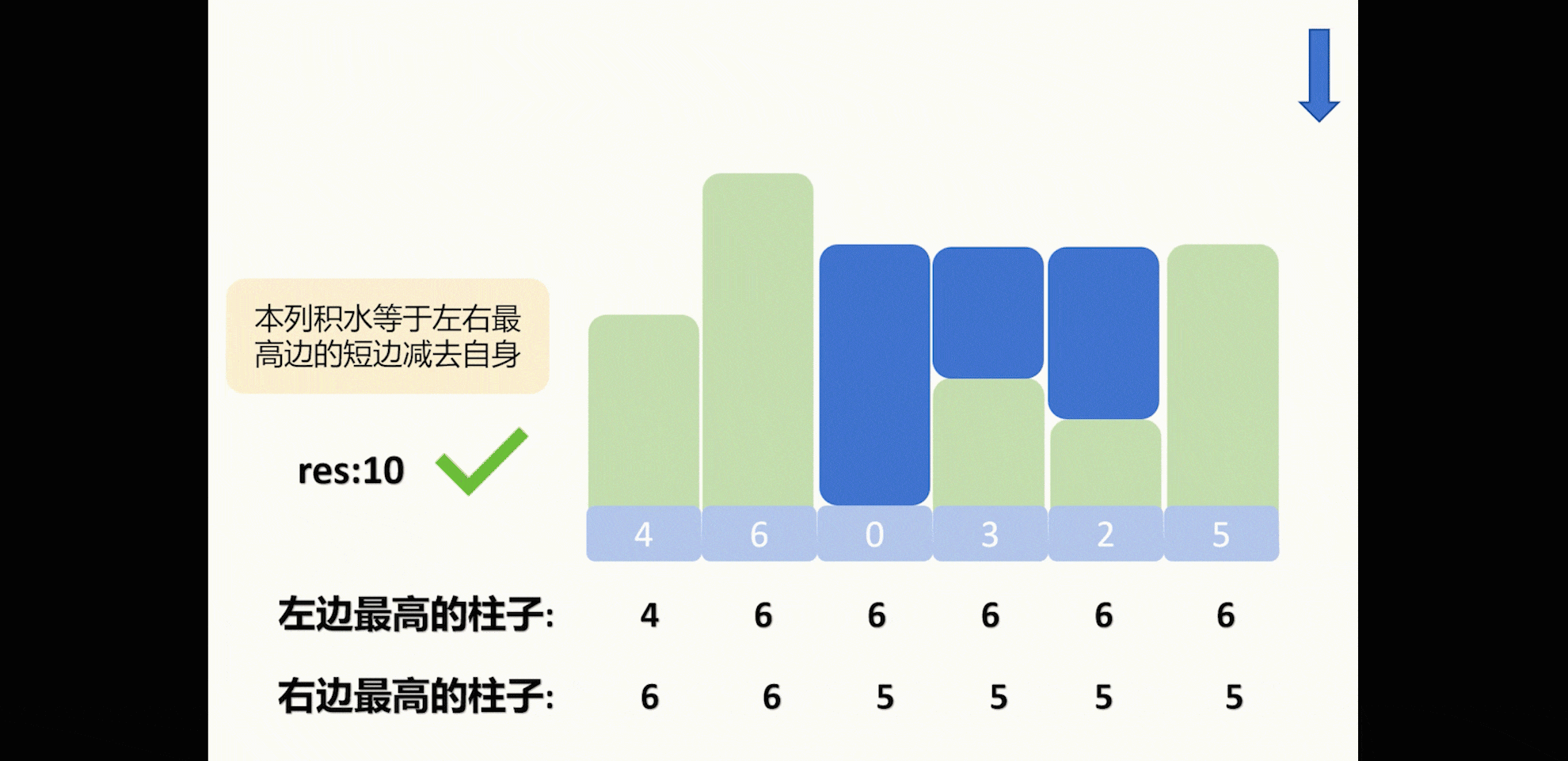
但是这样要遍历三遍,这里有一个更加巧妙的双指针的做法。
我们定义首尾指针分别指向数组的开头和结尾,并且使用左指针来更新左边最高的高度,用右指针来更新右边最高的高度。
哪个指针指向的高度更小,我们就用刚才的公式来计算那一列所积的水,并且移动指针,再更新相应的最高值。
这样左右指针一起遍历一边数组,比最开始遍历3次相比少遍历了2次。
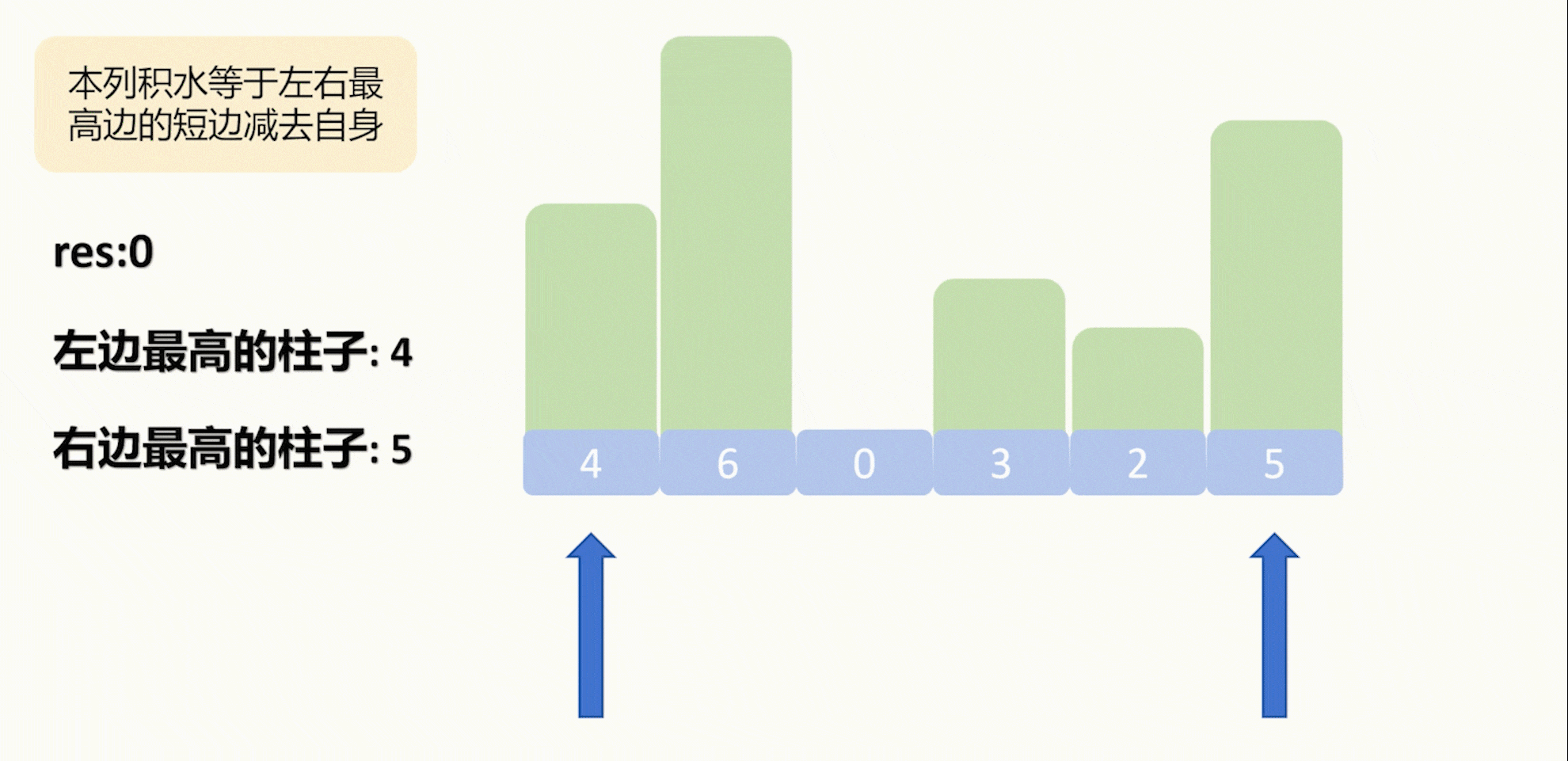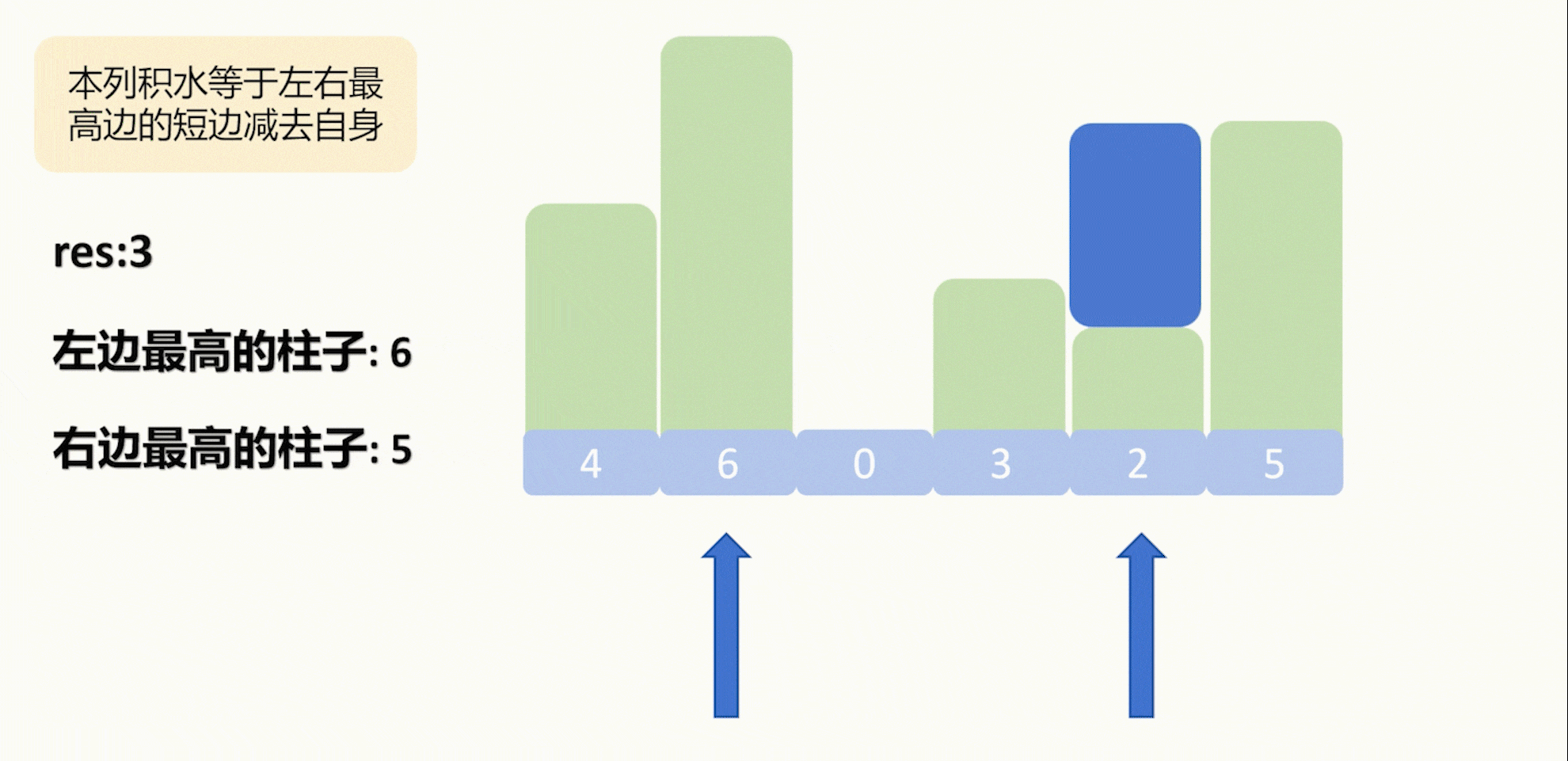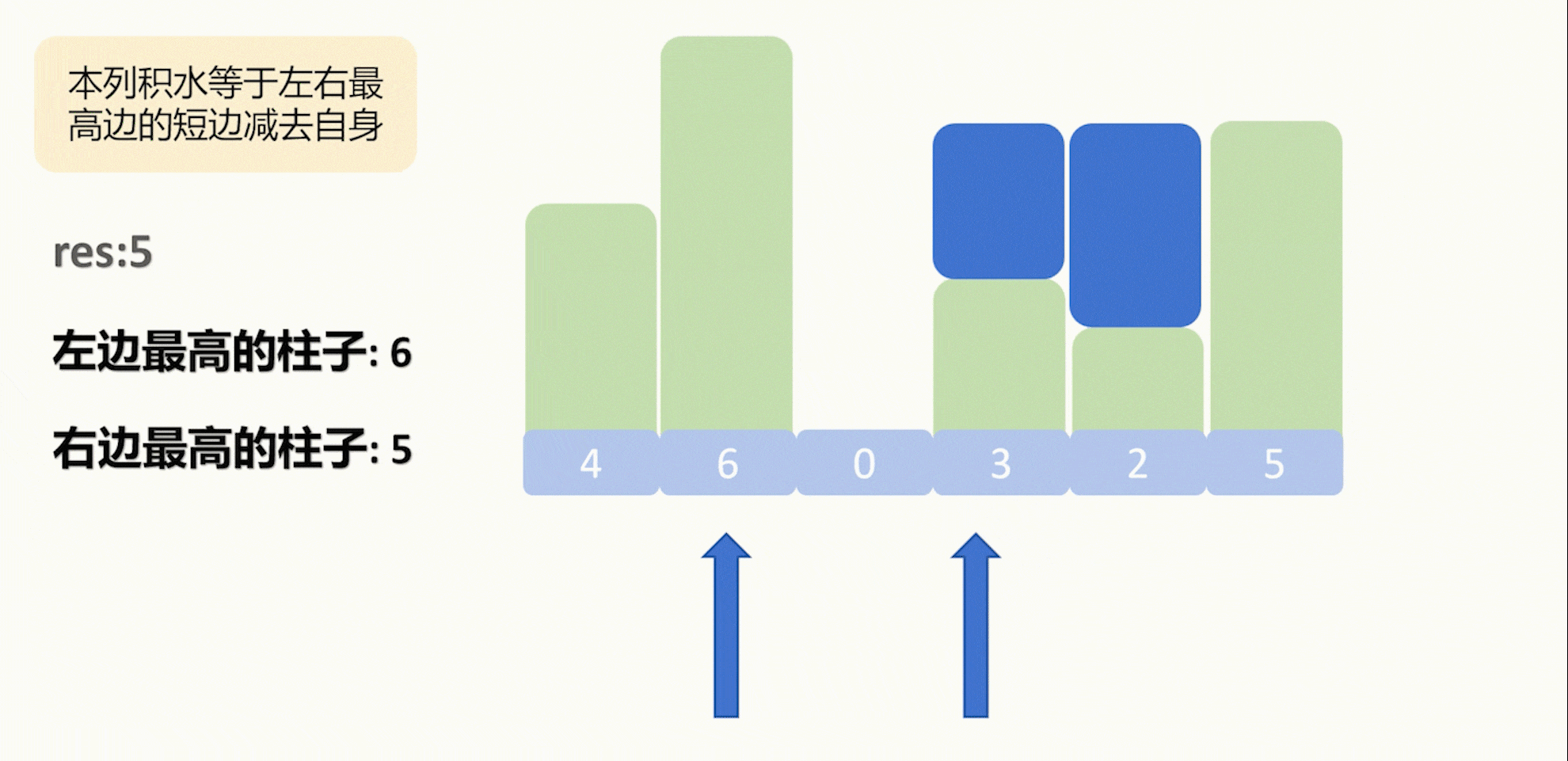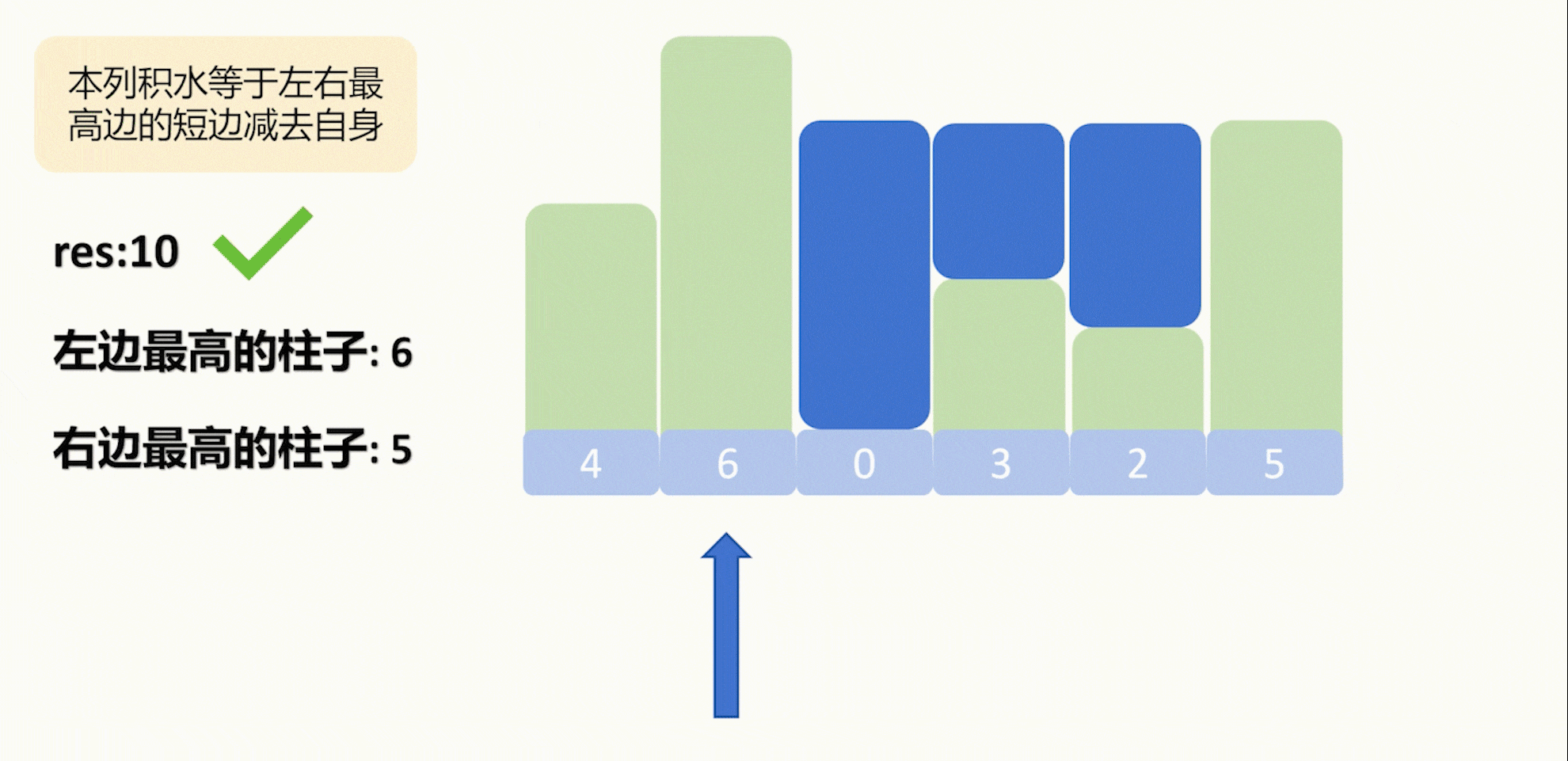
那么大家可能会有疑惑,有没有可能出现这样一种情况,就是我现在要计算一个列的积水,但是这一列的左(右)高度并不是我这一列的左(右)边最大值,像下面这样:

其实大家再从头推导一边就会发现,这样的情况是不会发生的,真实的情况是下面这样:

我们每次计算并移动的都是相对更短的边,因此上面这种少计算积水数的情况是不会发生的。
代码+运行结果:
class Solution {
public:
int trap(vector<int>& height) {
int n=height.size();
//缓存住某索引位置上左边的最高边和右边的最高边
vector<int>lcache(n),rcache(n);
int temp=0;
for(int i=0;i<height.size();++i){
temp=max(temp,height[i]);
lcache[i]=temp;
}
temp=0;
for(int i=n-1;i>=0;--i){
temp=max(temp,height[i]);
rcache[i]=temp;
}
int res=0;
//某索引那一列能储水的部分就是左右两边最矮的一边减去自身高度
for(int i=0;i<n;i++){
res+=min(lcache[i],rcache[i])-height[i];
}
return res;
}
};
class Solution {
public:
int trap(vector<int>& height) {
int l=0,r=height.size()-1;
int maxL=height[l],maxR=height[r];
int res=0;
//双指针
while(l<r){
//更新左右的最高边
maxL=max(maxL,height[l]);
maxR=max(maxR,height[r]);
if(maxR>maxL){
res+=maxL-height[l++];
}else{
res+=maxR-height[r--];
}
}
return res;
}
};