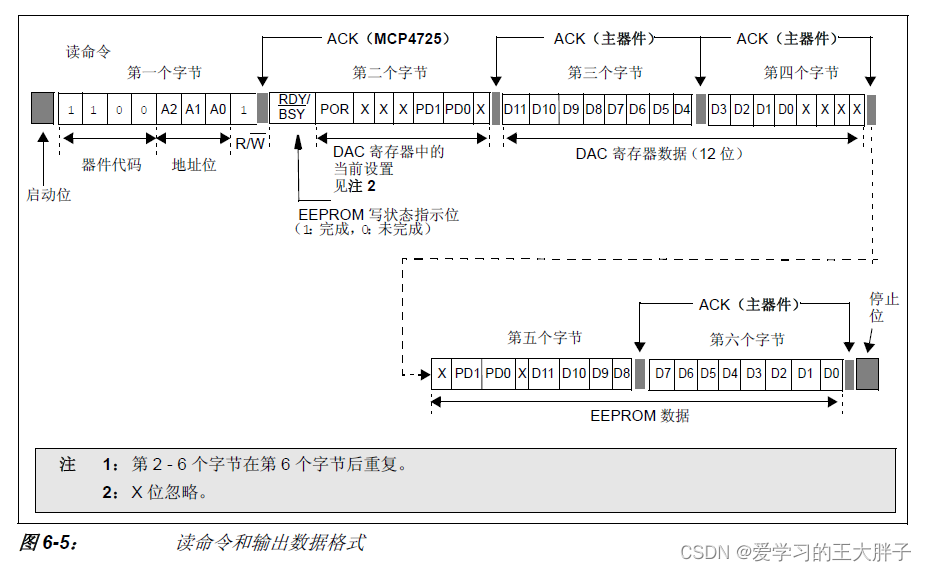
官方解释： 

pcnormals - Estimate normals for point cloud
    This MATLAB function returns a matrix that stores a normal for each
    point in the input ptCloud.

    normals = pcnormals(ptCloud)
    normals = pcnormals(ptCloud,k)

    输入参数
        ptCloud - Object for storing point cloud
            pointCloud object
        k - Number of points used for local plane fitting
            integer greater than or equal to 3

    输出参数
        normals - Normals used to fit a local plane
            M-by-3 | M-by-N-by-3

翻译：

估计点云的法线
这个MATLAB函数返回一个矩阵，该矩阵存储输入ptCloud中每个点的法线。

normal = pcnormals(ptCloud)
normals = pcnormals(ptCloud,k)

输入参数
ptCloud -存储点云的对象
pointCloud对象
k -用于局部平面拟合的点数
大于或等于3的整数

输出参数
法线-用于拟合局部平面的法线
m × 3 | m × n × 3

k是最邻近点的数量，默认是8。

clear
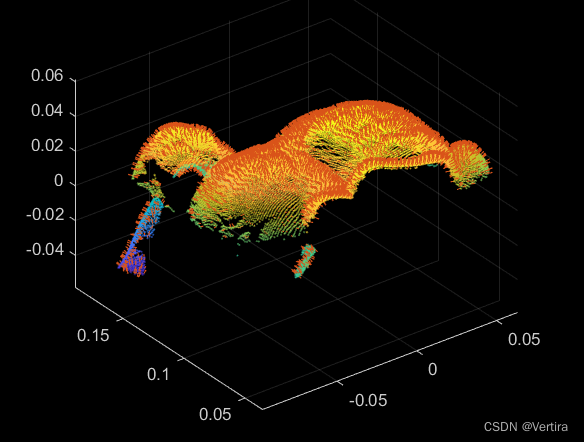
% 加载茶壶的点云
ptCloud = pcread('teapot.ply');
% 计算法向量，6个邻近点
normals = pcnormals(ptCloud);
% 读取x
x = ptCloud.Location(1:5:end,1);
% 读取y
y = ptCloud.Location(1:5:end,2);
% 读取z
z = ptCloud.Location(1:5:end,3);
% uvw为法向量的三列
u = normals(1:5:end,1);
v = normals(1:5:end,2);
w = normals(1:5:end,3);
pcshow(ptCloud)
hold on
% 显示法向量
quiver3(x,y,z,u,v,w);
hold off

 

曲率计算-并计算法向量    直接采用了协方差矩阵进行计算

clear
% 读取茶壶点云
ptCloud = pcread('teapot.ply');
% 读取xyz
a = ptCloud.Location;
%vec储存法向量
vec = zeros(size(a));
%q储存曲率
q = zeros(length(a),1);
 
k = 8;
% 搜索每个点的最邻近点
neighbors = knnsearch(a(:,1:3),a(:,1:3), 'k', k+1);
for i = 1:length(a)
    curtemp = neighbors(i,2:end);
    indpoint = a(curtemp,:);
    % 计算协方差并提取特征
    [v, c] = eig(cov(indpoint));
    %特征值按照升序排列1<2<3
    c = diag(c)';
    %计算特征值的总和
    z = sum(c);
    %计算曲率，用最小特征值除/特征值总和，这也是特征归一化
    p1 = c(:,1)/z;
    q(i,:) = abs(p1);
    %最小特征值对应的列向量就是法向量，dot是交叉相乘
    vec(i,:) = v(:,1)';
end
 
% 读取x
x = ptCloud.Location(1:5:end,1);
% 读取y
y = ptCloud.Location(1:5:end,2);
% 读取z
z = ptCloud.Location(1:5:end,3);
% uvw为法向量的三列
u = vec(1:5:end,1);
v = vec(1:5:end,2);
w = vec(1:5:end,3);
pcshow(ptCloud)
hold on
% 显示法向量
quiver3(x,y,z,u,v,w);
hold off