目录
复习内容:
并集的概念
你能用符号语言和图形语言表示并集这个集合吗?
例1:求并集
例2:求并集
符号解析:
例3:
交集的概念
例4:
例5:
例6:
思考题:
作业:
复习内容:
如何研究两个集合间的基本关系?

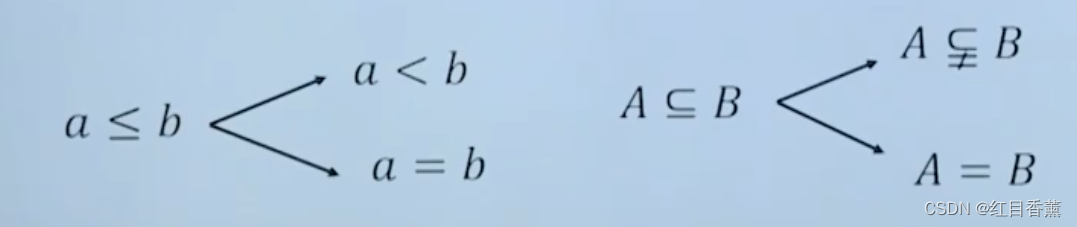
如何判断两集合的关系?
观察集合的特征。
实数有加、减、乘、除等运算,集合是否也有类似的运算呢?
观察下面的集合,你能说出集合C与集合A,B之间的关系吗?
(1) A={1,3,5},B={2,4,6},C= {1,2,3,4,5,6};
(2) A = {x|x是有理数},B = {x|x是无理数},C= {x|x是实数}.
结论:集合C是集合A和集合B中元素合并组成的.
并集的概念
一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与集合B的并集。
记作AUB,读作“A并B”。
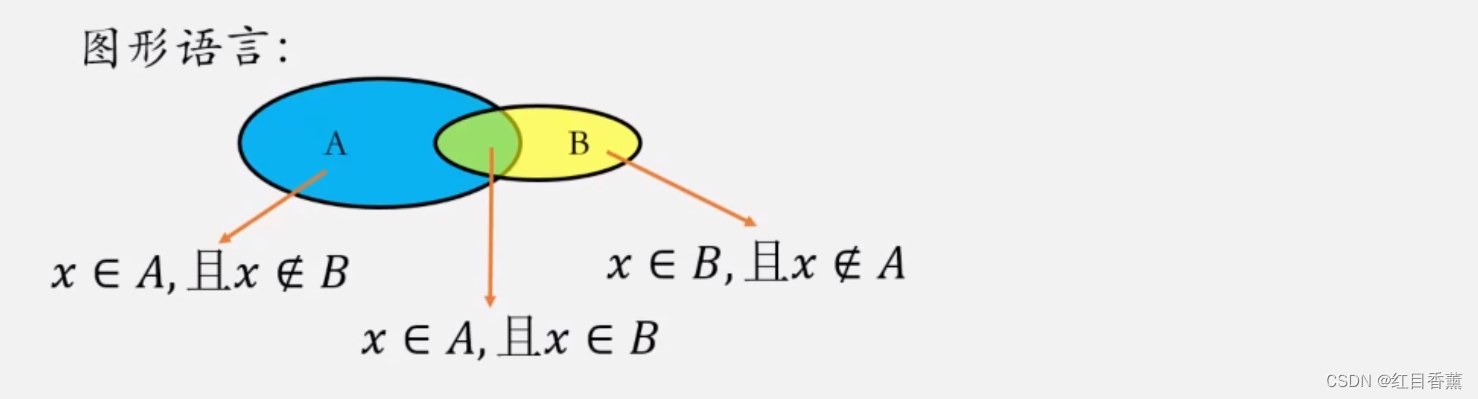
你能用符号语言和图形语言表示并集这个集合吗?
符号语言:AUB = {x| x∈A,或x∈B}
例1:求并集
设A = {4,5,6,8}. B = {3,5,7,8}.求A U B。
答:AUB={3,4,5,6,7,8}

集合的特性:
1、集合具有确定性
2、集合具有互异性
3、集合具有无序性
例2:求并集
设集合A= {x|-1<x ≤ 2},B = {x|1<x ≤ 3},求AUB。

答:AUB={x|-1<x≤3}。
符号解析:
数轴上的点空心是不包含,实心是包含。
例3:
观察下面的集合,集合A,B与集合C之间有什么关系?
(1) A = {2,4,6,8,10},B = {3,5,8,12},C = {8};
(2) A= {x|x是立德中学今年在校的女同学},
B = {x|x是立德中学今年在校的高一年级学生},
C = {x|x是立德中学今年在校的高一年级女同学}。
集合C是所有既属于集合A又属于集合B的元素组成的。
交集的概念
一般地,由所有属于集合A且属于集合B的元素组成的集合,称为集合A与集合B的交集。
记作A∩B,读作'A交B'。
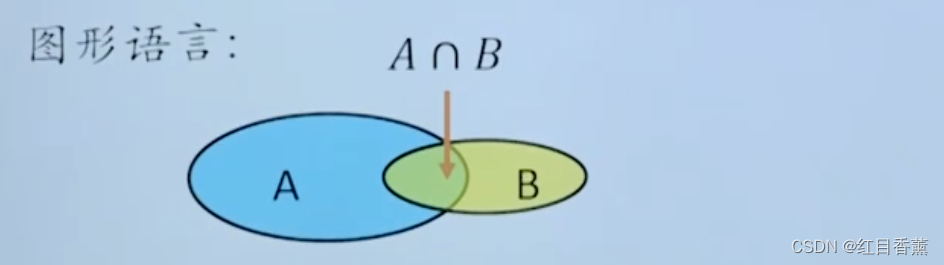
仿照并集的知识,你能用符号语言和图形语言表示交集这个集合吗?
符号语言:A∩B = {x|x∈A,且x∈B}。
例4:
某中学开运动会,设:
A= {x|x是立德中学高一年级参加百米赛跑的同学},
B = {x|x是立德中学高一年级参加跳高比赛的同学},
求A∩B。
答:A∩B = {x|x是立德中学高一年级既参加百米赛跑又参加跳高比赛的同学}.
例5:
例4设平面内直线l1上的点的集合为L1,直线l2上点的集合为L2,试用集合的运算表示l,l2的位置关系.
解:
(1) 直线l,l2相交于点P,可表示为L1∩L2 ={点P};
(2) 直线l1,l2平行,可表示为L1∩L2 = ∅;
(3) 直线l1,l2重合,可表示为L1∩L2=L1=L2。
例6:
A = {x|x是等腰三角形},B = {x|x是直角三角形},求A ∩ B,A U B。
解:
A∩B = {x|x是等腰直角三角形};
A∪B = {x|x是等腰或直角三角形}。
思考题:
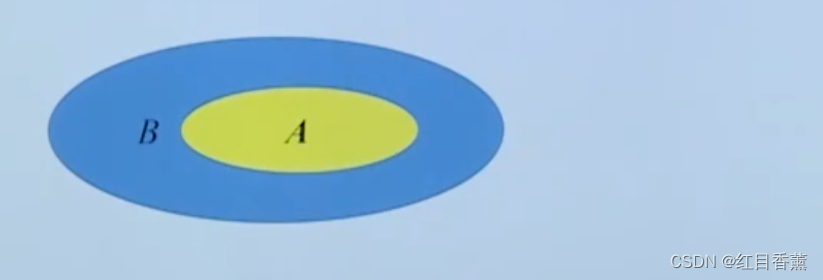
若AB,则A ∩ B = A,AUB = B。

作业:
1、如何理解并集和交集?它们之间有什么联系与区别?
解:
(1)通过集合的交、并运算,可以得到与原集合紧密关联的交集,并集;
(2)交集、并集是一个集合,要关注集合元素的特征;
(3)并集由所有属于集合A或属于集合B的元素组成;交集由所有既属于集合A又属于集合B的元素组成。
2、如何求两个集合的并集和交集?
解:
(1)在求集合的交集并集时,为增强直观性,应数形结合的研究问题;
(2) 求连续数集的交集并集时可运用数轴来表示;
(3)在研究元素个数比较少的集合或研究抽象集合关系时,可运用韦恩图来表示。