自从Sims（1980）发表开创性的论文以来，向量自回归模型已经成为宏观经济研究中的关键工具。最近我们被客户要求撰写关于向量自回归（VAR）的研究报告，包括一些图形和统计输出。这篇文章介绍了VAR分析的基本概念，并指导了简单模型的估算过程。 

单变量自回归

VAR代表向量自回归。为了理解这意味着什么，让我们首先来看一个简单的单变量（即仅一个因变量或内生变量）自回归（AR）模型，其形式为yt=a1yt−1+et。 

视频：向量自回归VAR数学原理及R软件经济数据脉冲响应分析实例

，时长12:01

平稳性

在估算此类模型之前，应始终检查所分析的时间序列是否稳定，即它们的均值和方差随时间变化是恒定的，并且不显示任何趋势行为。 

有一系列统计检验，例如Dickey-Fuller，KPSS或Phillips-Perron检验，以检验序列是否稳定。另一种非常常见的做法是绘制序列并检查其是否围绕恒定的平均值（即水平线）移动。如果是这种情况，它很可能是稳定的。 

自回归滞后模型

像AR（p）模型一样，仅凭其自身的滞后对宏观经济变量进行回归可能是一种限制性很大的方法。通常，更合适的假设是还有其他因素。通过包含因变量的滞后值以及其他（即，外生）变量的同期和滞后值的模型来实现这种想法。同样，这些外生变量应该是稳定的。对于内生变量yt和外生变量xt例如自回归分布滞后或ADL，模型可以写成

yt=a1yt−1+b0xt+b1xt−1+et.

这种ADL模型的预测性能可能会比简单的AR模型更好。但是，如果外生变量也依赖于内生变量的滞后值怎么办？这意味着xt也是内生的，还有进一步的空间可以改善我们的预测。

向量自回归模型

 因此，如上所述，VAR模型可以重写为一系列单独的ADL模型。实际上，可以通过分别估计每个方程来估计VAR模型。

标准VAR模型的协方差矩阵是对称的，即，对角线右上角的元素（“上三角”）将对角线左下角的元素（“下三角”）镜像。这反映了这样一种想法，即内生变量之间的关系仅反映相关性，并且不允许做出因果关系的陈述，因为在每个方向上的影响都是相同的。 

在所谓的结构化 VAR（SVAR）模型的背景下分析了同时因果关系，或更确切地说，是变量之间的结构关系，该模型对协方差矩阵施加了限制 。 

在本文中，我考虑VAR（2）过程。 

此示例的人工样本是在R中生成的

set.seed(123) # 由于可复制性的考虑，重置随机数发生器

# 生成样本
t <- 200 # 时间序列观察数
k <- 2 # 内生变量数
p <- 2 # 滞后阶数

# 生成系数矩阵
A.1 <- matrix(c(-.3, .6, -.4, .5), k) # 滞后系数矩阵1
A.2 <- matrix(c(-.1, -.2, .1, .05), k) # 滞后系数2
A <- cbind(A.1, A.2) # 系数矩阵

# 生成序列

series <- matrix(0, k, t + 2*p) # 带有0的原始序列
for (i in (p + 1):(t + 2*p)){ # 生成e ~ N(0,0.5)的序列
  series[, i] <- A.1%*%series[, i-1] + A.2%*%series[, i-2] + rnorm(k, 0, .5)
}

series <- ts(t(series[, -(1:p)])) # 转换为时间序列格式
names <- c("V1", "V2") # 重命名变量

plot.ts(series) # 绘制序列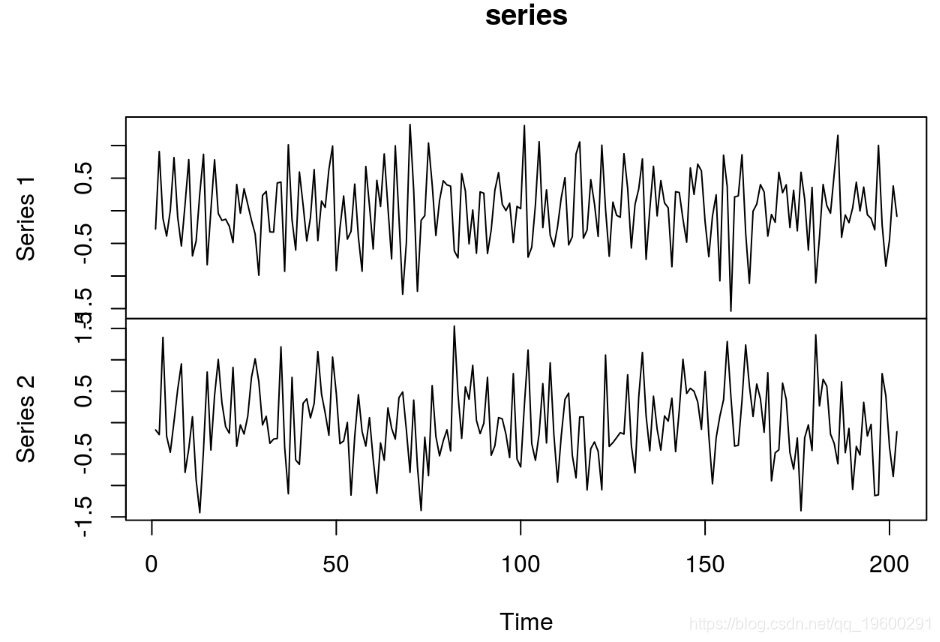

估算值

简单VAR模型的参数和协方差矩阵的估计很简单。

为了估计VAR模型，加载并指定数据（y）和 模型。 

 比较

VAR分析中的一个中心问题是找到滞后的阶数，以产生最佳结果。模型比较通常基于信息标准，例如AIC，BIC或HQ。通常，由于是小样本预测，AIC优于其他标准。但是，BIC和HQ在大型样本中效果很好 。

可以计算标准信息标准以找到最佳模型。在此示例中，我们使用AIC：

 通过查看，summary我们可以看到AIC建议使用2的阶数。

summary(var.aic)

## 
## VAR Estimation Results:
## ========================= 
## Endogenous variables: Series.1, Series.2 
## Deterministic variables: none 
## Sample size: 200 
## Log Likelihood: -266.065 
## Roots of the characteristic polynomial:
## 0.6611 0.6611 0.4473 0.03778
## Call:
## VAR(y = series, type = "none", lag.max = 5, ic = "AIC")
## 
## 
## Estimation results for equation Series.1: 
## ========================================= 
## Series.1 = Series.1.l1 + Series.2.l1 + Series.1.l2 + Series.2.l2 
## 
##             Estimate Std. Error t value Pr(>|t|)    
## Series.1.l1 -0.19750    0.06894  -2.865  0.00463 ** 
## Series.2.l1 -0.32015    0.06601  -4.850 2.51e-06 ***
## Series.1.l2 -0.23210    0.07586  -3.060  0.00252 ** 
## Series.2.l2  0.04687    0.06478   0.724  0.47018    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## Residual standard error: 0.4638 on 196 degrees of freedom
## Multiple R-Squared: 0.2791,  Adjusted R-squared: 0.2644 
## F-statistic: 18.97 on 4 and 196 DF,  p-value: 3.351e-13 
## 
## 
## Estimation results for equation Series.2: 
## ========================================= 
## Series.2 = Series.1.l1 + Series.2.l1 + Series.1.l2 + Series.2.l2 
## 
##             Estimate Std. Error t value Pr(>|t|)    
## Series.1.l1  0.67381    0.07314   9.213  < 2e-16 ***
## Series.2.l1  0.34136    0.07004   4.874 2.25e-06 ***
## Series.1.l2 -0.18430    0.08048  -2.290   0.0231 *  
## Series.2.l2  0.06903    0.06873   1.004   0.3164    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## Residual standard error: 0.4921 on 196 degrees of freedom
## Multiple R-Squared: 0.3574,  Adjusted R-squared: 0.3443 
## F-statistic: 27.26 on 4 and 196 DF,  p-value: < 2.2e-16 
## 
## 
## 
## Covariance matrix of residuals:
##          Series.1 Series.2
## Series.1  0.21417 -0.03116
## Series.2 -0.03116  0.24154
## 
## Correlation matrix of residuals:
##          Series.1 Series.2
## Series.1    1.000   -0.137
## Series.2   -0.137    1.000

仔细观察结果，我们可以将真实值 与模型的参数估计值进行比较：

# 真实值
A
##      [,1] [,2] [,3] [,4]
## [1,] -0.3 -0.4 -0.1 0.10
## [2,]  0.6  0.5 -0.2 0.05
# Extract coefficients, standard errors etc. from the object
# produced by the VAR function
est_coefs <- coef(var.aic)

# 仅提取两个因变量的系数，并将它们组合为一个矩阵

# 输出四舍五入的估计值
round(est_coefs, 2)
##      Series.1.l1 Series.2.l1 Series.1.l2 Series.2.l2
## [1,]       -0.20       -0.32       -0.23        0.05
## [2,]        0.67        0.34       -0.18        0.07

所有估计值都有正确的符号，并且相对接近其真实值。 

脉冲响应

一旦我们确定了最终的VAR模型，就必须解释其估计的参数值。由于VAR模型中的所有变量都相互依赖，因此单个参数值仅提供 有限信息。为了更好地了解模型的动态行为，使用了脉冲响应（IR）。可以绘制响应变量的轨迹，产生在许多宏观论文中都可以找到的那些波浪曲线。

在下面的示例中，我们想知道受到冲击后序列2的行为。指定了我们想要脉冲响应的模型和变量后，我们将时间范围设置n.ahead为20。该图给出了序列2的响应。 

# 计算脉冲响应

# 绘制脉冲响应
plot(ir.1)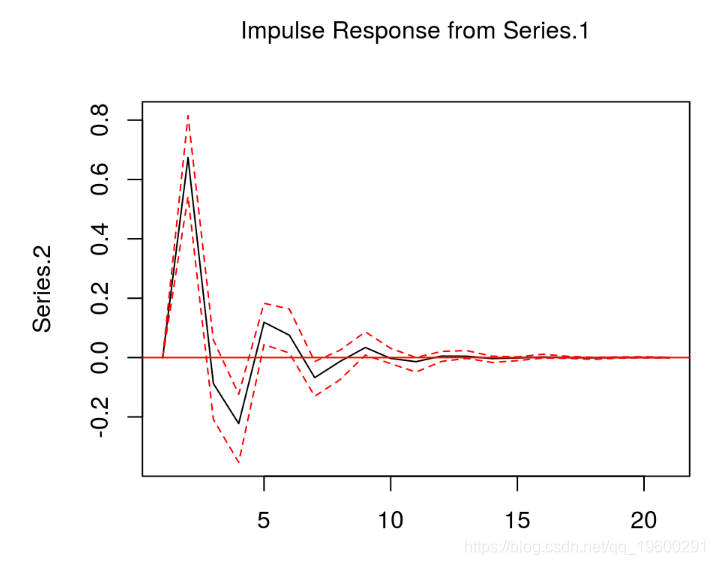

请注意，正交选项很重要，因为它说明了变量之间的关系。在我们的示例中，我们已经知道不存在这样的关系，因为真正的方差-协方差矩阵（或简称协方差矩阵）在非对角元素中是对角为零的对角线。但是，由于具有200个观测值的有限时间序列数据限制了参数估计的精度，因此协方差矩阵的非对角元素具有正值，这意味着 非零同时效应。为了在IR中排除这种情况，我们设置了ortho = FALSE。结果是，脉冲响应在周期0中从零开始。 也可以尝试另一种方法并进行设置ortho = TRUE，那么绘图从零开始。 

 要了解这一点，还可以计算并绘制累积脉冲响应函数，以了解 总体长期影响：

# 计算脉冲响应

# 绘图
plot(ir.2)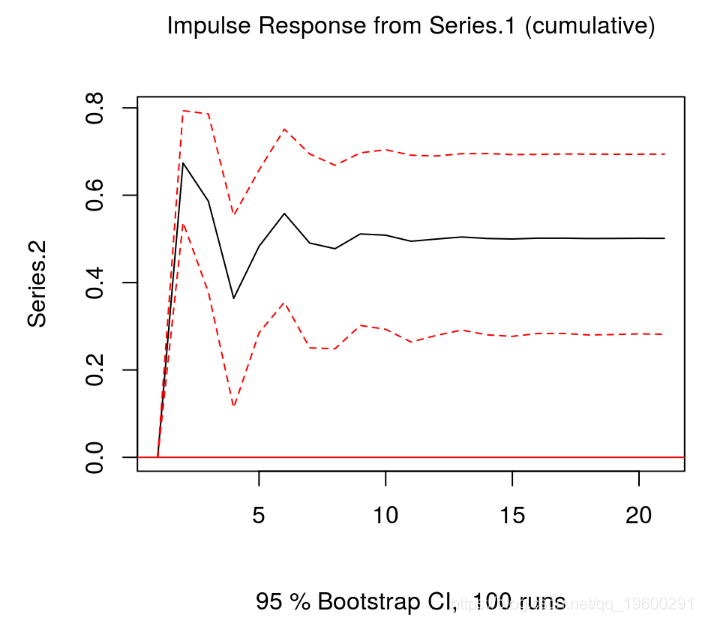

我们看到，尽管序列2对序列1中的 反应在某些时期是负面的，但总体效果却是显着正面。

---