In mathematics, an existence theorem is a theorem which asserts the existence of a certain object.[1] It might be a statement which begins with the phrase “there exist(s)”, or it might be a universal statement whose last quantifier is existential (e.g., “for all x, y, … there exist(s) …”). In the formal terms of symbolic logic, an existence theorem is a theorem with a prenex normal form involving the existential quantifier, even though in practice, such theorems are usually stated in standard mathematical language. For example, the statement that the sine function is continuous everywhere, or any theorem written in big O notation, can be considered as theorems which are existential by nature—since the quantification can be found in the definitions of the concepts used.

A controversy that goes back to the early twentieth century concerns the issue of purely theoretic existence theorems, that is, theorems which depend on non-constructive foundational material such as the axiom of infinity, the axiom of choice or the law of excluded middle. Such theorems provide no indication as to how to construct (or exhibit) the object whose existence is being claimed. From a constructivist viewpoint, such approaches are not viable as it lends to mathematics losing its concrete applicability,[2] while the opposing viewpoint is that abstract methods are far-reaching,[further explanation needed] in a way that numerical analysis cannot be.

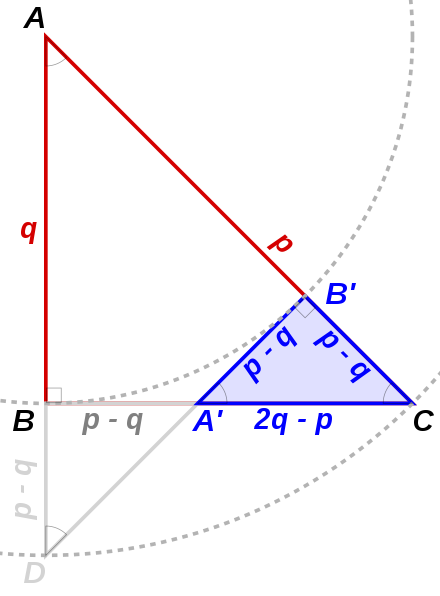
Geometrical proof that an irrational number exists: If the isosceles right triangle ABC had integer side lengths, so had the strictly smaller triangle A’B’C. Repeating this construction would obtain an infinitely descending sequence of integer side lengths.

1 ‘Pure’ existence results

In mathematics, an existence theorem is purely theoretical if the proof given for it does not indicate a construction of the object whose existence is asserted. Such a proof is non-constructive,[3] since the whole approach may not lend itself to construction.[4] In terms of algorithms, purely theoretical existence theorems bypass all algorithms for finding what is asserted to exist. These are to be contrasted with the so-called “constructive” existence theorems,[5] which many constructivist mathematicians working in extended logics (such as intuitionistic logic) believe to be intrinsically stronger than their non-constructive counterparts.

Despite that, the purely theoretical existence results are nevertheless ubiquitous in contemporary mathematics. For example, John Nash’s original proof of the existence of a Nash equilibrium in 1951 was such an existence theorem. An approach which is constructive was also later found in 1962.[6]

2 Constructivist ideas

From the other direction, there has been considerable clarification of what constructive mathematics is—without the emergence of a ‘master theory’. For example, according to Errett Bishop’s definitions, the continuity of a function such as sin(x) should be proved as a constructive bound on the modulus of continuity, meaning that the existential content of the assertion of continuity is a promise that can always be kept. Accordingly, Bishop rejects the standard idea of pointwise continuity, and proposed that continuity should be defined in terms of “local uniform continuity”.[7] One could get another explanation of existence theorem from type theory, in which a proof of an existential statement can come only from a term (which one can see as the computational content).

3 See also

Constructive proof
Constructivism (philosophy of mathematics)
Uniqueness theorem