目录
递归函数介绍
递归函数的作用
案例:实现10以内阶乘
递归思想
递归的编写
斐波那契数列(实战)
循环实现
递归实现
递归函数介绍
递归函数是指在函数的定义中调用函数本身的过程。递归函数可以用于解决那些可以通过将大问题拆分为更小的相似子问题来解决的情况。它通常包含两个关键部分:基本情况(递归终止条件)和递归调用。
基本情况(递归终止条件)是一个条件判断,当满足该条件时,递归函数不再调用自身,而是返回一个特定的值或执行特定的操作。这个基本情况用于避免递归无限进行,导致栈溢出错误。
递归调用是指在函数的定义中使用相同的函数来解决规模更小的子问题。通过不断地调用自身,并且每次调用时传递一个规模更小的子问题,递归函数最终会达到基本情况,从而逐步解决原始问题。
递归函数的设计需要满足以下要求:
-
定义明确的基本情况,确保递归函数可以终止。
-
在每次递归调用中,问题的规模都应该比原始问题减小,以便最终达到基本情况。
-
确保递归函数的每次调用都在不同的数据上进行操作,避免重复计算。
递归函数在解决许多问题时非常有用,如计算阶乘、斐波那契数列、二叉树遍历、图搜索等。它们可以提供一种简洁和直观的解决方案,并且在某些情况下比迭代方式更加简单和有效。
注意
使用递归容易产生栈溢出的错误
- 递归一定要有出口,否则就是"死循环"的递归
- 递归的次数不能太多
递归函数的作用
-
解决复杂问题:递归函数能够将一个复杂的问题分解为更小、更简单的子问题,从而使问题的解决变得更加直观和简单。
-
提高代码可读性:递归函数能够以一种自然而直观的方式描述问题的解决过程,使代码更易于理解和维护。
-
优化算法实现:某些问题的最优解往往可以通过递归函数来实现,例如分治算法、回溯算法等。递归函数可以帮助我们以更简洁的方式实现这些算法,提高代码的效率和可扩展性。
-
处理树形结构和递归数据结构:递归函数常用于处理树形结构、图等递归数据结构。例如,在树的遍历、搜索和构建等问题中,递归函数能够很好地表达和处理这些结构。
-
函数式编程:递归是函数式编程的重要概念之一,函数式编程强调使用函数来进行问题求解。递归函数是函数式编程中常用的工具,能够实现函数的组合和高阶函数的应用。
案例:实现10以内阶乘
def jie_cheng1(num:int) ->int:
count = 1
for i in range(1,num+1):
count *=i
return count
print(jie_cheng1(10))
递归思想
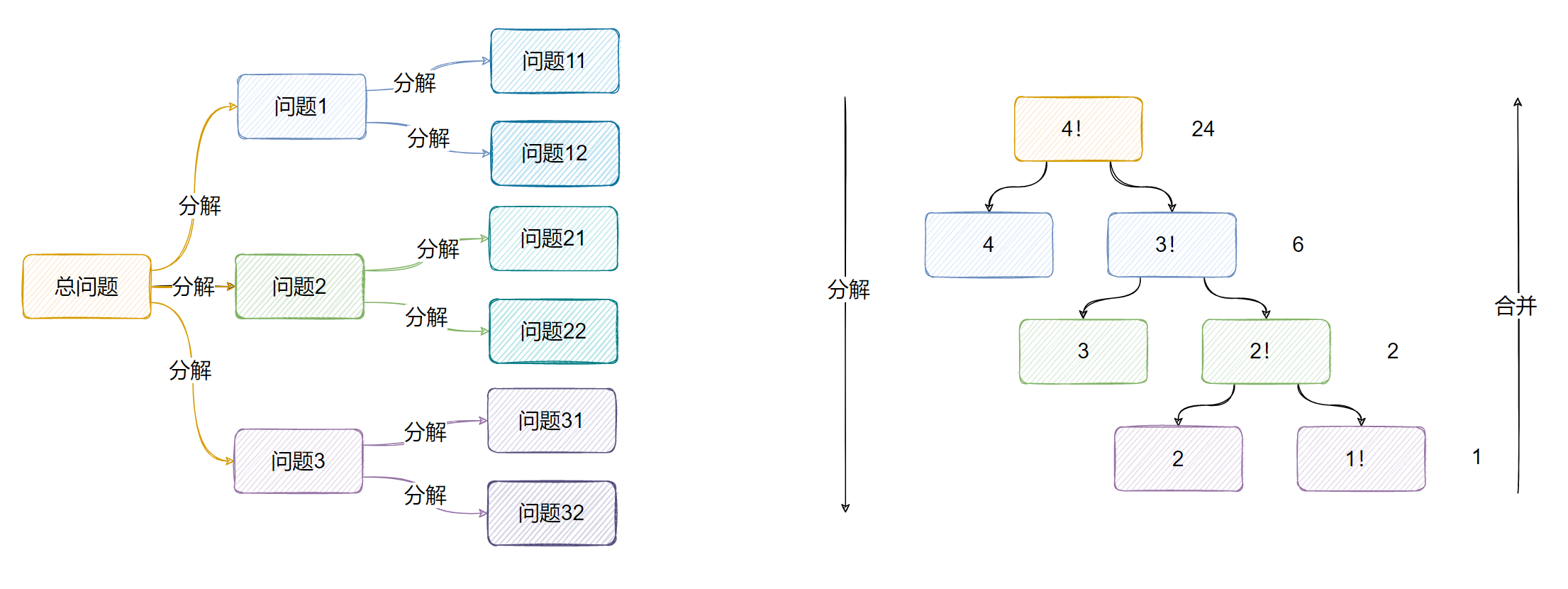
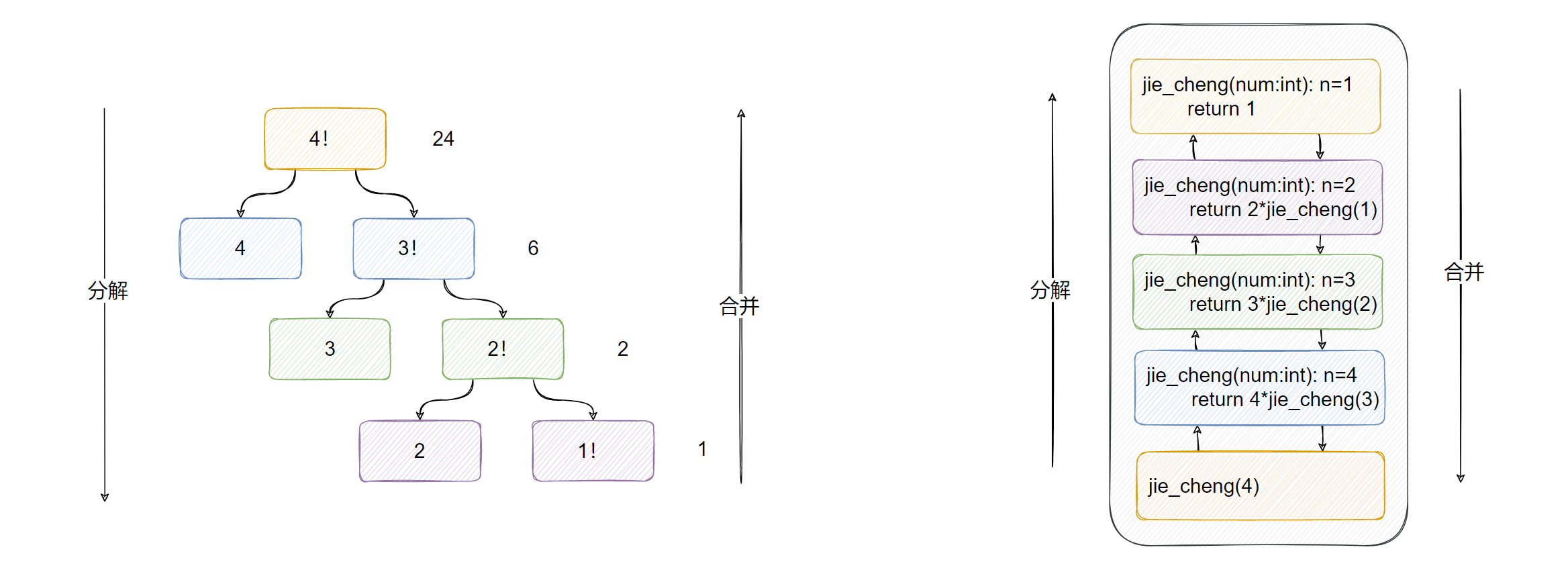
递归其主要思想在于:
- 将问题分为规模更小的相同问题,持续分解,直到问题规模小到可以用非常简单直接的方式来解决
- 分解完后,再合并结果
递归的编写
- 定义 一个函数
- 找到出口条件
- 找到规律
def jie_cheng2(num:int):
if num == 1:
return 1
else:
return num * jie_cheng2(num-1)
print(jie_cheng2(10))
斐波那契数列(实战)
问题
有一对兔子,从出生第三个月起每个月都生一对兔子,小兔子长到第三个月后,每个月又生一只兔子,假如兔子都不死,问第二十个月的兔子对数为多少
斐波那契数列,又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”
斐波那契数列指的是这样一个数列:1,1,2,3,5,8,13,21,34,55,89...
这个数列从第3项开始,每一项都等于前两项之和
循环实现
def fib1(n:int) -> int:
if n <= 0:
return 0
elif n == 1 or n == 2:
return 1
a = b = 1
rs = 2
# 1 1 2 3
for i in range(3,n):
a = b
b = rs
rs = a + b
return rs
递归实现
def fib2(n:int) -> int:
if n <= 0:
return 0
elif n == 1 or n == 2:
return 1
else:
return fib2(n-1) + fib2(n-2)