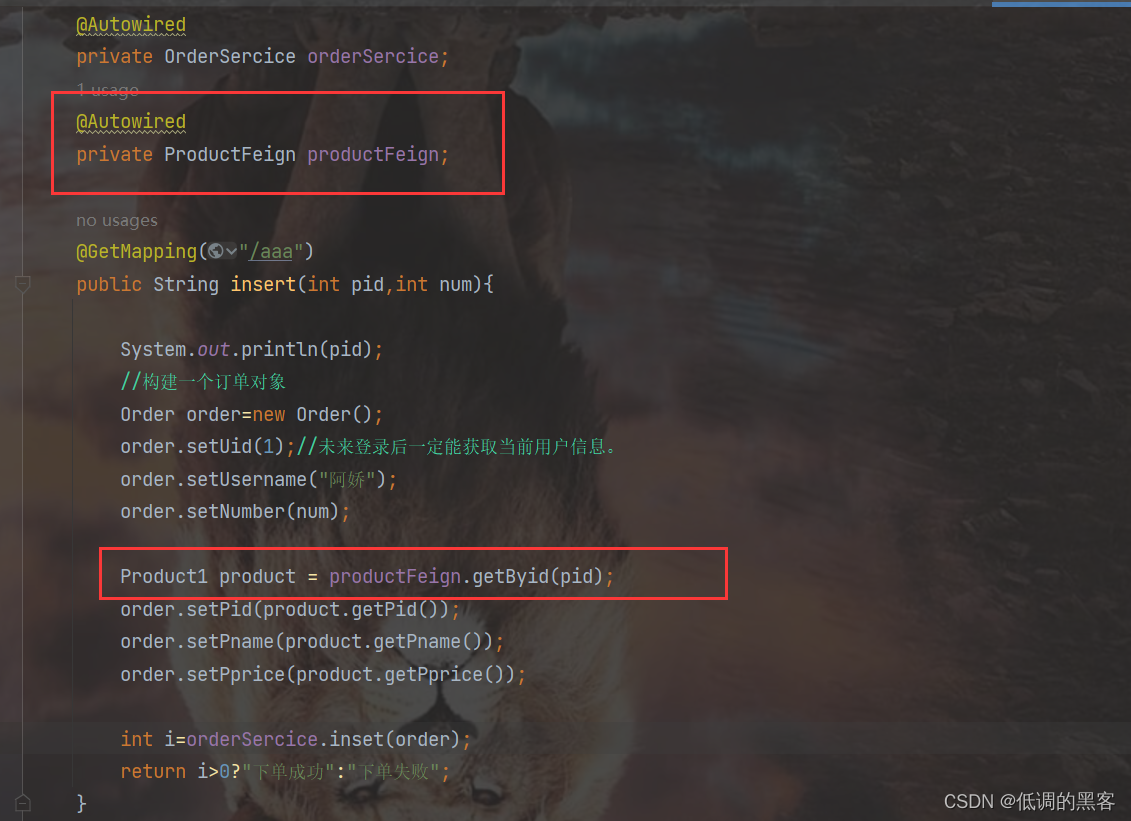
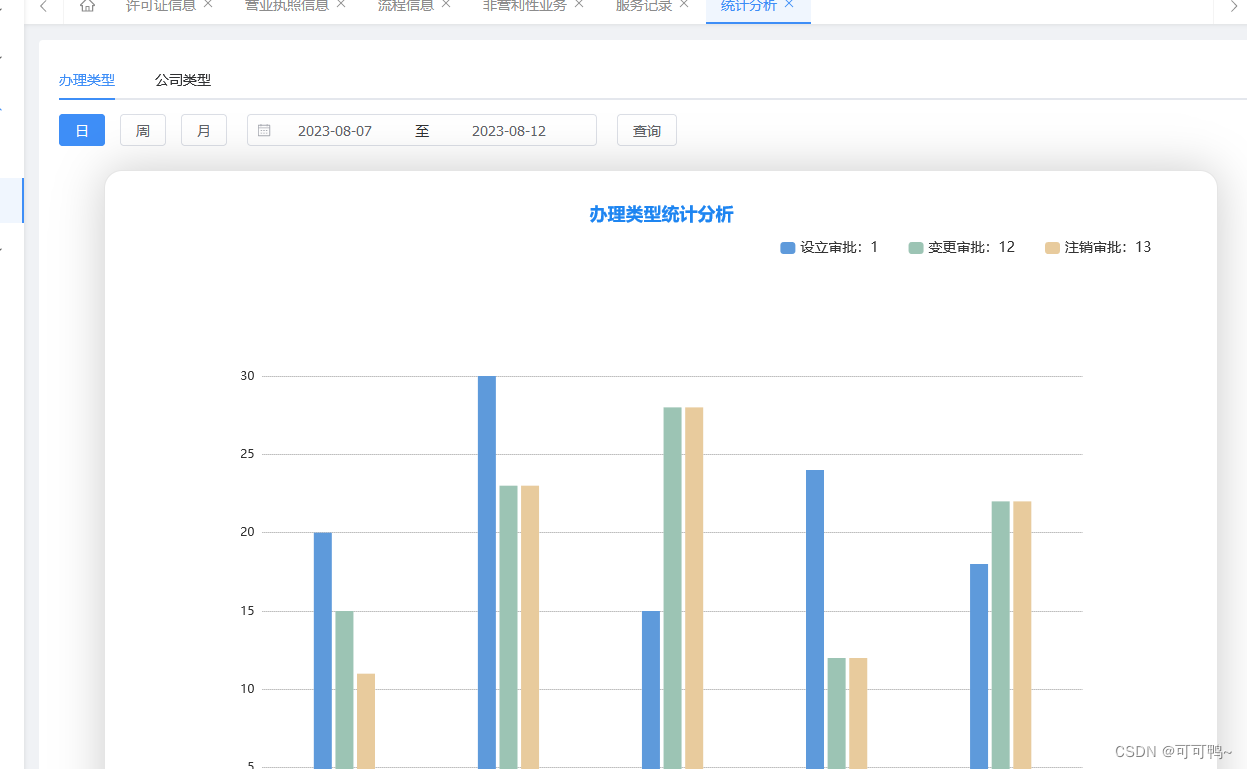
在vue2中,要实现一些方法(增删改查)一般都是写在一起的。如下图所示:
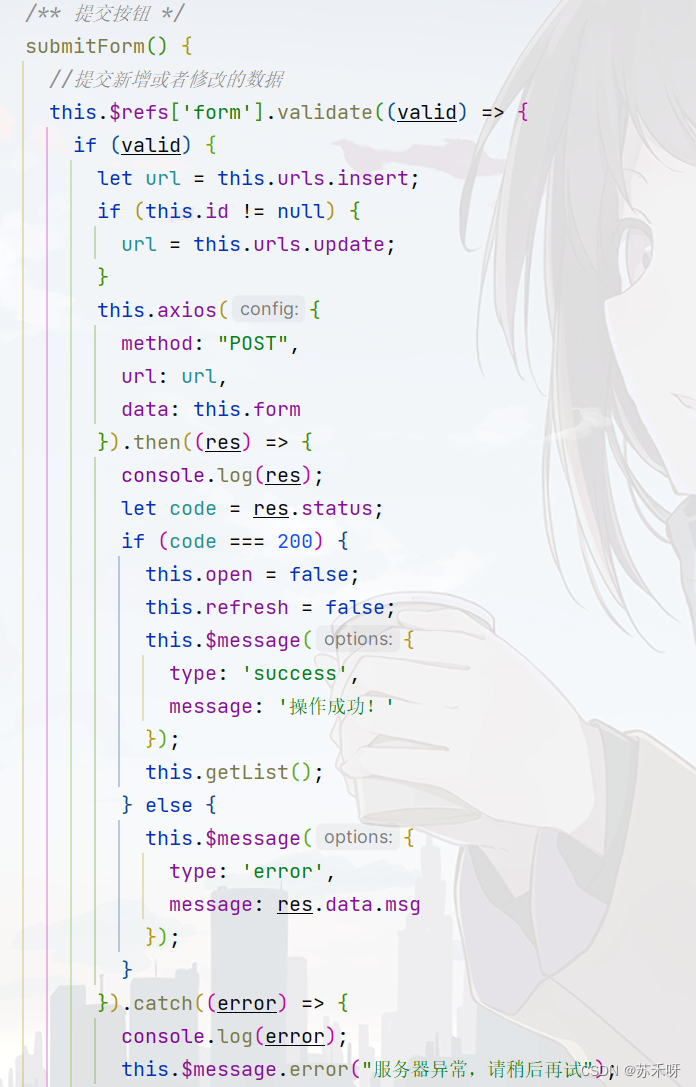
但是在vue3中,实现一个方法需要用到很多文件。

方法定义方法如下:
export function classSign(phone: string) {
return sign_request<Boolean>({
url: `sign?phone=${phone}`,
method: "get"
})
}
export function editBlogCount(data: BolgCountData) {
return sign_request({
url: "blog/blog-info-change",
method: "post",
data
})
} 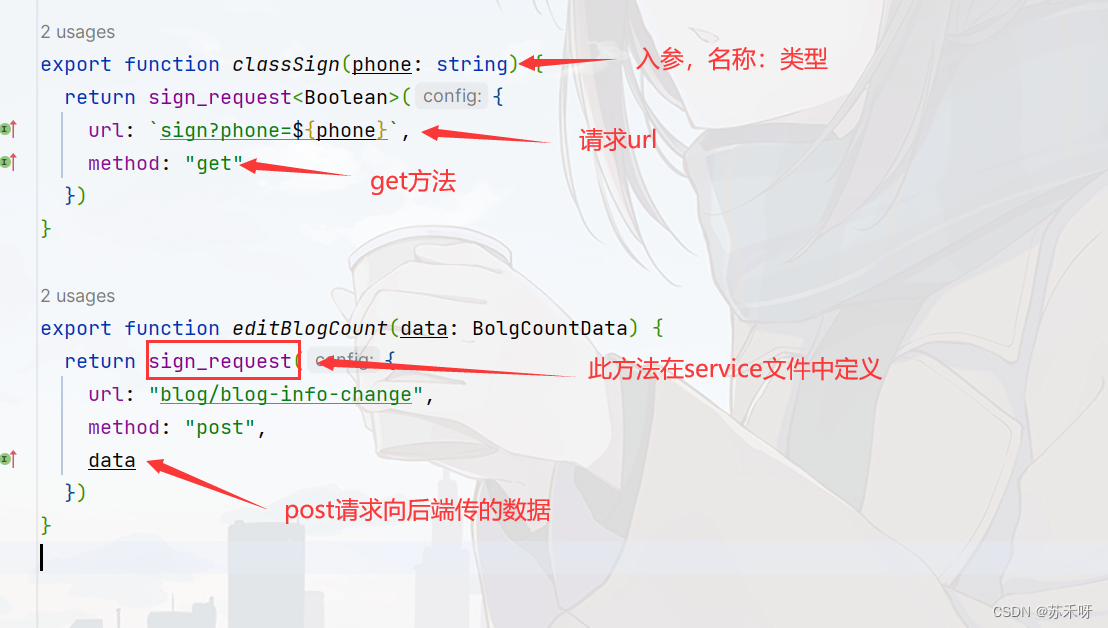
service文件中定义方法
/** 创建请求方法 */
function createRequest(service: AxiosInstance) {
return function <T>(config: AxiosRequestConfig): Promise<T> {
const token = getToken()
const defaultConfig = {
headers: {
// 携带 Token
Authorization: token ? `Bearer ${token}` : undefined,
"Content-Type": "application/json"
},
timeout: 5000,
baseURL: "/sign-system",
data: {}
}
// 将默认配置 defaultConfig 和传入的自定义配置 config 进行合并成为 mergeConfig
const mergeConfig = merge(defaultConfig, config)
return service(mergeConfig)
}
}
/** 用于网络请求的实例 */
const service = createService()
/** 用于网络请求的方法 */
export const sign_request = createRequest(service)
post请求中用到的参数在order.ts中定义:
//入参定义
export interface NoSignStudentList {
id: string
name: string
blogCount: number
blogAddress: string
}
export interface BolgCountData {
phone: string
blogCount: number
}
//出参定义
export type GetTableResponseData = ApiResponseData<{
list: GetTableData[]
total: number
}>
export type GetNoSignData = ApiResponseData<{
noSignStudentListI: NoSignStudentList[]
}>
在vue文件中,首先给按钮绑定点击事件(此处和vue2相同):
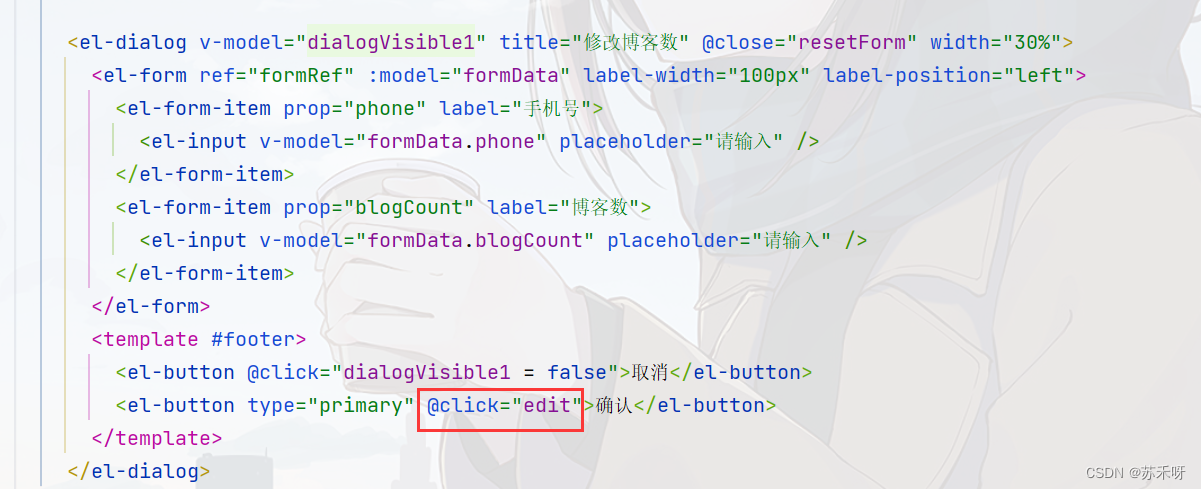
之后在script中定义方法:
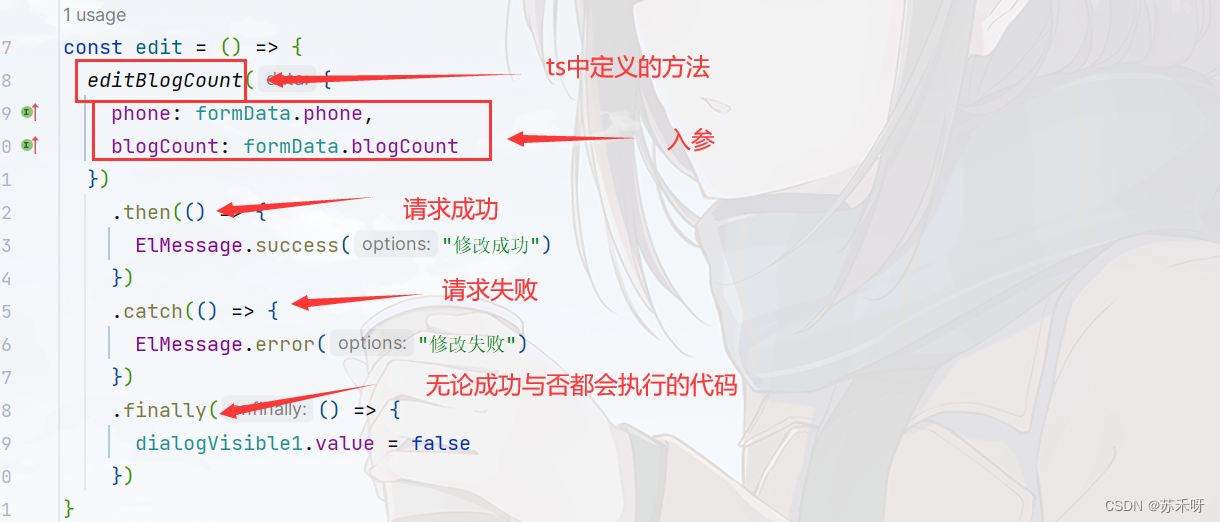
到这里完整的方法就可以实现了,虽然比vue2稍微复杂一点,但是熟练后编写更加方便。