基于串行和并行ADMM算法在分布式调度中的应用（Matlab代码实现）

news2024/11/26 3:53:11

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

2.1 Jacobi

2.2 GS_general

2.3 GS_in_paper

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

参考文献：

目前，国内外学者针对电力流与天然气流协同优化问题已经开展了许多研究。文献［7］建立了一

种考虑安全约束的电—气能量流混合整数规划模型，运用基于线性灵敏因子的迭代算法可同时求解

得到满足 N － 1 约束的电力和天然气网络最优潮流。美国工程院院士 M． Shahidehpour 领导的团队建立了计及天然气网络约束的输电网安全约束机组组合模型，从购气价格、用气需求和输气管道故障等方面分析了天然气系统对电力系统安全经济运行的影响［8-9］。苏黎世联邦理工大学 G． Anderson 教授提出耦合能源中心的多能流网络集成调度方法，采用耦合矩阵和调度因子分别描述能源中心内多能流(如电、气、热)的相互转化和负荷分配［10］。国内清华大学、河海大学等也开展了初步研究工作［11-12］。上述工作通常假定电力与天然气系统垄断运营，由唯一的决策主体(联合调度中心)进行电力流与天然气流的统一优化决策。这种仅含单个决策主体的集中式优化模型与现实中电力和天然气系统一般由不同的运营商负责经营管理并不一致。实际上，两个系统间仅支持少量数据交互，要通过联合调度中心来获得整个电—气互联能源系统的全局信息是相当困难的。这个问题亟须针对电力流与天然气流的实际决策特点———多主体自治决策，运用分布式协同优化手段来解决［13］。

📚2 运行结果

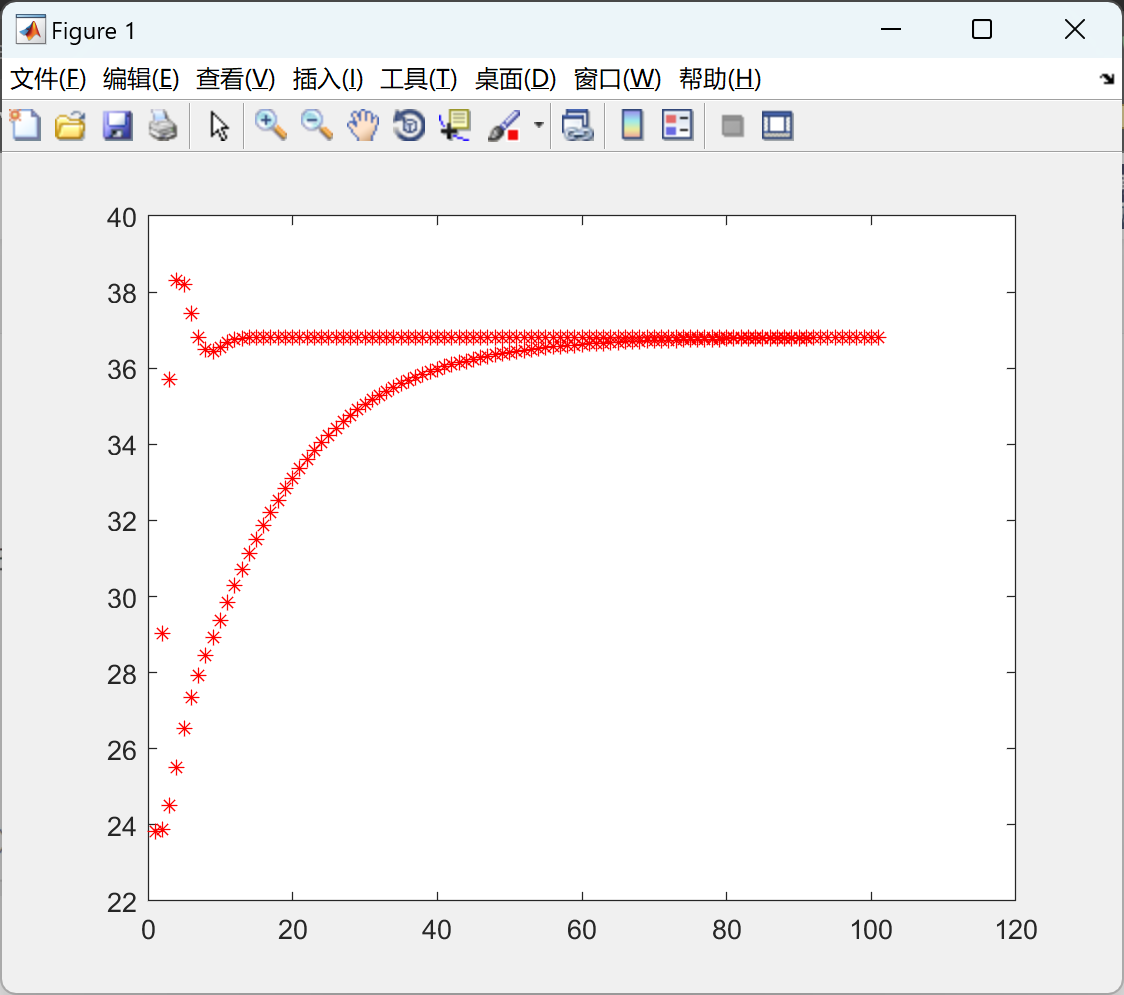
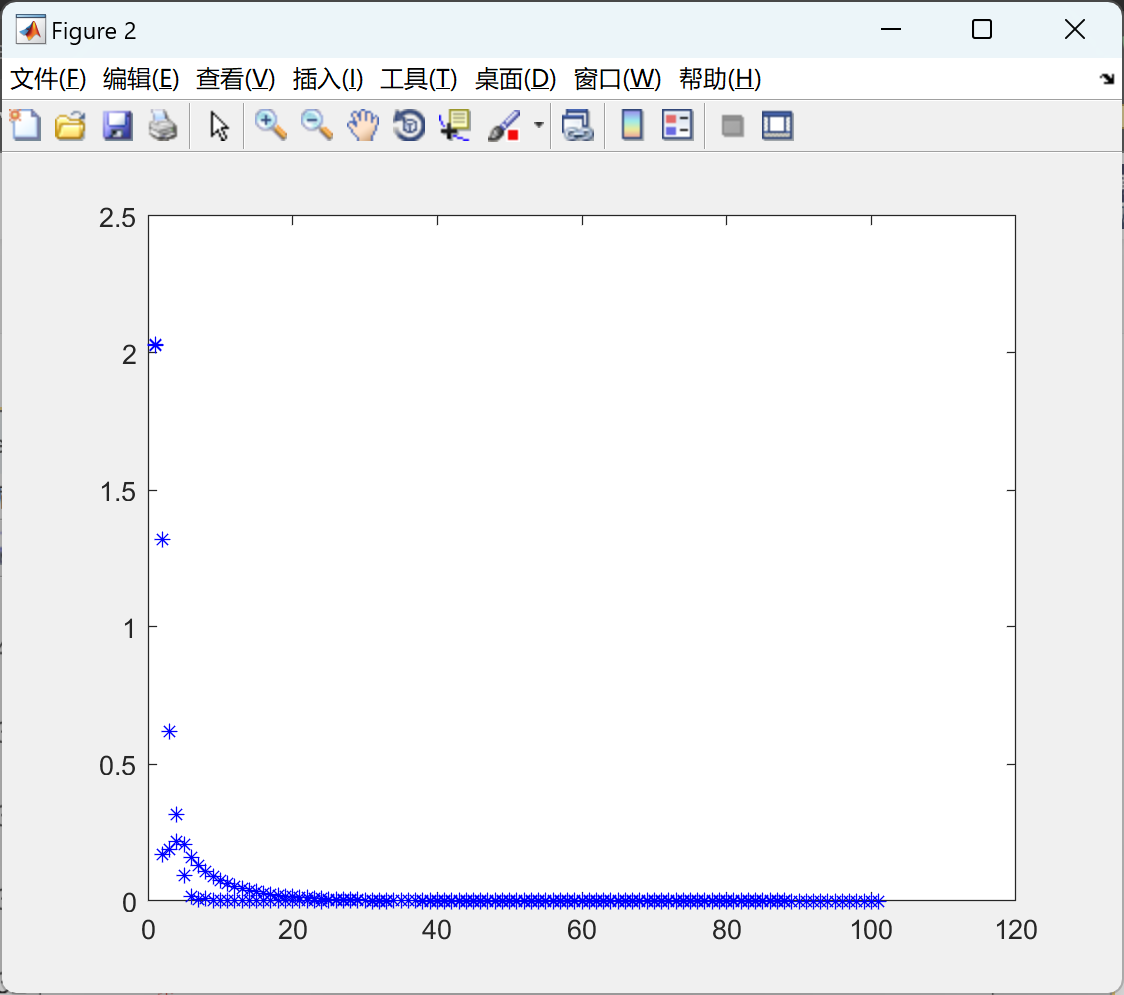
2.1 Jacobi

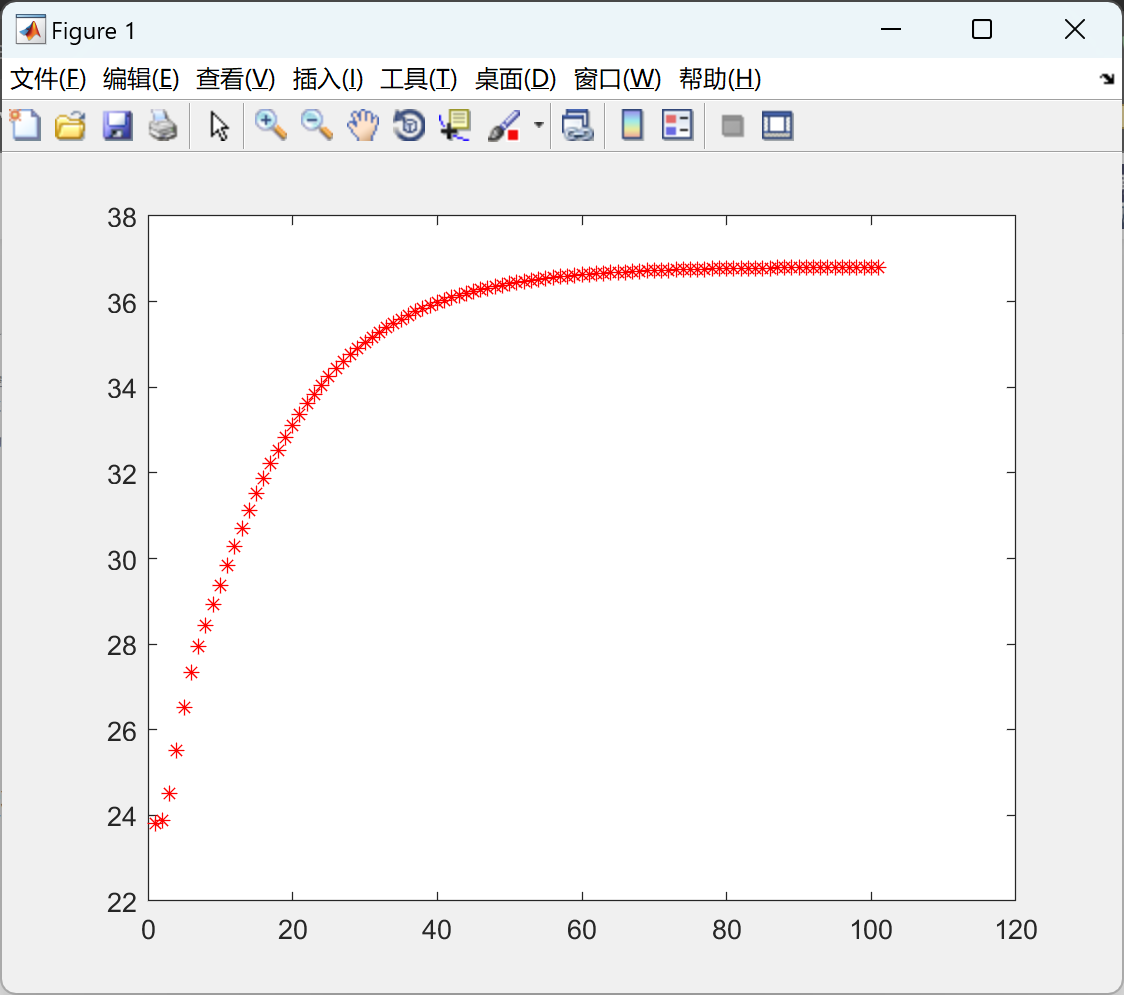
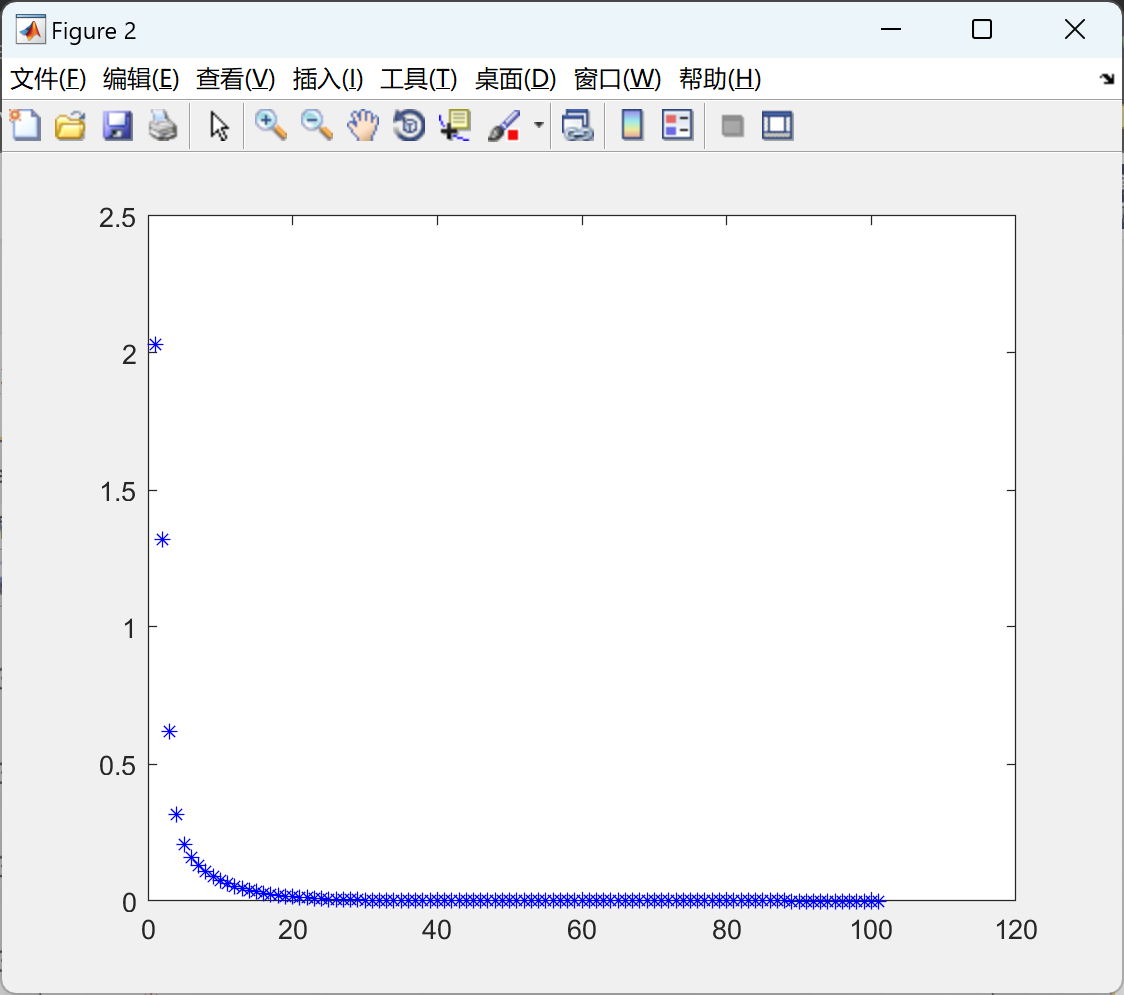
2.2 GS_general

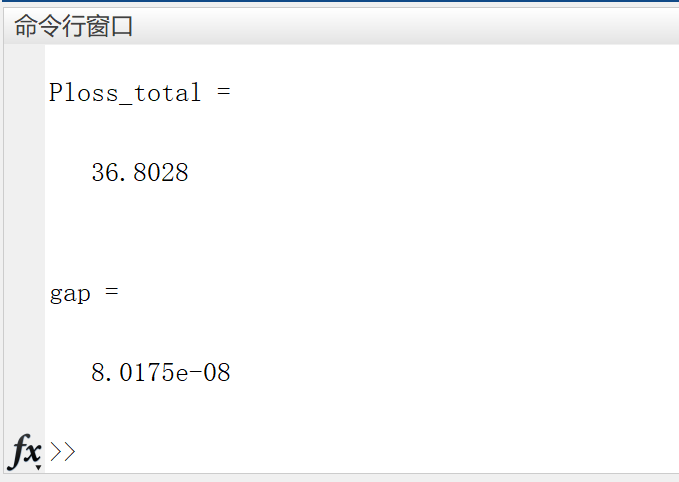
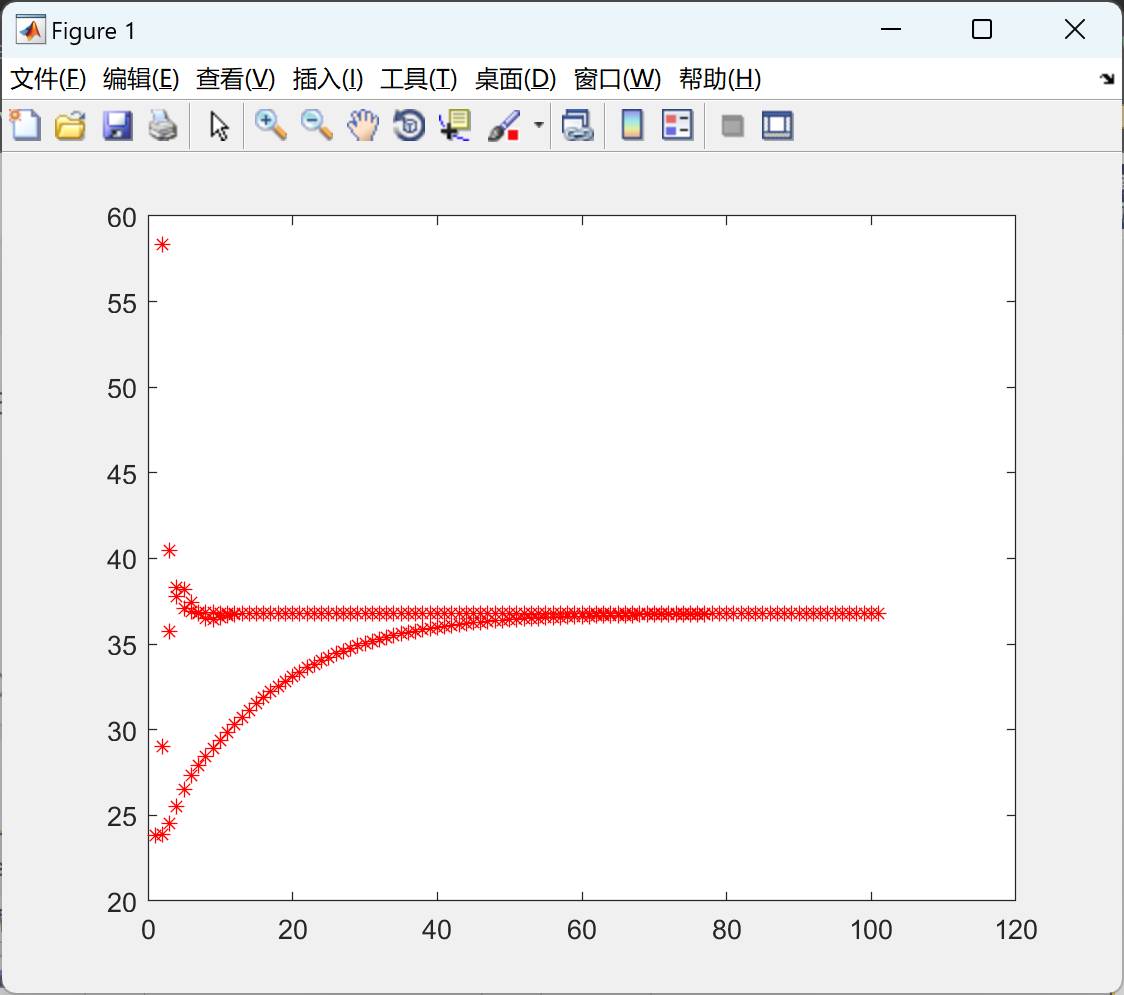
2.3 GS_in_paper

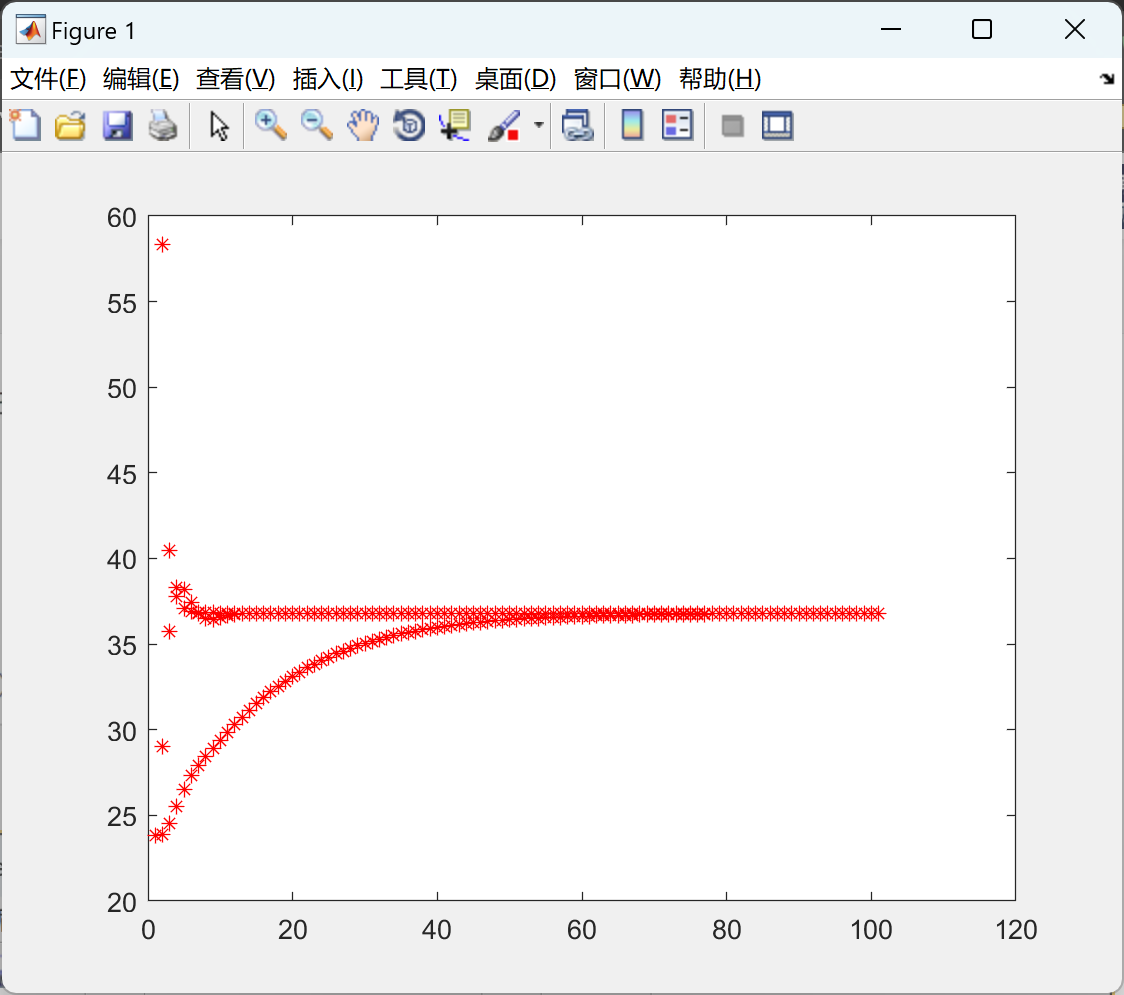
部分代码：

%%ADMM主程序
%%串行计算
clear
clc
%%%区域a,节点33,1-7,18-25
%%耦合为Xa=[U(6),U(7),P(7),Q(7),U(5),U(25),P(25),Q(25)]
Line_a=[1,2,3,4,5,6,7,18,19,20,21,22,23,24,25];
Node_a=[33,1,2,3,4,5,6,18,19,20,21,22,23,24,25];
%%%区域b,节点6-17
%%耦合为Xb=[U(6),U(7),P(7),Q(7)]
Line_b=[7,8,9,10,11,12,13,14,15,16,17];
Node_b=[6,7,8,9,10,11,12,13,14,15,16,17];
%%%区域c,节点5,25-32
%%耦合为Xb=[U(5),U(25),P(25),Q(25)]
Line_c=[25,26,27,28,29,30,31,32];
Node_c=[5,25,26,27,28,29,30,31,32];
%%%%首轮求解
Ploss_data=zeros(32,1);
Volta_data=zeros(33,1);
Qg_data=zeros(33,1);
xigma=0;lagrant_a=[0;0;0;0;0;0;0;0];lagrant_b=[0;0;0;0];lagrant_c=[0;0;0;0];
Xa_last=[0;0;0;0;0;0;0;0];
[Xa,Ploss,Volta,Qg]=program_a(lagrant_a,xigma,Xa_last);
Ploss_data(Line_a)=Ploss(Line_a);Volta_data(Node_a)=Volta(Node_a);Qg_data(Node_a)=Qg(Node_a);
Xb_last=Xa(1:4);xigma=0.1;
[Xb,Ploss,Volta,Qg]=program_b(lagrant_b,xigma,Xb_last);
Ploss_data(Line_b)=Ploss(Line_b);Volta_data(Node_b)=Volta(Node_b);Qg_data(Node_b)=Qg(Node_b);
Xc_last=Xa(5:8);
[Xc,Ploss,Volta,Qg]=program_c(lagrant_c,xigma,Xc_last);
Ploss_data(Line_c)=Ploss(Line_c);Volta_data(Node_c)=Volta(Node_c);Qg_data(Node_c)=Qg(Node_c);
Xa_last=[Xb;Xc];
lagrant_a=lagrant_a+xigma*(Xa-Xa_last);lagrant_b=lagrant_a(1:4);lagrant_c=lagrant_a(5:8);
figure(1)%目标函数
plot(1,sum(Ploss_data),'r*')
hold on
figure(2)%对偶误差
plot(1,norm(Xa-Xa_last,2)^2,'b*-');
hold on
%%%%迭代
for k=1:100
[Xa,Ploss,Volta,Qg]=program_a(lagrant_a,xigma,Xa_last);
Ploss_data(Line_a)=Ploss(Line_a);Volta_data(Node_a)=Volta(Node_a);Qg_data(Node_a)=Qg(Node_a);
Xb_last=Xa(1:4);
[Xb,Ploss,Volta,Qg]=program_b(lagrant_b,xigma,Xb_last);
Ploss_data(Line_b)=Ploss(Line_b);Volta_data(Node_b)=Volta(Node_b);Qg_data(Node_b)=Qg(Node_b);
Xc_last=Xa(5:8);
[Xc,Ploss,Volta,Qg]=program_c(lagrant_c,xigma,Xc_last);
Ploss_data(Line_c)=Ploss(Line_c);Volta_data(Node_c)=Volta(Node_c);Qg_data(Node_c)=Qg(Node_c);
Xa_last=[Xb;Xc];
lagrant_a=lagrant_a+xigma*(Xa-Xa_last);lagrant_b=lagrant_a(1:4);lagrant_c=lagrant_a(5:8);
figure(1)
plot(k+1,sum(Ploss_data),'r*');
figure(2)
plot(k+1,norm(Xa-Xa_last,2)^2,'b*-');
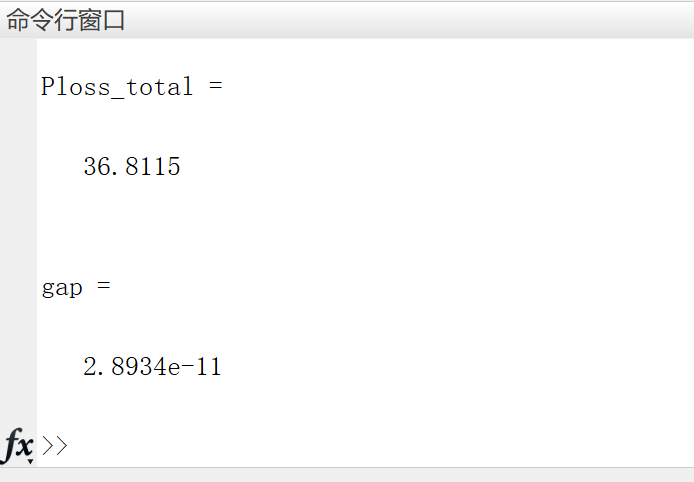
Ploss_total=sum(Ploss_data)
gap=norm(Xa-Xa_last,2)^2
end
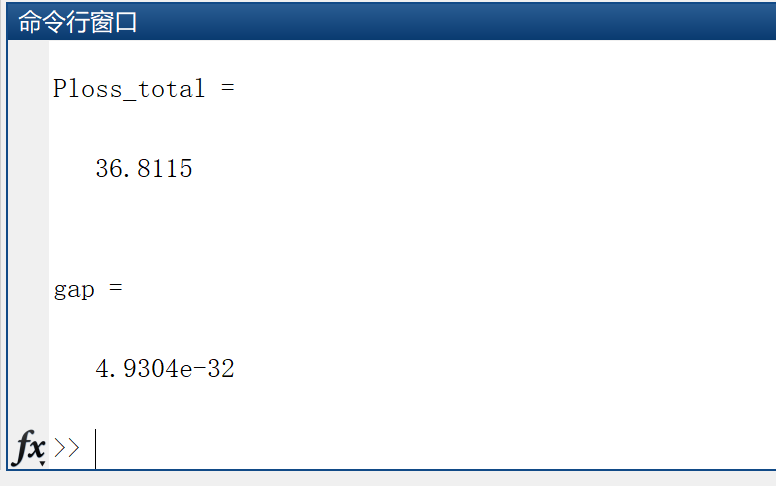
Ploss_total=sum(Ploss_data)
gap=norm(Xa-Xa_last,2)^2