文章目录

环绕字符串中唯一的子字符串
- 题目解析
- 状态转移方程
- 返回值
- 完整代码
最长递增子序列
- 子数组与子序列的区别
- 状态转移方程
- 完整代码
摆动序列
- 题目解析
- 状态转移方程
- - f[i]状态转移方程
  - g[i]状态转移方程
- 完整代码

环绕字符串中唯一的子字符串

点击查看:467. 环绕字符串中唯一的子字符串

定义字符串 base 为一个 “abcdefghijklmnopqrstuvwxyz” 无限环绕的字符串，所以 base 看起来是这样的：
“…zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd…”.
给你一个字符串 s ，请你统计并返回 s 中有多少不同非空子串也在 base 中出现。

示例 1：
输入：s = “a”
输出：1
解释：字符串 s 的子字符串 “a” 在 base 中出现。
示例 2：
输入：s = “cac”
输出：2
解释：字符串 s 有两个子字符串 (“a”, “c”) 在 base 中出现。

题目解析

若以c开头，则可分为 c ca cac
若以a开头，则可分为 a ac
若以最后一个c开头，则可分为c

在环绕字符串中去寻找上述六种字符串，发现只有 c a 符合要求
所以只有两种

状态转移方程

dp[i] 表示以i位置的元素为结尾的所有的子串里面，有多少个在base中出现过

dp[i]分为两种情况

–

情况1：i位置元素本身(长度为1)
在base中包含a-z的所有字母，所以单独一个字母肯定在base中出现
即该情况下长度为1

情况2：i位置元素与前面元素结合(长度大于1)

想要求以i位置的元素为结尾的所有的子串里面，有多少个在base中出现过
就需要先求i-1位置的元素为结尾的所有的子串里面，有多少个在base中出现即dp[i-1]
然后再加上i位置的元素即可
需要保证以 i-1位置为结尾的子串加上i位置元素也要在base中出现

情况1：base是由a到z连续组成
由i-1位置的字符ASCII值+1 即可为i位置的字符的ASCII值即s[i-1]+1==s[i]

情况2：base是由z到a 跳跃组成
i-1位置的字符为z，i位置的字符为a 即s[i-1]==‘z’ && s[i] ==‘a’

两种情况满足一个时，才为符合条件的子字符串

返回值

对于上述字符串，若返回值计算的是dp表的所有值之和
则会计算重复的子串ac ca ,导致结果错误
所以需要去重

两个字符串都是以d字符为结尾的，若都计算就会造成重复
所以当相同字符结尾，将dp值较大的进行累加，将dp值较小的舍去

完整代码

class Solution {
public:
    int findSubstringInWraproundString(string s) {
          int n=s.size();
          //在base中包含a-z的所有字母，所以单独一个字母肯定在base中出现
          //所以将dp表初始化为1
          vector<int>dp(n,1);
         //创建大小为26的数组，用于统计以i位置2为结尾的dp值
         //将dp值大的进行累加 将dp值小的舍去
         //以此达到去重
         vector<int>arr(26,0);
          int i=0;
          int ret=0;
          for(i=1;i<n;i++)
          {
              if(s[i-1]+1==s[i]||s[i-1]=='z'&&s[i]=='a')
              {
                  dp[i]+=dp[i-1];
              }
          }
          //遍历dp表 取其中重复子串的dp最大值
          for(i=0;i<n;i++)
          {
              arr[s[i]-'a']=max(arr[s[i]-'a'],dp[i]);
          }
          for(auto&e:arr)
          {
              ret+=e;
          }
          //返回arr数组的和
          return ret; 
    }
};

最长递增子序列

点击查看:300. 最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
示例 2：
输入：nums = [0,1,0,3,2,3]
输出：4

子数组与子序列的区别

子序列：按照从左到右的顺序，任意挑选几个所组成的新序列即为子序列
如：a b d 为子序列跳过了c ，但相对顺序与原数组保持一致(d在原数组中就在a b后，新的数组也是如此)
而 d a b 就不是一个子序列了

子数组：按照从左到右的顺序，任意挑选的必须是连续的
如：a b c为子数组，但 a b d就不是子数组

状态转移方程

dp[i] 表示以i位置元素为结尾的所有的子序列中，最长的递增子序列的长度

dp[i]分为两种情况

情况1：i位置元素本身(长度为1)
只有i位置元素本身，所以该情况下最长的递增子序列的长度为1

情况2：i位置元素和前面元素结合(长度大于1)

想要求以i位置元素为结尾的所有的子序列中，最长的递增子序列的长度
就需要先求区间[0,i-1]内的最长的递增子序列的长度(因为子序列是相对顺序所以有可能不在i-1位置取最长长度)
( 假设区间[0,i-1]为j)
再加上i位置元素长度即+1

由于是递增子序列，就需要使j位置的元素小于i位置元素
即 nums[j]<nums[i]

由于j是一个区间，所以在区间内寻找最大值
即 dp[i]= max(dp[j]+1)

完整代码

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        //由于最差的情况是取i位置元素本身 即最长的递增长度为1
        //所以初始化为1
        vector<int>dp(n,1);
        int i=0;
        int j=0;
        for(i=1;i<n;i++)
        {
            for(j=0;j<i;j++)
            {
                //再保证是一个递增子序列的情况下
                if(nums[j]<nums[i])
                {
                   dp[i]=max(dp[i],dp[j]+1);
                }
            }
        }
        int ret=INT_MIN;
        //遍历dp表寻找最大值
        for(i=0;i<n;i++)
        {
          ret=max(ret,dp[i]);
        }
        //返回dp表最大值
        return ret;
    }
};

摆动序列

点击查看:376. 摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如， [1, 7, 4, 9, 2, 5] 是一个摆动序列，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。
给你一个整数数组 nums ，返回 nums 中作为摆动序列的最长子序列的长度。

示例 1：
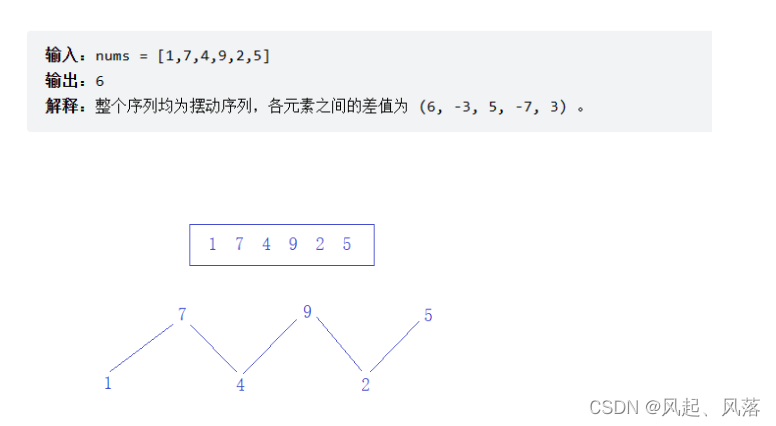
输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

题目解析

正常情况下，每次需要保证一上一下才能为摆动序列

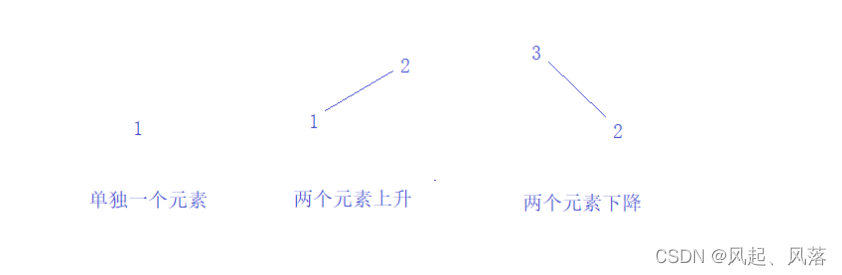
单独一个元素也视为摆动序列
或者两个元素不相等，也被视为摆动序列

状态转移方程

dp[i]：表示以i位置为结尾的所有子序列中，最长的摆动序列的长度

f[i]：表示以i位置为结尾的所有子序列中，最后一个位置呈现上升趋势的最长的摆动序列的长度

g[i]：表示以i位置为结尾的所有子序列中，最后一个位置呈现下降趋势的最长的摆动序列的长度

f[i]状态转移方程

情况1：i位置元素本身(长度为1)
单独一个元素可以为一个摆动序列，即最长的摆动序列的长度为1

情况2：i位置元素与前面元素集结合(长度大于1)

想要求以i位置元素为结尾的所有的子序列中，最后一个位置呈现上升趋势的最长的摆动序列的长度
就需要先求区间[0,i-1]内的最后一个位置呈现下降趋势的最长的摆动序列的长度(因为子序列是相对顺序所以有可能不在i-1位置取最长长度)
( 假设区间[0,i-1]为j)
再加上i位置元素长度即+1
即g[j]+1
由于j是一个区间，所以取区间中的最大值即 f[i]=max(g[j]+1,f[i]);

最后一个位置呈现上升趋势，就需要加上限制条件：使j位置的元素小于i位置元素
即 nums[j]<nums[i]

g[i]状态转移方程

情况1：i位置元素本身(长度为1)
单独一个元素可以为一个摆动序列，即最长的摆动序列的长度为1

情况2：i位置元素与前面元素集结合(长度大于1)

想要求以i位置元素为结尾的所有的子序列中，最后一个位置呈现下降趋势的最长的摆动序列的长度
就需要先求区间[0,i-1]内的最后一个位置呈现上升趋势的最长的摆动序列的长度(因为子序列是相对顺序所以有可能不在i-1位置取最长长度)
( 假设区间[0,i-1]为j)
再加上i位置元素长度即+1
即f[j]+1
由于j是一个区间，所以取区间中的最大值即 g[i]=max(f[j]+1,g[i]);

最后一个位置呈现下降趋势，就需要加上限制条件：就需要使j位置的元素大于i位置元素
即 nums[j]>nums[i]

完整代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
     int n=nums.size();
     //创建f表(最后一个位置呈现上升趋势)
     //g表(最后一个位置呈现下降趋势)j
     vector<int>f(n,1);
     vector<int>g(n,1);
     int i=0;
     int j=0;
     //只有一个元素时也为摆动序列 所以最低长度为1
     int ret=1;
     for(i=1;i<n;i++)
     {
           for(j=0;j<i;j++)
           {
               //在保证j位置元素小于i位置元素
              if(nums[j]<nums[i])
              {
                  f[i]=max(g[j]+1,f[i]);
              }
              //在保证j位置元素大于i位置元素
              if(nums[j]>nums[i])
              {
                  g[i]=max(f[j]+1,g[i]);
              }
           }
           //取f表和g表中的最大值
           ret=max(max(ret,f[i]),g[i]);
     }
     //返回f和g表 两者中的最大值
     return ret;
    }
};