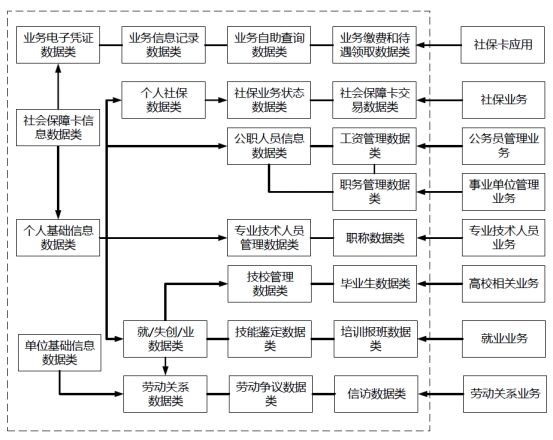
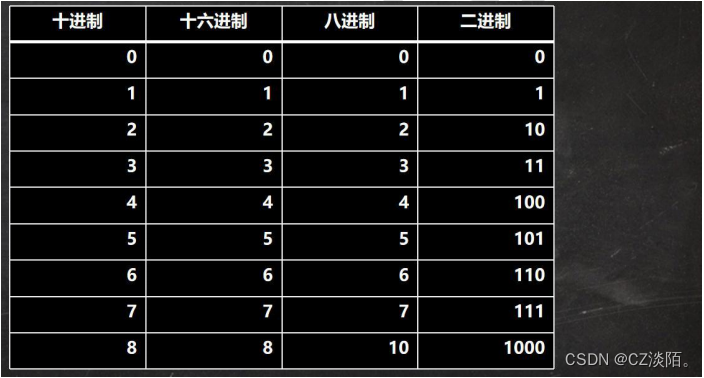
进制

进制介绍

对于整数，有四种表示方式：
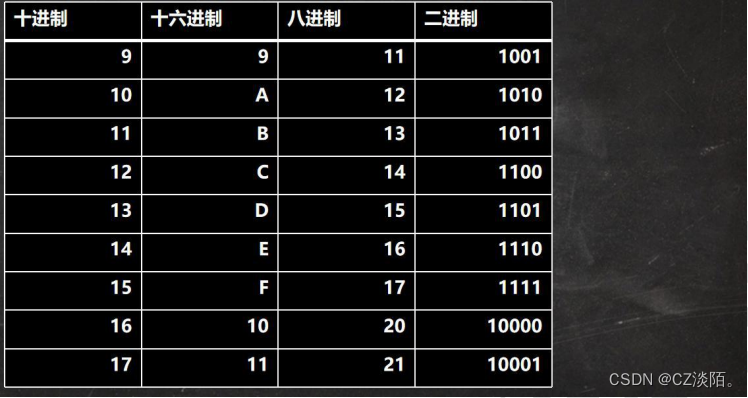
二进制：0,1 ，满 2 进 1.以 0b 或 0B 开头。
十进制：0-9 ，满 10 进 1。
八进制：0-7 ，满 8 进 1. 以数字 0 开头表示。
十六进制：0-9 及 A(10)-F(15)，满 16 进 1. 以 0x 或 0X 开头表示。此处的 A-F 不区分大小写。

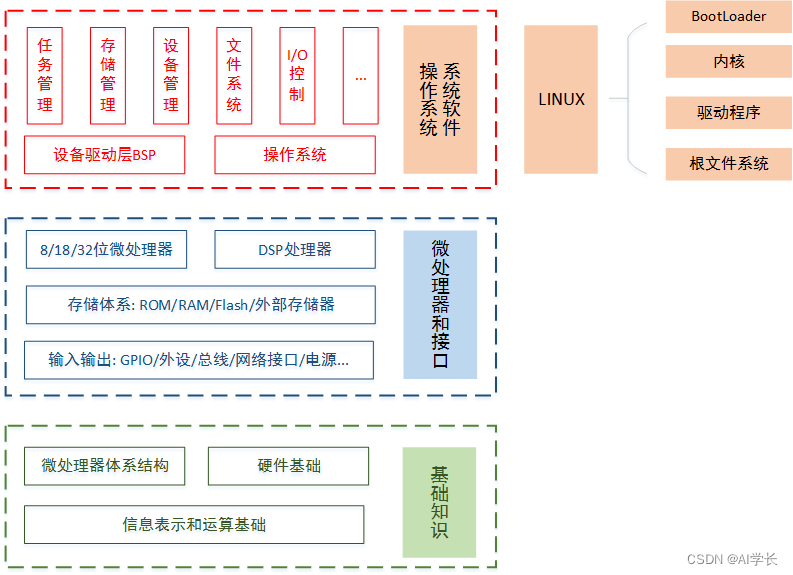
进制的图示

进制的转换

进制转换的介绍

第一组：

1. 二进制转十进制
2. 八进制转十进制
3. 十六进制转十进制

第二组：

1. 十进制转二进制
2. 十进制转八进制
3. 十进制转十六进制

第三组

1. 二进制转八进制
2. 二进制转十六进制

第四组

1. 八进制转二进制
2. 十六进制转二进制

二进制转换成十进制示例

八进制转换成十进制示例

十六进制转换成十进制示例

规则：从最低位(右边)开始，将每个位上的数提取出来，乘以 16 的(位数-1)次方，然后求和。
案例：请将 0x23A 转成十进制的数
0x23A = 10 * 16^0 + 3 * 16 ^ 1 + 2 * 16^2 = 10 + 48 + 512 = 570

十进制转换成二进制

规则：将该数不断除以 2，直到商为 0 为止，然后将每步得到的余数倒过来，就是对应的二进制。
案例：请将 34 转成二进制 = 0B00100010

十进制转换成八进制

规则：将该数不断除以 8，直到商为 0 为止，然后将每步得到的余数倒过来，就是对应的八进制。
案例：请将 131 转成八进制 => 0203

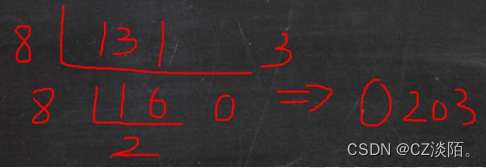
十进制转换成十六进制

规则：将该数不断除以 16，直到商为 0 为止，然后将每步得到的余数倒过来，就是对应的十六进制。
案例：请将 237 转成十六进制 => 0xED

二进制转换成八进制

规则：从低位开始,将二进制数每三位一组，转成对应的八进制数即可。
案例：请将 ob11010101 转成八进制
ob11(3)010(2)101(5) => 0325

二进制转换成十六进制

规则：从低位开始，将二进制数每四位一组，转成对应的十六进制数即可。
案例：请将 ob11010101 转成十六进制
ob1101(D)0101(5) = 0xD5

八进制转换成二进制

规则：将八进制数每 1 位，转成对应的一个 3 位的二进制数即可。
案例：请将 0237 转成二进制
02(010)3(011)7(111) = 0b10011111

十六进制转换成二进制

规则：将十六进制数每 1 位，转成对应的 4 位的一个二进制数即可。
案例：请将 0x23B 转成二进制
0x2(0010)3(0011)B(1011) = 0b001000111011