目标跟踪基础：数据关联算法

本文来自公众号“AI大道理”

——————

数据关联是多目标跟踪任务中的关键步骤，其目的主要是为了进行帧与帧之间的多个目标的匹配。

1、数据关联

数据关联其实就是一个沿着时间轴，将来自同一个物体的不同时刻的信号串联起来的过程。

数据关联通常在状态估计之前进行，只有获得准确的数据关联处理结果，才能保证后续处理的正确性。

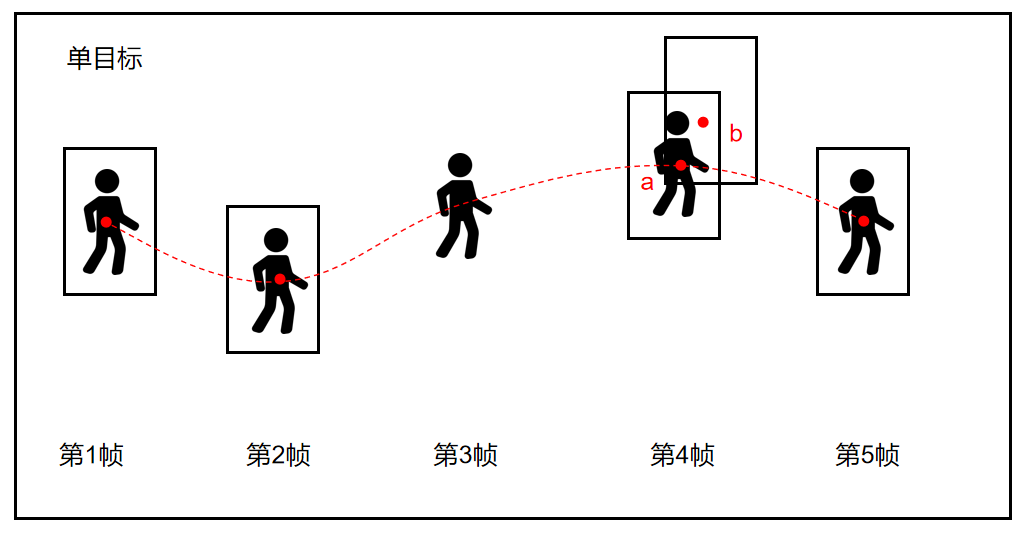
一个人行走的轨迹，第三帧漏检，导致没有检测框，第四帧误检，导致一个干扰框。

第四帧中有一个检测结果是错的，此时就是涉及到了数据关联，关联匹配我们收到的检测结果和真实目标。

也就是说数据关联就是确保a框关联或者匹配到人（ID:1）上，而不是猫上，也确保误检的框或者猫的框不要给到这个人。

之后的状态估计靠传统卡尔曼滤波器和其变体基本上可以解决。

（灵魂的拷问：对于第四帧，我们怎么确定哪个结果是错的？）

传统的数据关联算法，第一个功能就是提供了怎么算这个概率的方法，最最简单的是最近邻（NN），就是探测结果离我们自己理论预测的结果越近，概率越大。然后我们就挑这个概率最大的结果。

2、数据关联算法

数据关联算法：

基于IOU的贪婪匹配
最近邻算法（Nearest Neighbor，NN）
概率数据关联（Probability Data Association，PDA）
联合概率数据关联（Joint Probability Data Association，JPDA）
匈牙利算法（Hungarian Algorithm）
KM算法（Kuhn-Munkres Algorithm）
数据关联网络（Data Association Neural Networks）

3、基于IOU的贪婪匹配

IOU Tracker的跟踪方式没有跟踪，只有数据关联，关联指标就是IOU，关联算法就是一种基于IOU的贪婪匹配算法。

基于贪婪算法的数据关联的核心思想就是，不考虑整体最优，只考虑个体最优。

距离度量：IOU

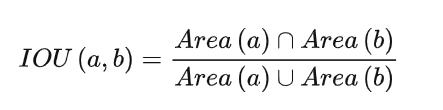
关联算法：依次关联

依次为每条跟踪轨迹分配观测量，即计算前一帧检测框和当前帧的所有检测框的IOU，只要某个框的IOU满足指标或者最大，则将这个框与之关联。

但前提是不能漏检，一旦出现漏检，匹配上的框必然是错误的，或者匹配不上。

由于IOU Tracker仅仅是对观测量进行了关联，当目标丢失或者检测不到的时候，便无法重建轨迹。

因此V-IOU加入了KCF单目标跟踪器来弥补这一漏洞。

4、最近邻算法

最近邻算法（Nearest Neighbor Algorithm）是最常见的数据关联算法之一，基于距离度量（如欧氏距离、马氏距离等），将当前帧中的目标与先前帧中的已跟踪目标进行匹配。

距离度量：欧式距离

关联算法：依次关联

相当于计算前一帧检测框和当前帧所有检测框的距离，距离近的就关联上。

最近邻算法通常选择距离最小的目标作为匹配对象。

近邻算法是最简单的数据关联技术，通过设定阈值来聚类最相近的一组值。

但是近邻算法在密集环境中性能较差，人挤人的情况下框的距离将会差不多，容易关联错误。

全局最近邻算法：

最近邻算法存在多个目标关联到同一个测量结果的情况，即有的测量结果对于多个目标来说都是它们最近关联。

全局最近邻计算所有可能的关联情况，选用总距离或者说总概率最大的关联方式，从而避免了上述情况的发生。

5、概率数据关联算法

概率数据关联为一个目标的一次有效测量的的每一个可能性设置一个关联概率。

有效测量定义为观测值在当前时刻处于目标的有效门限内。

在概率数据关联算法中，目标的状态估计是由在所有情形下预测状态的加权和得到的。

算法能够将一个特定目标的不同测量值关联起来。

因此，关联对于一个目标的不同测量结果能够更好地估计目标的状态。

概率数据关联算法（Probabilistic Data Association Algorithm，简称PDA）通过考虑多个观测对应于同一目标的概率，以概率的形式进行目标关联。它基于贝叶斯滤波的框架，将目标的状态估计表示为概率分布，通过观测来更新和修正目标状态的概率。

概率数据关算法的基本思想：

在每个时刻，对于每个传感器观测，计算其与每个已知目标的关联概率。然后，根据关联概率和每个目标的预测概率，对目标状态进行更新和修正。PDA算法还考虑了观测误差和目标运动的不确定性，以及观测与目标的关联可能性。

PDA算法在多目标跟踪中具有较好的性能，特别是在存在目标遮挡、观测噪声和数据关联不确定性的复杂场景中。它可以提供目标状态的概率估计，对不确定性进行建模，并能够处理观测缺失和错误关联的情况。

需要注意的是，PDA算法的计算复杂度较高，尤其在目标数量较多和观测空间较大的情况下。

6、联合概率数据关联

联合概率数据关联是一种非最优的，在密集环境中跟踪多目标的方法。

联合概率数据关联与概率数据关联相似，但是联合概率数据关联的关联概率是由所有目标的所有观测值计算得到。

因此，联合概率数据关联考综合考虑了多个可能并进行了组合。

联合概率数据关联有以下约束：

一个测量值只能来自一个目标；
两个测量值在同一时刻不可能来自同一个目标；
同一个目标的测量概率之和为1；

联合概率数据关联有以下缺点：

需要一个明确的机制来进行轨迹的初始化，和概率数据关联一样，联合概率数据关联不能新建或移除观测区域之外的轨迹。

联合概率数据关联在处理多目标时计算量很大因为假设的数量随目标的数量指数增长。

7、匈牙利算法基础

依次进行数据关联是局部最优解，并不能代表全局最优解。

而匈牙利算法则在追求全局最优，是一种在多项式时间内求解分配问题的组合优化算法。

多目标跟踪数据关联问题可以转化为有权二分图最小权匹配问题，匈牙利算法就是解决数据关联问题的图算法。

图：

图（Graph，G），是由顶点集合（Vertices，V）和边集合（Edges，E）组成的二元组，表征了不同顶点间的拓扑连接关系，记作：

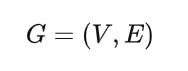
图中的边是否具有单向性可将图分为有向图和无向图，根据图中的边是否具有不同的权重可将图分为有权图和无权图。

二分图：

二分图（Bipartite Graph）是一种特殊的图，又称二部图。

二分图的顶点集可以被划分为两个互不相交的独立子集U和V。

二分图边集合 E 中的每一条边分别连接了顶点子集 U 和 V 中的一个顶点，但 U 和 V 内部的顶点互不相连。

二分图的结构与多目标跟踪任务的结构很相像，可以把U与V看成是多目标跟踪任务中的前一帧与当前帧的检测框集合，U与V之间的关联视为前一帧与当前帧的同一id目标的检测框的关联，我们需要做的就是将相邻两帧的目标检测框尽可能准确的两两匹配。

匹配：

给定图G=(U，V，E)，一个匹配表示多个U和多个V之间的关联M。

M是E的一部分，即子集。

匹配不仅仅是两个点一条线，而是多个关联的组合。

匹配是一种关联的方案。

匹配中的线是一一对应的，是一个点链接另外一个点的，在目标检测中就是当前帧的检测框一一对应到上一帧的检测框。

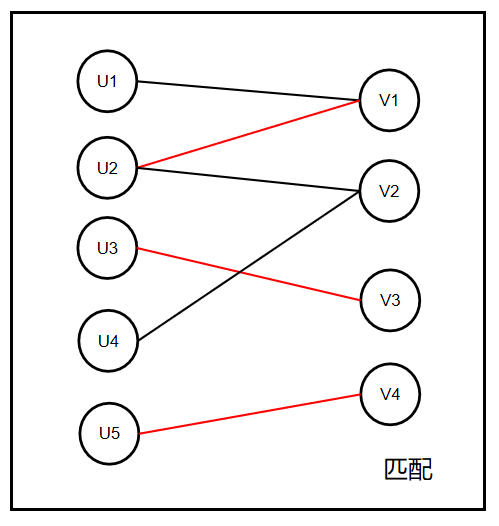
如下图的U5和V4，U3和V3，U2和V1共同组成一个匹配。

匹配上的边叫匹配边，未匹配上的边叫未匹配边。

同样的，匹配上的点叫匹配点，未匹配上的点叫未匹配点。

最大匹配：

最大匹配（Maximum-Cardinality Matching）表示图的所有匹配中边数最多的匹配方案，最大匹配不唯一。

匹配边数最大值就是一个集合点的个数。

大权匹配：

对于有权图而言，最大权匹配（Maximum-Weight Matching）表示的是有权图的所有匹配中边的权重之和最大的那些匹配。

最小权匹配：

对于有权图而言，最小权匹配（Minimum-Weight Matching）表示的是有权图的所有匹配中边的权重之和最小的那些匹配。

多目标跟踪数据关联问题可以转化为有权二分图最小权匹配问题。

跟踪过程中的上一帧目标可以看成U，下一帧目标可以看做V，边的权重可以看作是上一帧目标和下一帧目标通过某种方式计算得到的匹配距离，这个匹配距离我们称之为代价（Cost），所有的匹配距离构成了代价矩阵（Cost Matrix），我们要找到匹配关系使得总的匹配距离最小（代价最低）。

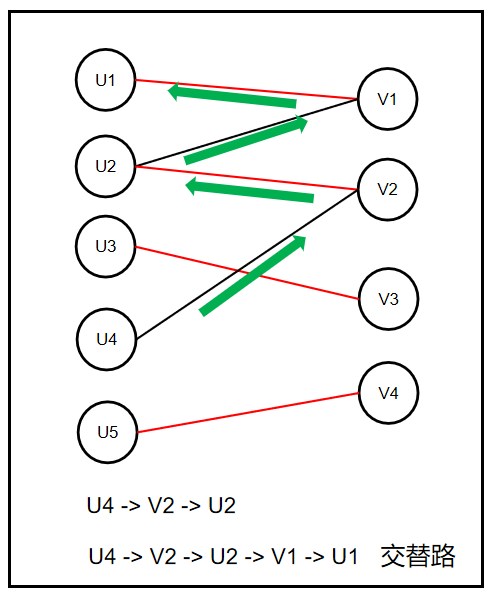
交替路：

交替路从某个未匹配点出发，交替经过未匹配边和匹配边形成的路径。

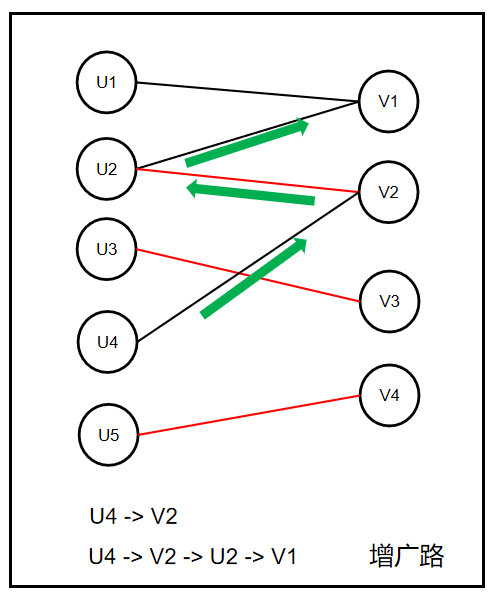
增广路：

增广路（Augmenting Path）是一条特殊的交替路，增广路从图中的某个未匹配点起始，交替经过未匹配边和匹配边，并终止于不同于起始点的另一个未匹配点。

性质：

Berge 定理：对于给定的图G和它的一个匹配M，M是G的最大匹配的充要条件是G中不存在匹配M的增广路。
增广路上的边个数一定是奇数，是奇数就意味着是一边的点到另外一个的点。这样增广路上的边未匹配的边一定比匹配边多1。

如何找到最大权匹配？

对于一个给定的二分图 G=(U,V,E)和初始为空的匹配M，只要反复搜索增广路就能逐渐扩展匹配的大小，最终当我们找不到增广路时就得到了一个最大匹配。

利用增广路找最大匹配的算法，就叫做匈牙利算法。

8、匈牙利算法

匈牙利算法（Hungarian Algorithm），也称为Kuhn-Munkres算法，是一种解决指派问题（Assignment problem）的优化算法。指派问题是在给定的任务和资源之间建立最佳的一对一分配关系的问题。

具体来说，匈牙利算法解决的是一个二维的代价矩阵，其中每个元素表示将一个任务分配给一个资源的成本或代价。算法的目标是找到一种分配方式，使得总成本最小。

匈牙利算法的基本思想是通过不断寻找增广路径来找到最佳的分配方式。

匈牙利算法步骤：

步骤1：代价矩阵德每一行减去改行的最小值。

步骤2：代价矩阵德每一列减去该列的最小值。

步骤3：用尽量少的线覆盖矩阵中所有的0，判断线的数量是否小于n（矩阵行数列数）

步骤4：线的数量小于n，则需要继续减，未被线覆盖的行或者列继续减掉未被覆盖的最小值，被线覆盖一次的不参与减，被线覆盖两次的反而要加这个最小值。

步骤5：重复上面步骤4，直到找到线的个数等于n，则得到最终的匹配方案。

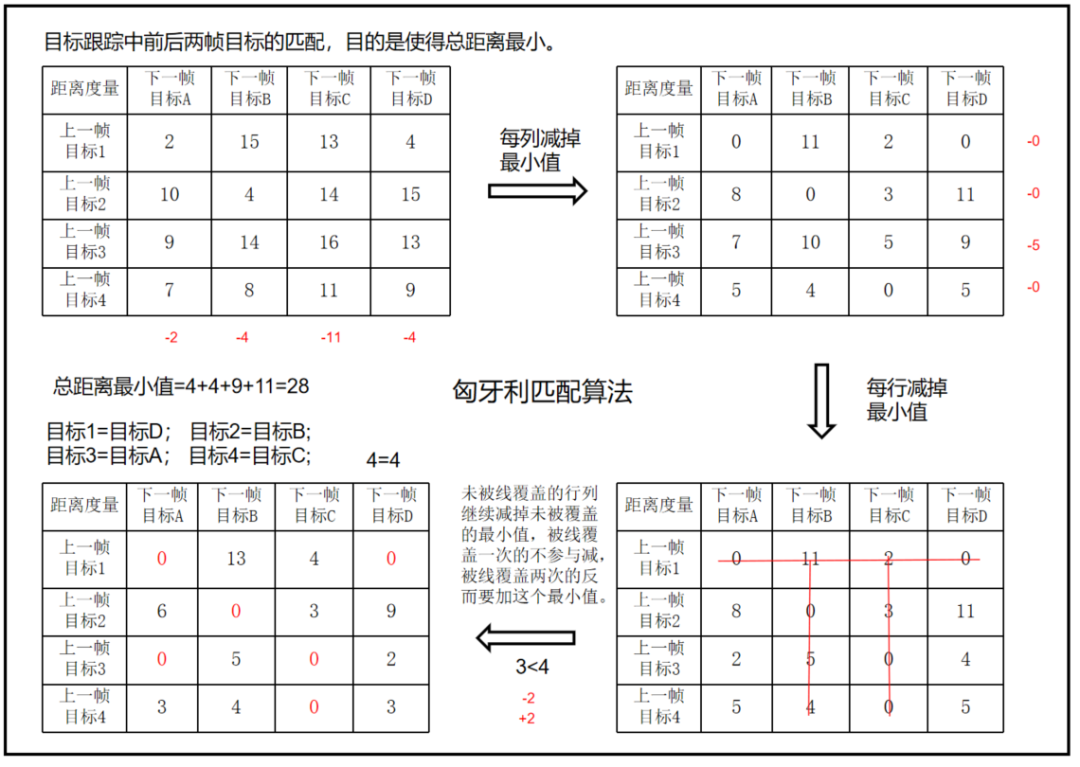
最后需要划 4 条线才能覆盖住矩阵中所有的 0 元素，迭代终止，根据矩阵中 0 元素的位置很容易得到最终的匹配关系：目标1→目标D，目标2→目标B，目标3→目标A，目标4→目标C。

这个匹配满足构成的二分图上的匹配边总权重最小，即总的匹配距离最小，代价最低。

若目标和下一帧目标个数不一致，则需要补0进行匈牙利算法。

假设不用匈牙利算法进行匹配，而是按照顺序进行局部最小值匹配。

显然不是最优匹配。

9、KM算法

现在常说的以及文献中常提到的匈牙利算法和 Kuhn-Munkres 算法指的是同一个东西，求解的都是有权二分图最小权匹配问题；

James Munkres 引入了“标星 0（starred zeros）”和“标撇 0（primed zeros）”的概念以改进匈牙利算法原始流程中的划线法，在算法执行过程中会选择性地对代价矩阵中产生的 0 元素标记星号（*）或标记撇号（’）来辅助搜索增广路，标星 0 表示增广路中的匹配边，标撇 0 表示增广路中的未匹配边。

可以说KM算法是对匈牙利算法进行了改进和推广。

后来习惯将 Munkres 提出的方法称为 Kuhn–Munkres 算法、KM 算法或 Munkres 分配算法。

匈牙利算法与KM算法傻傻分不清楚：

有一种观点认为匈牙利算法是不带权重的，只用于在图中寻找最大匹配。而KM算法是用于带权重的匹配，求解过程中包含匈牙利算法。若是此观点，则上述目标跟踪匹配例子其实应该叫KM算法，因为距离度量就是权重。

而另外一种观点则是匈牙利算法（Hungarian Algorithm），也称为Kuhn-Munkres算法，是同一种算法的不同叫法。本文遵循此观点。

10、数据关联网络

数据关联神经网络（Data Association Neural Network）是一种利用神经网络进行数据关联的方法。

在目标跟踪、目标识别和多目标追踪等任务中，数据关联是指将观测到的目标与已知的目标进行关联，以确定它们之间的对应关系。

传统的数据关联方法通常依赖于启发式规则、距离度量或最大后验概率等方法。

而数据关联神经网络通过学习数据之间的关联模式，从数据中自动学习和推断目标之间的关联关系。

数据关联神经网络通常由两个主要组成部分组成：

特征提取网络（Feature Extraction Network）：该网络用于从输入的数据中提取有意义的特征。它可以是卷积神经网络（Convolutional Neural Network，CNN）或其他适用于特定任务的网络。
关联网络（Association Network）：该网络用于学习目标之间的关联关系。它接收从特征提取网络提取的特征，并使用神经网络的模型进行目标之间的关联计算。关联网络可以是全连接神经网络、循环神经网络（Recurrent Neural Network，RNN）或其他适用的网络结构。

数据关联神经网络的训练通常涉及到大量的标注数据，其中包含了观测目标和已知目标之间的对应关系。通过反向传播算法和适当的损失函数，网络可以学习到使目标之间的关联最优化的参数设置。

数据关联神经网络能够自动学习数据中的关联模式，具有较强的表达能力和泛化能力，并且可以适应不同的任务和数据类型。