如果有兴趣了解更多相关内容，欢迎来我的个人网站看看：瞳孔空间

一：分类与预测

分类(Classification)：分类是找出描述并区分数据类或概念的分类函数或分类模型(也常常称作分类器)，该模型能把数据库中的数据项映射到给定类别中的某一个，以便能便用模型预测类标记未知的对象类。

• 目的：预测种类类别标识(离散型)
• 常规步骤：基于训练数据集(其史每个对象县有明确的类别标识)形成一个分类模型，然后用分类模型对新的数据进行分类
• 典型应用：医疗诊断，模式识别

预测(Prediction)：识别对象在特定时刻的状态（带有时间参数的求解）

• 过程：首先对数据拟合模型(通常是连续的属性值函数），然后对新数据进行预测
• 典型应用：信用度评估、市场分析、方案效果分析

分类的步骤(1)：建立模型

分类的步骤(2)：使用模型进行预测

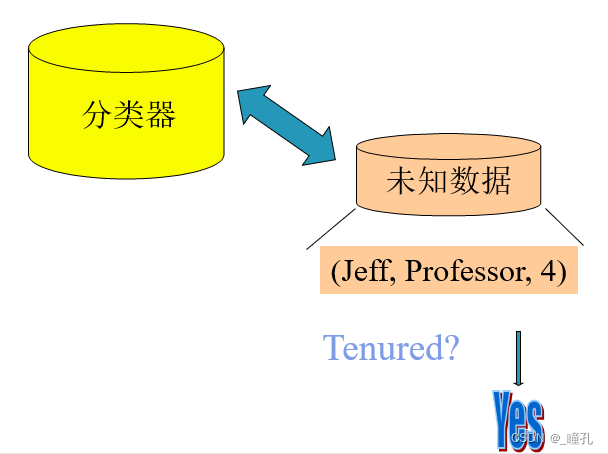
分类与预测的案例：

• 市民出行选乘公交预测：挖掘固定人群在公共交通中的行为模式，分析推测乘客出行习惯和偏好
• 商品图片分类：京东等“拍照购”“找同款”等
• 监控场景下的行人精细化识别：基于监控场景下带有标注信息的行人图像，在定位（头部、上身、下身、脚、帽子、包）的基础上研究行人精细化识别算法，自动识别出行人图像中行人的属性特征

分类器评价或比较尺度：

• 预测准确度：
  • 保持(holdout)
  • K-次交叉验证(k-fold cross validation)
• 计算复杂度：空间和时间的复杂度
• 模型描述的简洁度

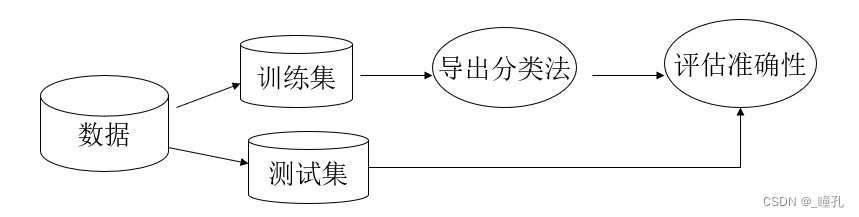
保持(holdout)：

• 随机划分为两个独立的数据集：通常来说，训练集(2/3)，测试集(1/3)
• 变形：随机子选样-holdout方法重复k次
  

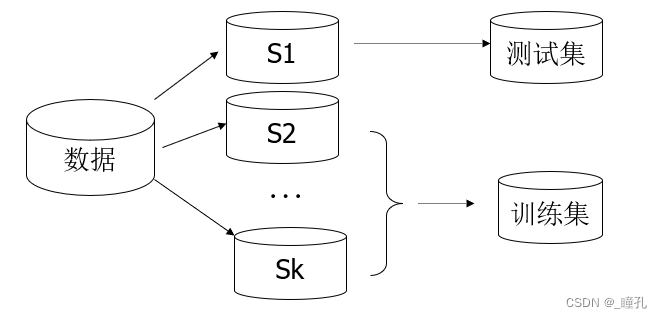
K-次交叉验证(k-fold cross validation)：

• 将数据集分为k个子集
• 用k-1个子集作训练集，1个子集作测试集，然后k次交叉验证
  

数据预处理：

• 数据清理：数据预处理的目的是减少噪音和处理缺失数据
• 数据分析(特征选择)：删除无关的、冗余的属性，选择相关属性
• 数据变换：规范化数据

分类方法的评估：

• 预测精度
• 时间性能
  • 建立模型所花费时间
  • 使用模型所花费时间
• 健壮性：处理噪音和缺失数据的能力
• 空间性能：处理驻磁盘数据库的能力等
• 可理解性：模型给出的结果的可理解性
• 规则的评估：
  • 模型规模大小
  • 分类规则的简洁性

二：决策树

2.1：决策树简介

决策树算法是一种逼近离散函数值的方法。它是一种典型的分类方法，首先对数据进行处理，利用归纳算法生成可读的规则和决策树，然后使用决策对新数据进行分析。本质上决策树是通过一系列规则对数据进行分类的过程。决策树算法是目前应用最为广泛的归纳推理算法之一，在数据挖掘中受到研究者的广泛关注。

决策树分为以下三类。除此之外，还有一些决策树经典改进版算法：Random Forest、GBDT、XGBoost、LightGBM等

• ID3(1986)：由J Ross Quinlan提出，此算法的目的在于减少树的深度。但是忽略了叶子数目的研究。
• C4.5(1993)：在ID3算法的基础上进行了改进，对于预测变量的缺值处理、剪枝技术、派生规则等方面作了较大改进，既适合于分类问题，又适合于回归问题。
• CART(1984)：即分类与回归树算法，可以用来处理涉及连续数据的分类或者回归任务，它和它的变种在当前的工业领域应用非常广泛。

决策树算法构造决策树来发现数据中蕴涵的分类规则．如何构造精度高、规模小的决策树是决策树算法的核心内容。决策树构造可以分两步进行：

• 第一步，决策树的生成：由训练样本集生成决策树的过程。一般情况下，训练样本数据集是根据实际需要有历史的、有一定综合程度的，用于数据分析处理的数据集。
• 第二步，决策树的剪枝：决策树的剪枝是对上一阶段生成的决策树进行检验、校正和修下的过程，主要是用新的样本数据集（称为测试数据集）中的数据校验决策树生成过程中产生的初步规则，将那些影响预衡准确性的分枝剪除。

下图所示为一个典型的决策树模型：员工离职预测模型的简单演示。该决策树首先判断员工满意度是否小于5，答案为“是”则认为该员工会离职，答案为“否”则接着判断其收入是否小于10,000元，答案为“是”则认为该员工会离职，答案为“否”则认为该员工不会离职。

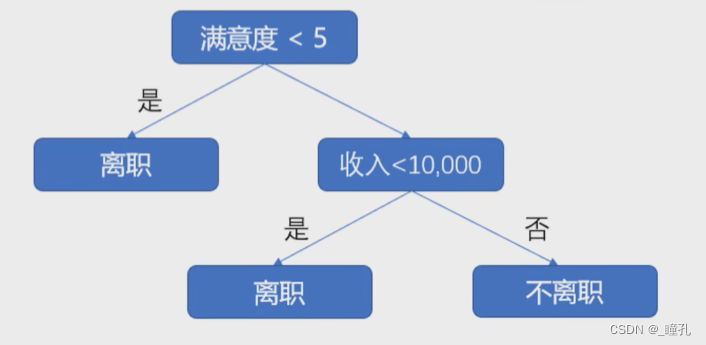
决策树算法的优点如下：

• 分类精度高
• 生成的模式简单
• 对噪声数据有很好的健壮性

2.2：CLS算法

Hunt在66年提出的概念学习系统(ConceptLearning System，CLS）中，定义了基于决策树的学习，CLS算法是最原始的决策树分类算法。

• 该算法接受一组训练实例，构造出决策树
• 决策树从根结点到叶子结点可得到有关概念的一个描述，将类型相同的各个叶子结点所对应的描述合在一起可构成该概念的所有描述
• 构造过程采用的是自上而下的，递归的，分而治之的方法

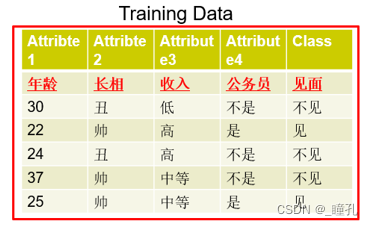
上图数据集构建成决策树如下：

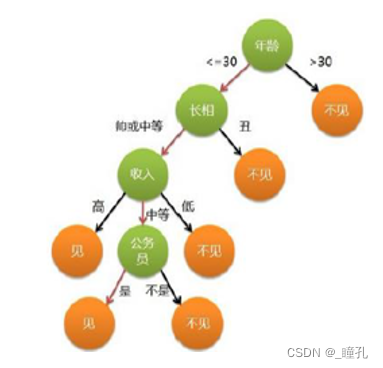
CLS决策树算法的主要步骤如下：

1. T:=所有训练实例集合，产生一个结点T
2. 如果T中所有实例都是正例，则为该结点产生一个“yes”标志，并结束
3. 如果T中所有实例都是反例，则产生一个“no”标志，并结束
4. 否则，选择一个属性X，
   • 假设其所有取值为v₁，v₂.…. ，v_n
   • 则依据这些取值，将T划分为n个子集T₁，T₂，… ，T_n
   • 建T的n个孩子结点T_i，并分别以X=v_i作为从T到T_i的分支标号
5. 对每个T_i，以递归的方式建一棵以T_i为根的子树。

以下是一个例题，对下面数据表，构造出属于buys_computer的分类规则：

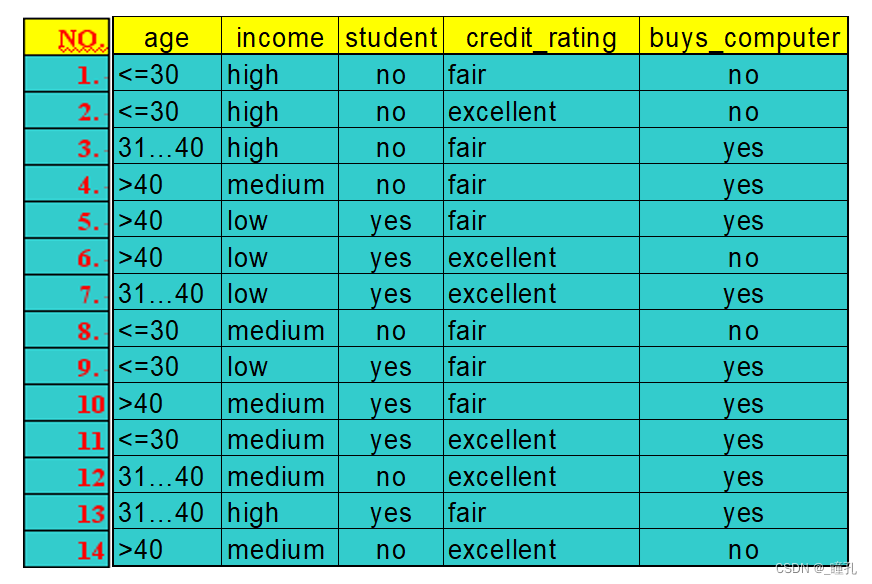
例题答案如下，但显然，这不是唯一的解，还可以有其它形式的决策树。

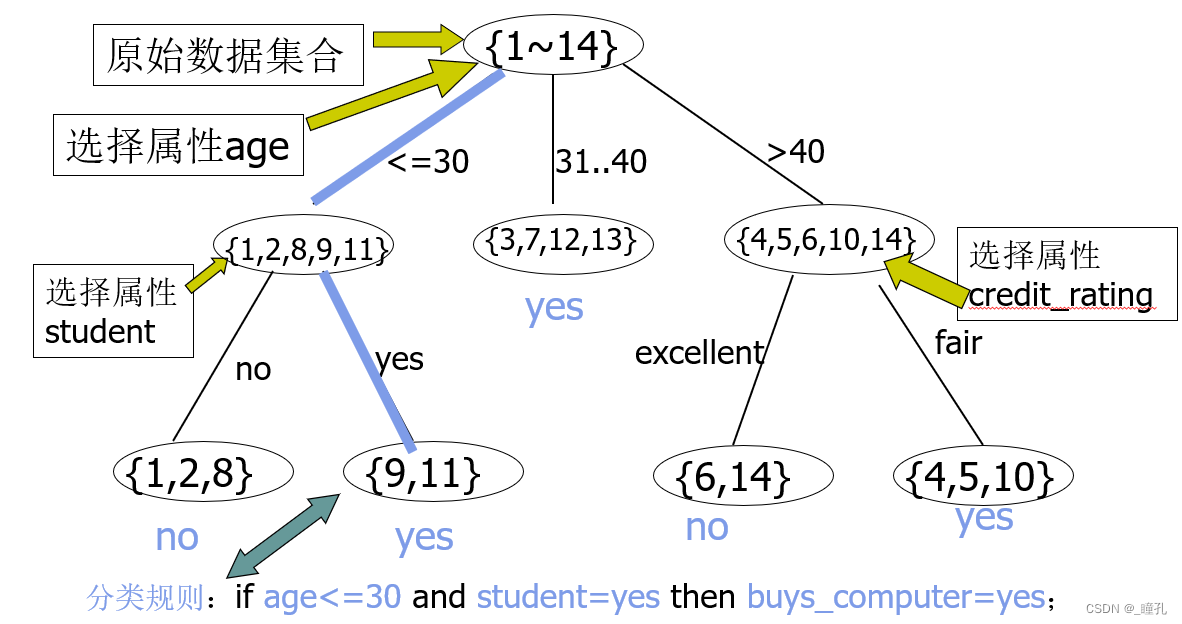
由例题可以看出，这一算法较为简洁、直观，但也存在问题：

• 抗干扰能力弱：噪音数据难免，算法对噪音敏感
• 易受无关属性的影响，导致规则烦琐。
• 受属性选择次序的影响：
  • 各条件属性对分类的影响程度可能存在差异
  • 选择次序得当，将使规则能反映其关系的实质
  • 但如果将影响因素小的在前面展开，将导致规则条件烦琐，不能反映其内在联系。

2.3：ID3算法

学者Quinlan于1986年提出了构造决策树的ID3算法，采用启发式函数计算出属性选择次序。

ID3算法的求解步骤与CLS类似，描述如下：

1. T:=所有训练实例集合，产生一个结点T
2. 如果T中所有实例都属于一个类别，则为该结点产生一个类别标记，并结束
3. 否则，选择具有最高信息增益的属性X
   • 假设其所有取值为v₁，v₂，v_n
   • 则依据这些取值将T划分为n个子集T₁，T₂，…，T_n
   • 建T的n个孩子结点T_i，并分别以X=v_i作为从T到T_i的分支标号
4. 对每个T_i，以递归的方式建一棵以T_i为根的子树

这里就涉及到信息增益的概念了，详情参见下面2.4节

ID3算法的主要思想：

• 对样本的所有特征计算信息增益情况，选择信息增益大的特征来作为决策树的一个结点（信息增益大的特征往往离根结点越近）。
• 当一个特征已经作为划分的依据，再下面递归过程就不在参与了。
• 根结点下面的各个特征按照其取值，样本又可以按照相应特征值进行划分，在当前的样本下利用剩下的特征再次计算信息增益来进一步选择划分的结点，ID3决策树就是这样建立起来的。

2.4：熵与信息增益

熵是信息的期望，也就是计算所有分类包含信息的期望值：

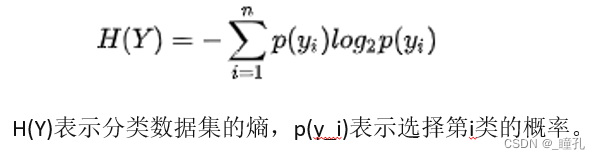
条件熵是在特征X给定条件下，类别Y的条件概率分布的熵对特征X的数学期望

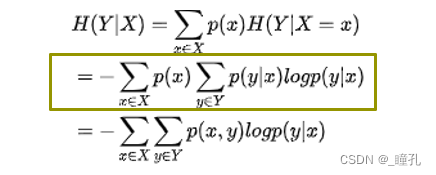
信息增益是指在划分数据集之前之后信息发生的变化，信息增益是熵的减少或者说是数据无序程度的减少。熵减去条件熵就是信息增益。信息增益越大，说明用特征X来划分数据集，信息混乱程度越小。

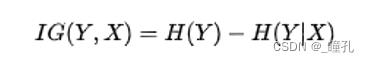
下面的东西我也没看懂，就贴个图吧：

2.4：决策树模型评估

构造的决策树需要用新的数据（测试数据）来检验，获取评价指标，以此作为衡量求解结果的指标，以及作为修正的依据。

训练集合与测试集合的划分典型的划分有：(2:1)、(5:1)、(9:1)

分类的评价指标有：准确率(Accuracy)、召回率(Recall)、精确度(Precision)、F-score、误分类率、时间性能等。

决策树模型的评估方法：

• 扣留测试(Holdout Evaluation)：将被标记的原始数据划分为两个不相交的训练集和测试集，在训练集上归纳分类模型，在测试集上评估该模型的性能
  • 局限性：
    • 当用于训练的被标记样本较少时，这种划分使得训练数据更少，从而影响模型的效果
    • 模型高度依赖划分过程
    • 训练集和测试集不再相互独立
• 交叉验证(Cross-validation)：将数据划分成大小相等的k个子集，每个子集都作为一次测试集，其他的k-1个子集作为训练集，重复k次，其总误差是所有k次运行的误差之和
• 自助法(Bootstrapping)又称“可重复采样”或“有放回采样”，该方法利用有限的样本资料经由多次重复抽样，重新建立起足以代表母体样本分布的新样本。

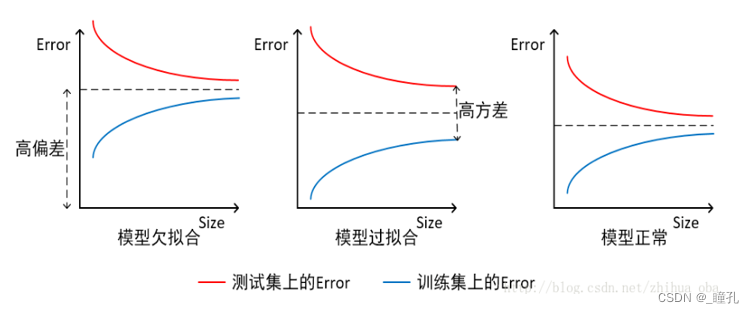
模型的误差，即具有低训练误差和低泛化误差

• 欠拟合：训练误差高，泛化误差高
  • 原因：噪音、不相关数据、样本代表性不足
  • 解决方案：
    • 估计泛化误差：Traning error ≈ generalization error、K-cross validation
    • 结合模型的复杂度：节点个数、最小描述长度
    • 其他方法：重新清洗数据、增加训练样本数量、early stoping/减少迭代次数、添加噪声数据
• 过拟合：训练误差低，泛化误差高
  

2.4：决策树算法的进一步工作

允许处理连续型属性：通过有效的离散化方法，将连续型属性转化为新的离散型属性，再做进一步处理

处理缺失属性值：

• 使用出现最频繁的属性值代替
• 使用每一个属性的可能出现的取值来代替

决策树的优化策略：

• 剪枝
• 优化节点
• 属性选择策略

优化后的决策树具有以下特点：

• 正确分类率高，误分类率低
• 抗噪性能好
• 结构合理
• 规则长度小

对传统决策树的一些改进版本：

• SLIQ：为每一个属性建立一个索引，并且只有当前属性与决策属性存放在内存中
• SPRINT：建立了属性链的数据结构
• PUBLIC：将树的分裂与剪枝相结合，在早期就停止树的生长
• RainForest：将性能方面从一棵决策树的质量评估中除去，建立AVC-list(attribute、value、class label)

2.5：Random Forest算法

随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支――集成学习(Ensemble Learning）方法。

每棵决策树都是一个分类器，对于一个待分类的输入样本，N棵树会有N个分类结果。随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出。

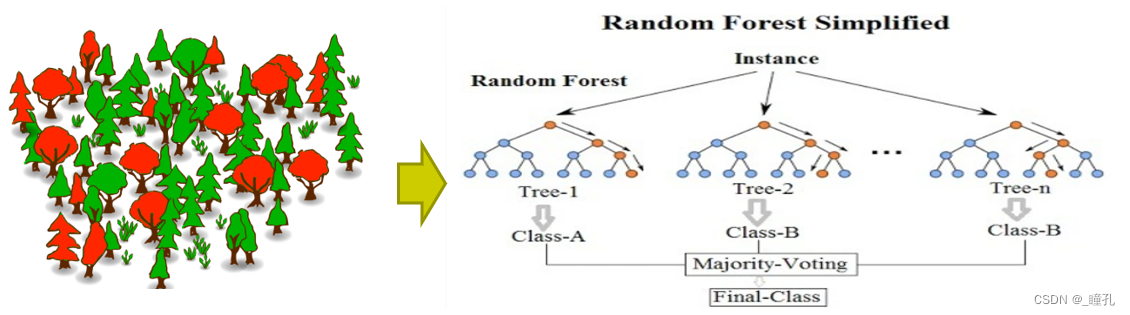
随机森林根据下列步骤建造每一颗树：

1. 用N来表示训练用例（样本）的个数，M表示特征数目。
2. 输入特征数目m，用于确定决策树上一个节点的决策结果，其中m应远小于M。
3. 从N个训练用例（样本）中随机以有放回抽样的方式，取样N次，形成一个训练集，并用未抽到的用例(样本）作预测，评估其误差。
4. 对于每一个节点，随机选择m个特征，决策树上每个节点的决定都是基于这些特征确定的。根据这m个特征，计算其最佳的分裂方式。
5. 每棵树都会完整成长而不会剪枝，这有可能在建完一棵正常树状分类器后会被采用

在第三步中，对于“随机以有放回抽样的方式”做如下说明：

• 有放回抽样的方式：每棵树的训练集都是不同的，而且里面包含重复的训练样本
• 随机抽样：保证样本的随机性，从而保证每颗树的差异性和多样性。如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的。

随机森林分类效果(错误率)与两个因素有关：

• 森林中任意两棵树的相关性：相关性越大，错误率越大
• 森林中每棵树的分类能力：每棵树的分类能力越强，整个森林的错误率越低

如何选择最优的m：m取值太小，树的相关性和分类能力也会相应的降低；m取值太大，两者也会随之增大。(这是随机森林的唯一参数)

三：朴素贝叶斯

3.1：朴素贝叶斯简介

统计学分类方法：预测类成员关系的可能性。例如求解出给定样本属于特定类的概率。

问题描述：

• 假定X是未知类别的样本，H为一个假设(hypothesis)，求P(H|X)
• 对于分类问题，概率P(H|X)表示：当观察到X时，假设H能成立的概率

问题解释：

• P(H|X)：后验概率(posterior probability)，例如：
  • 假设样本域是水果，用颜色和形状来描述
  • 假定：X是红色的、圆的物品；H表示假设：X是苹果
  • 则P(H|X)表示：在看到X是“红色的、圆的”特征后，是苹果的准确程度
• P(H)：先验概率(prior probability)，即H的先验概率；例如，前例中P(H)代表任意给定样本为苹果的概率(无论颜色和形状)
• P(X|H)：后验概率，已知物品是苹果时，具有红色、圆的特征的概率
• P(X)：X的先验概率，水果集中任意一个样本具有红色、圆的特征的概率

贝叶斯定理由英国数学家托马斯·贝叶斯（Thomas Bayes）1763年提出，其内容为：给出训练数据X，假设H，则P(H|X)由贝叶斯公式定义为:

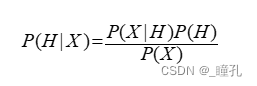
图形方式解释：

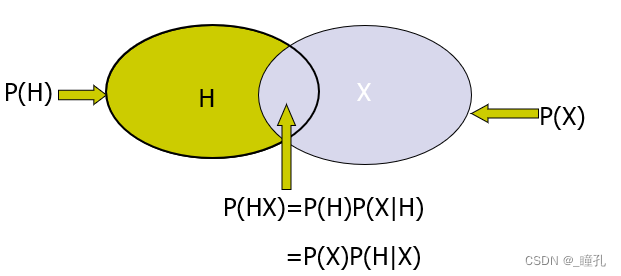
优点：

• 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率
• 实现比较简单
• 对缺失数据不太敏感，常用于文本分类

缺点：朴素贝叶斯会假设各个属性间相互独立，然而实际上，大量的问题中存在关联和依赖，因此失去了准确性。这些问题中存在的大量依赖在朴素贝叶斯分类器模型中不能得到很好的体现。

3.2：分类过程

1. 朴素贝叶斯分类描述

• 假设样本用n维向量(X₁，X₂，…，X_n)表示，对应属性X₁，X₂，…，X_n的取值
• 假定有m个类别C₁，C₂，…，C_m
• 给定对象x，分类算法将预测x属于具有最高后验概率（条件x下）的类。即，若P(C_k |X)>P(C_i|x)（1≤i≤m, i≠k)，则x是C_k类的可能性最大。

2. 公式

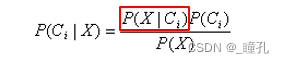
其中分母P(X)对所有类为常量，故只需对各类别计算分子的值。

• 若各类别的先验概率未知，则假定P(C₁)=P(C₂)=…= P(C_m)，因而只需计算最大化的P(X|C_i)即可
• 否则，需计算最大化的P(X|C_i)P(C_i)。

3. 条件独立性假设

条件独立性假设：若属性数较多，则计算P(X|C_i)的开销较大，因而给出类条件独立性假设：给定类别属性，属性间不存在依赖关系，则：

4. 分类

为了对未知的样本X分类，需要对每个类C_i，计算P(X|C_i)P(C_i)，求出值最大的C_i，即为其类别

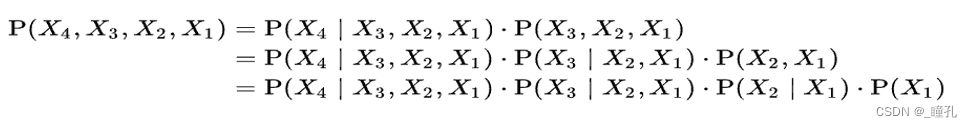
3.3：例题

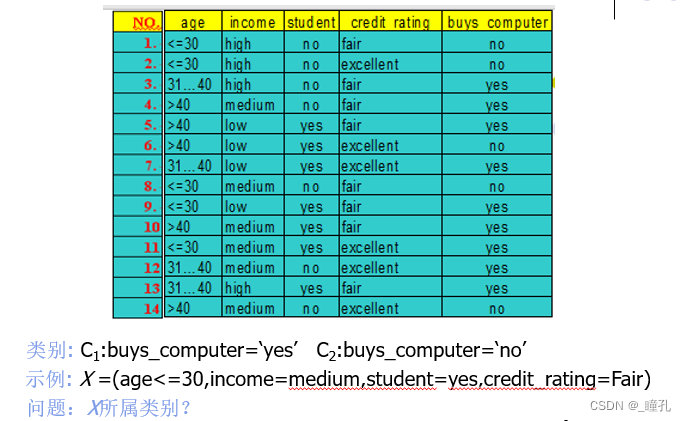
解答：

四：kNN算法

kNN(k-Nearest Neighbor)法即K最邻近法，最初由Cover和Hart于1968年提出，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路非常简单直观：如果一个样本在特征空间中的K个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

kNN分类算法包括以下四个步骤：

1. 准备数据，对数据进行预处理
2. 计算测试样本点（也就是待分类点）到其他每个样本点的距离
3. 对每个距离进行排序，然后选择出距离最小的K个点
4. 对K个点所属的类别进行比较，根据少数服从多数的原则，将测试样本点归入在K个点中占比最高的那一类

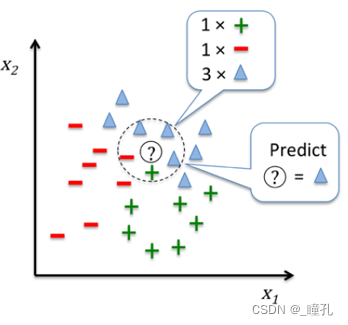
多余维数：邻居间的距离会被不相关的属性影响。为了克服这个问题，可以采用轴延伸或者删除不相关属性。

KNN算法中只有一个超参数k，k值的确定对KNN算法的预测结果有着至关重要的影响。接下来，我们讨论一下k值大小对算法结果的影响以及一般情况下如何选择k值。

如果k值比较小，相当于我们在较小的领域内训练样本对实例进行预测。这时，算法的近似误差（Approximate Error）会比较小，因为只有与输入实例相近的训练样本才会对预测结果起作用。

但是，它也有明显的缺点：算法的估计误差比较大，预测结果会对近邻点十分敏感，也就是说，如果近邻点是噪声点的话，预测就会出错。因此，k值过小容易导致KNN算法的过拟合。

同理，如果k值选择较大的话，距离较远的训练样本也能够对实例预测结果产生影响。这时候，模型相对比较鲁棒，不会因为个别噪声点对最终预测结果产生影响。但是缺点也十分明显：算法的近邻误差会偏大，距离较远的点（与预测实例不相似）也会同样对预测结果产生影响，使得预测结果产生较大偏差，此时模型容易发生欠拟合。

因此，在实际工程实践中，我们一般采用交叉验证的方式选取k值。通过以上分析可知，一般k值选得比较小，我们会在较小范围内选取k值，同时把测试集上准确率最高的那个确定为最终的算法超参数k。

KNN有着非常明显的优点和缺点：

• 优点：精度高、对异常值不敏感、无数据输入假定
• 缺点：计算复杂度高、空间复杂度高
• 适用数据范围：数值型和标称型

在理想化的经典场景中，KNN是非常好用的，但是在非理想化、非经典场景中，KNN这种方法就有点力不从心了。K值究竟选多少？我们需要跟哪些关键属性计算距离？如果我们需要计算的属性很多，对计算机的资源消耗也很大，非常不划算。