---

《Batch Normlization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》 论文详细解读

---

基础知识

一文读懂PCA

面临的挑战

Internal covariate shift (内部协变量偏移)

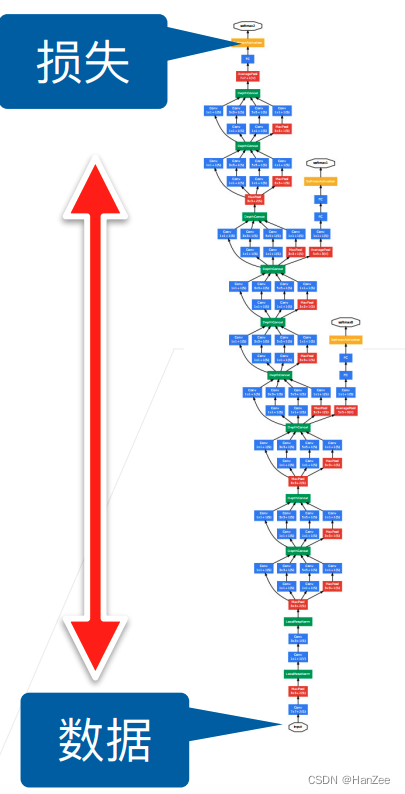
作者把在训练期间参数的改变而导致网络激活分布的改变叫做内部协变量偏移，对此我们有两个版本版本的解释：

1. 如上图所示，前向计算从数据侧到损失侧，反向传播与其相反，函数更新从上到下，随着网络深度的加深，越往下梯度就越小，在学习率固定的情况下，参数更新幅度也就越来越小。靠近损失侧的神经元提取的大多是高层语义信息，这些神经元的权重往往很容易拟合，而靠近数据侧的神经元提取的是底层的纹理、线条等信息，这部分数据权重拟合较慢，因为更新参数会导致分布改变，顶部会不断的去适应底部的分布，这就会导致训练速度很慢。
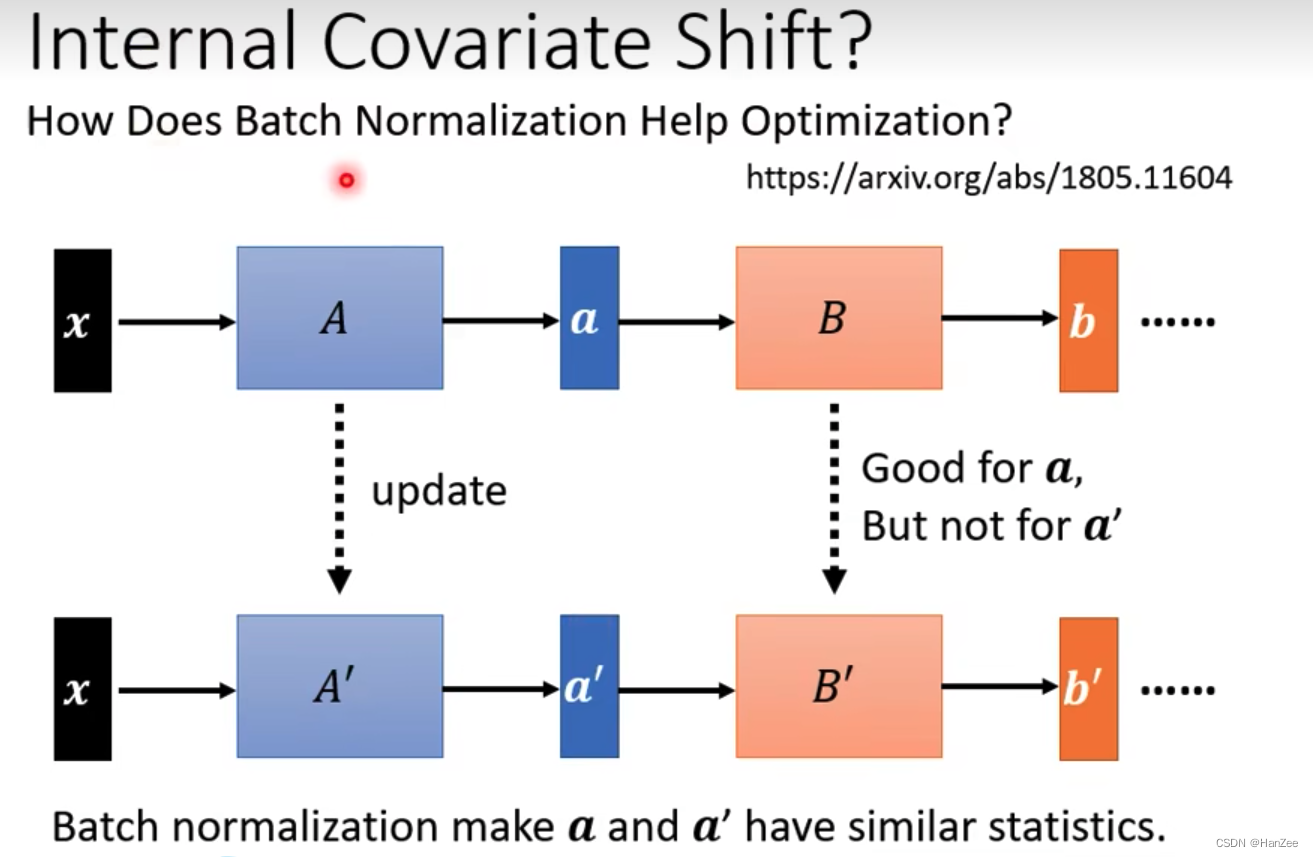
2. 如下图所示，数据x根据参数A输出a（根据链式法则，a也等于函数对B的偏导数），a通过参数B输出b，数据x从左到右前向转播计算损失，之后从后往前计算梯度，我们发现当参数A到A’的时候，参数B也更新到了B’,但是B’的梯度计算是以a为基础的，而此刻a已经变成了a’,也就是说B‘在这个模型中就不是最合适的了，BN的核心思想就是尽量的让a与a’的分布相近，这样可以缓解上面问题所带差距。

解决方案

whiten（白化）

PCA白化

PCA是在对观测数据进行基变换，新的坐标系使各数据维度线性无关，坐标系的重要程度从大到小衰减。

求解过程：

1. 数据标准化（以远点为坐标原点）
2. 求协方差矩阵
3. 对协方差矩阵特征值分解找到最大方差的方向
4. 对数据基变换

其中特征向量，就是最大方差方向，每个特征向量对应的特征值就是这个数据维度的方差。

PCA白化实际上就是在数据通过PCA进行基变换后再把数据进行标准化，让数据每个维度的方差全部为1。
公式推导如下：

符号定义：X：原始数据矩阵 M：原始数据协方差矩阵 设$S^{1/2}$为白化矩阵

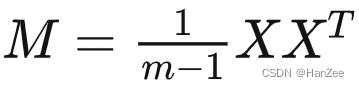
对M特征值分解：

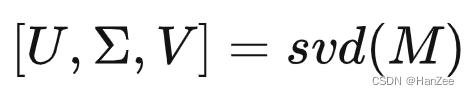
U就是我们要找的变换矩阵，转换数据基坐标：
$$X_{PCA}=UX$$

然后进行白化操作：
lambda为特征值

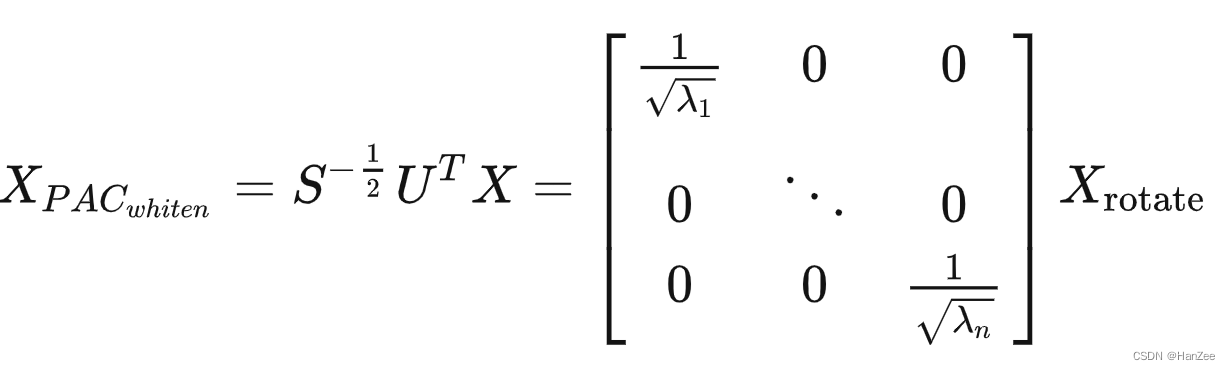
其中有的特征值很小，会造成数值溢出，就给它加上了1个常数项，于是把白化矩阵改为：

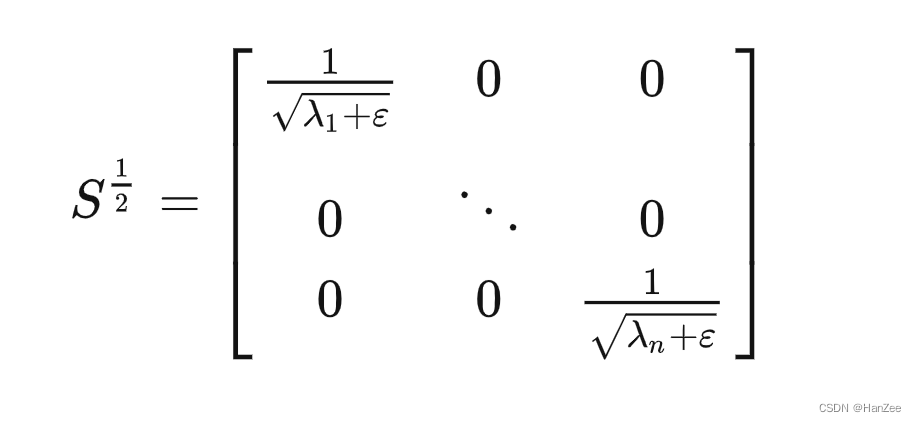
我们发现，白化操作可以让观测数据的方差与均值固定，去除每个维度的相关性。这样确实可以加快模型的收敛，但是也面临着一个问题：
如果忽略了E[x]对b的依赖（也就是反向传播计算梯度的时候考虑均值的影响）

从上面案例中我们发现，更新偏置b前后函数的输出没有改变，也就是损失没有改变，反而b不断增加，这会使模型变得更糟。

我们把归一化操作定义为Norm，如果反向传播不考虑Norm，那么更新的梯度就会与Norm抵消，如果考虑，就会增加很大的计算量。

Batch Normalization

Training

由于白化的计算代价很大，作者提出了简化的版本，从对整个数据集进行归一化改成对每一个Batch的每一层神经元的output归一化来确保均值与方差固定。

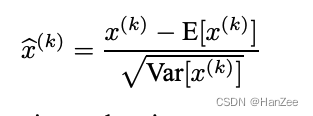
如果把每层的输出固定下来，可能会对网络产生负面的影响，所以我们加入两个可学习的参数：贝塔与伽马使均值与方差变得可以调节。
其中伽马初始化为这一batch对应层输出的方差，贝塔初始化为其均值，从而保证整个network的capacity。（有关capacity的解释：实际上BN可以看作是在原模型上加入的“新操作”，这个新操作很大可能会改变某层原来的输入。当然也可能不改变，不改变的时候就是“还原原来输入”。如此一来，既可以改变同时也可以保持原输入，那么模型的容纳能力（capacity）就提升了。）

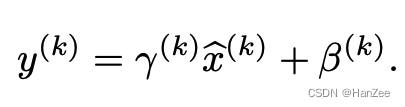
总体流程如下：

反向传播梯度计算公式如下：

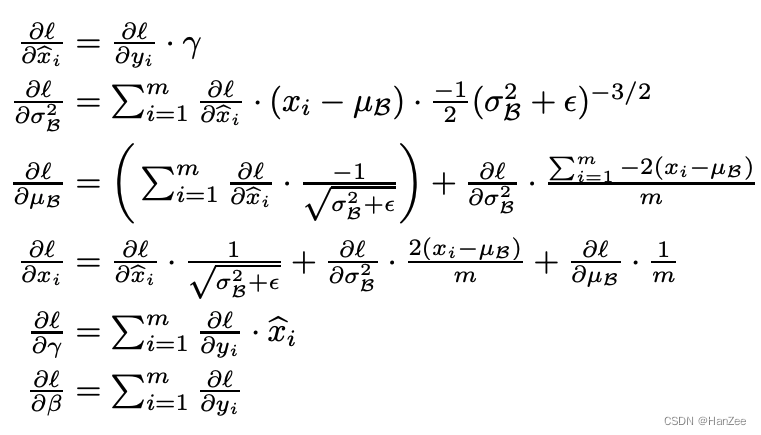
Testing

1. 在训练阶段，我们通过每个batch的数据来计算均值与方差，当在测试阶段，由于一些环境条件的限制，batch一般为1，就不能计算均值与方差了，所以在训练阶段采用指数加权平均的方式来计算所有batch的均值与方差的平均值。
2. 为了使计算更加准确，采用无偏估计。
   

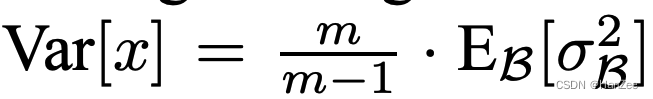
在CNN中的运用

当BN操作应用在卷积层后，作者找到了一个符合卷积神经网络特性的方法，归一化作用在了通道维度上。
我们用代码输出结果展示一下：
用pytorch生成 Batch=2 channel = 3 hw 2 * 2 的特征图：

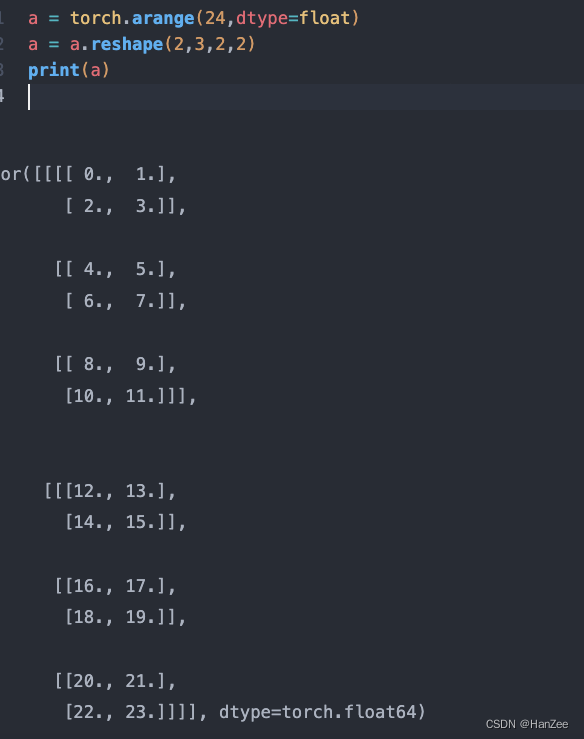
计算均值

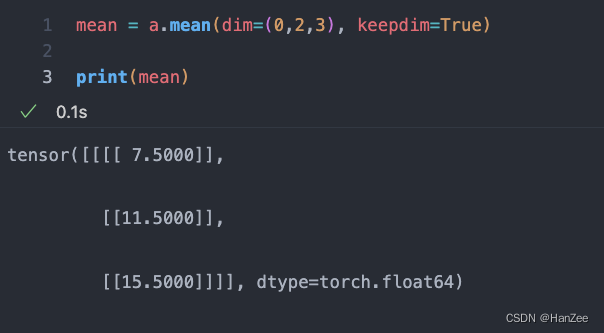
计算举例：
（0+1+2+3+12+13+14+15）/8 = 7.5

总结

1. BN使得每层网络输出分布相对稳定，可以使用更大的学习率加速模型。
2. BN使得模型对网络中的参数不那么敏感，简化调参过程，使得网络学习更加稳定。
3. BN允许网络使用饱和性激活函数（例如sigmoid，tanh等），缓解梯度消失问题。
4. BN具有一定的正则化效果。

代码实现

class BatchNorm(nn.Block):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims, **kwargs):
        super().__init__(**kwargs)
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = self.params.get('gamma', shape=shape, init=init.One())
        self.beta = self.params.get('beta', shape=shape, init=init.Zero())
        # 非模型参数的变量初始化为0和1
        self.moving_mean = np.zeros(shape)
        self.moving_var = np.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.ctx != X.ctx:
            self.moving_mean = self.moving_mean.copyto(X.ctx)
            self.moving_var = self.moving_var.copyto(X.ctx)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma.data(), self.beta.data(), self.moving_mean,
            self.moving_var, eps=1e-12, momentum=0.9)
        return Y