一、什么是支撑向量机？

support vector machine;
使用支撑向量机的思想既可以解决分类问题也可以解决回归问题，先记录分类问题的解决，之后再回归；
关于分类，决策边界有不唯一的问题，通常称为不适定问题。
机器学习很重要的一个特性就是算法的泛化能力，也就是说求出决策边界之后，这个决策边界对于带预测的样本是否是一个好的决策边界，能否非常好的预测未知数据相应的分类结果，要知道对未知数据进行预测分类是机器算法的最终目的；
故而关于决策边界的划分很重要；
我们期望决策边界离蓝色红色都尽可能远，同时还要很好的分别两个类别相应的数据点；
svm对于未来的泛化能力尽可能好的这种考量没有寄望在数据的预处理阶段或者是找到模型之后，再对模型进行正则化这样的方式，而是将对泛化能力的考量放在了算法内部，也就是我们要找到一条决策边界，这条决策边界离我们的分类样本都尽可能的远，直观来看这样的决策边界泛化能力相应的就是好的；这是可以数学严谨证明的，此处不详解；
在这里插入图片描述

svm尝试寻找一个最优的决策边界，距离两个类别的最近的样本最远；
到此为止解决的是线性可分的问题，线性可分就是对于所有样本点来说首先要存在一根直线或者在高维空间中存在一个超平面，可以将这些点划分，这种情况下我们才定义出这个margin；
这样的算法通常又称为是Hard Margin SVM也就是非常严格的切切实实的找到那个最优决策边界；
但是很多现实生活中数据是线性不可分的，那么在这种情况下SVM进一步改进得到Soft Margin SVM这样的算法；
在这里插入图片描述

二、Hard Margin SVM思想逻辑推理

点到直线的距离：

在这里插入图片描述

推论：

在这里插入图片描述

再推：

在这里插入图片描述

换符号替代：

在这里插入图片描述

最大化距离：

在第一行的限定条件下完成下面的最大化式子（有条件的最优化问题）
在这里插入图片描述

三、Soft Margin SVM和SVM正则化

Hard Margin SVM缺点：

在这里插入图片描述

所以我们必须思考一个机制，

对于这个机制来说我们SVM得到的决策边界要能够有一定的容错能力，在一些情况下它应该考虑到可以把一些点进行一些错误的分类，最终要达到的目的是希望结果的泛化能力更高；
那么不再严格要求大于等于1，给它一个宽松量，这就是Soft Margin SVM，当然它也有一个容忍度，要保证容忍度尽量的小即：其中C代表重要程度来平衡两部分，C越大代表容错空间越小，C趋于∞代表逼迫容错空间趋于0。
可以把加入的η项当作本身是一个正则化项，它在避免我们训练出来的模型像一个极端方向发展，把这个模型往回拉一拉；（L1正则化）
在这里插入图片描述
（L2正则化）

四、实际使用SVM

和knn一样，要做数据处理，因为涉及距离，因为数据在不同尺度上可能量纲不同，会非常严重影响到；
在这里插入图片描述

import numpy as np
import matplotlib.pyplot as plt


from sklearn import datasets
iris=datasets.load_iris()
x=iris.data
y=iris.target
x=x[y<2,:2]
y=y[y<2]#先搞二分类问题，也就是y=0=1这两个类别；同时为了方便可视化，特征x只取两个，前两个


plt.scatter(x[y==0,0],x[y==0,1],color='red')#X[y==0,0],是所有编号为0的X坐标;X[y==0,1]是所有编号为0的Y坐标
plt.scatter(x[y==1,0],x[y==1,1],color='blue')
plt.show()


from sklearn.preprocessing import StandardScaler
standarscaler=StandardScaler()
standarscaler.fit(x)
x_standard=standarscaler.transform(x)#数据标准化


from sklearn.svm import LinearSVC
svc=LinearSVC(C=1e9)#1e9 = 1*10^9 = 1000000000设置的非常大本身相当于hardmarginsvm了
svc.fit(x_standard,y)


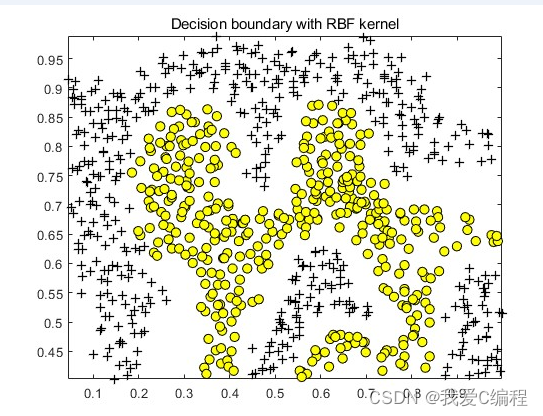
# plot_decision_boundary()函数：绘制模型在二维特征空间的决策边界；
def plot_decision_boundary(model, axis):
    # model：算法模型；
    # axis：区域坐标轴的范围，其中 0,1,2,3 分别对应 x 轴和 y 轴的范围；
    
    # 1）将坐标轴等分为无数的小点，将 x、y 轴分别等分 （坐标轴范围最大值 - 坐标轴范围最小值）*100 份，
    # np.meshgrid()：
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    # np.c_()：
    x_new = np.c_[x0.ravel(), x1.ravel()]
    
    # 2）model.predict(X_new)：将分割出的所有的点，都使用模型预测
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)
    
    # 3）绘制预测结果
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)


plot_decision_boundary(svc, axis=[-3, 3, -3,3])#x和y的范围都是在-3到3之间
plt.scatter(x_standard[y==0, 0], x_standard[y==0, 1])
plt.scatter(x_standard[y==1, 0], x_standard[y==1, 1])
plt.show()

在这里插入图片描述

svc2=LinearSVC(C=0.01)
svc2.fit(x_standard,y)


plot_decision_boundary(svc2, axis=[-3, 3, -3,3])#x和y的范围都是在-3到3之间
plt.scatter(x_standard[y==0, 0], x_standard[y==0, 1])
plt.scatter(x_standard[y==1, 0], x_standard[y==1, 1])
plt.show()


svc.coef_#特征有两个，每个特征都对应一个系数


svc.intercept_#途中只有一根直线只有一个截距

在这里插入图片描述

#改造
# plot_decision_boundary()函数：绘制模型在二维特征空间的决策边界；
def plot_svc_decision_boundary(model, axis):
    # model：算法模型；
    # axis：区域坐标轴的范围，其中 0,1,2,3 分别对应 x 轴和 y 轴的范围；
    
    # 1）将坐标轴等分为无数的小点，将 x、y 轴分别等分 （坐标轴范围最大值 - 坐标轴范围最小值）*100 份，
    # np.meshgrid()：
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    # np.c_()：
    x_new = np.c_[x0.ravel(), x1.ravel()]
    
    # 2）model.predict(X_new)：将分割出的所有的点，都使用模型预测
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)
    
    # 3）绘制预测结果
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
    w=model.coef_[0]
    b=model.intercept_[0]
    #目前图中线为w0*x0+w1*x1+b=0
    #改写：x1=-w0/w1*x0-b/w1
    plot_x=np.linspace(axis[0],axis[1],200)#x的范围从axis0到1之间取200个点
    up_y=-w[0]/w[1]*plot_x-b/w[1]+1/w[1]
    down_y=-w[0]/w[1]*plot_x-b/w[1]-1/w[1]
    #将plot_x,up_y以折线图的方式表现出来；plot_x,down_y以折线图的方式表现出来
    #此处还有一个需要注意的地方就是此时求出的up_y和down_y有可能已经超过了我们传给这个函数中坐标axis规定的范围，这里要在做一个简单的过滤
    up_index=(up_y>=axis[2])&(up_y<=axis[3])
    down_index=(down_y>=axis[2])&(down_y<=axis[3])
    plt.plot(plot_x[up_index],up_y[up_index],color='yellow')#plot_x要在up_index这个范围中
    plt.plot(plot_x[down_index],down_y[down_index],color='yellow')

plot_svc_decision_boundary(svc, axis=[-3, 3, -3,3])#x和y的范围都是在-3到3之间
plt.scatter(x_standard[y==0, 0], x_standard[y==0, 1])
plt.scatter(x_standard[y==1, 0], x_standard[y==1, 1])
plt.show()

在这里插入图片描述

plot_svc_decision_boundary(svc2, axis=[-3, 3, -3,3])#x和y的范围都是在-3到3之间
plt.scatter(x_standard[y==0, 0], x_standard[y==0, 1])
plt.scatter(x_standard[y==1, 0], x_standard[y==1, 1])
plt.show()